Те, кто часто путешествуют самолетами, любят просить место у прохода. Ведь если сидеть у прохода, можно встать и прогуляться, не тревожа своих соседей.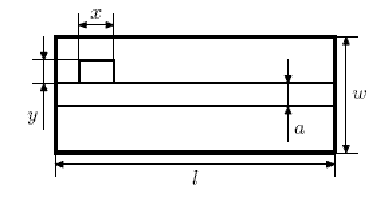
Компания «Аэротрам» готовит к производству новый самолет «T-239-n». Перед инженерами встала задача спланировать организацию салона, чтобы как можно больше мест было у прохода. Будем использовать следующую упрощенную математическую модель салона самолета. В горизонтальном сечении салон представляет собой прямоугольник длиной l и шириной w сантиметров. Кресло представляет собой прямоугольник размером x на y сантиметров и должно быть расположено в салоне так, чтобы его сторона длиной x была параллельна стороне салона длиной l. Проход представляет собой полосу шириной a, параллельную стороне салона длиной l. Проход идет вдоль всего салона.
В салоне требуется разместить n кресел. Помогите инженерам компании выяснить, как организовать салон, чтобы максимальное количество кресел было расположено у прохода. В салоне необходимо сделать хотя бы один проход. Кресло считается расположенным у прохода, если оно имеет хотя бы одну общую сторону с проходом.
Входной файл содержит шесть целых чисел: n, l, w, x, y и a (1 ≤ n ≤ 10000, 1 ≤ l,w,x,y,a ≤ 104).
Если разместить n кресел в салоне так, чтобы был хотя бы один проход, невозможно, выведите в выходной файл единственное число −1 . Иначе выведите максимальное количество кресел, которое можно разместить у прохода.
Комментарий к примерам тестов.
В первом примере оптимально расположить кресла, например, следующим образом:
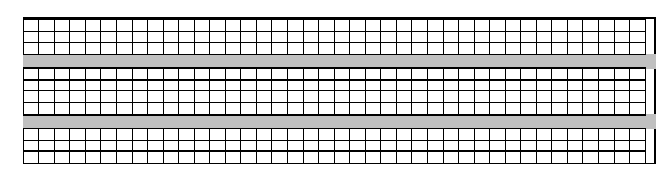
400 3250 750 80 60 70
160
450 3250 750 80 60 70
-1
Власти Флатландии решили построить новый мост через реку Нижний Флат, протекающую с юга на север через территорию страны. В связи с финансовым кризисом средства строителей существенно ограничены, поэтому решено было построить мост минимальной возможной длины. 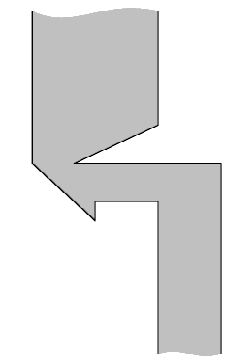
Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX с запада на восток. Берега реки представляют собой ломаные, бесконечные в обе стороны. Левый берег начинается лучом, направленным на юг из точки (x1,1,y1,1), продолжается отрезками (x1,1,y1,1) − (x1,2,y1,2), (x1,2,y1,2)− (x1,3,y1,3), ..., (x1,m−1,y1,m−1) − (x1,m,y1,m) и заканчивается лучом, направленным на север из точки (x1,m,y,m).
Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2,1,y2,1), продолжается отрезками (x2,1,y2,1) − (x2,2,y2,2), (x2,2,y2,2) − (x2,3,y2,3), ..., (x2,n−1,y2,n−1) − (x2,n,y2,n) и заканчивается лучом, направленным на север из точки (x2,n,y2).
Помогите руководству Флатландии выяснить, мост какой минимальной длины можно построить.
Первая строка входного файла содержит целое число m (2 ≤ m ≤ 100). Следующие m строк содержат по два целых числа координаты вершин ломаной левого берега: x1,1, y1,1, x1,2,y1,2, ...,x1,m, y1,m.
Следующая строка входного файла содержит целое число n (2 ≤ n ≤ 100). Следующие n строк содержат по два целых числа координаты вершин ломаной правого берега: x2,1, y2,1, x2,2, y2,2, ..., x2,n, y2,n.
Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине
Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.
Оптимальное положение моста показано на следующем рисунке:
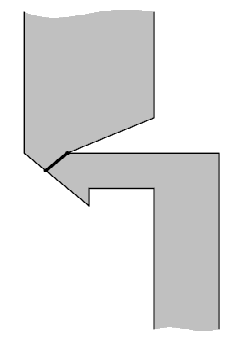
4 6 1 3 1 3 0 0 3 3 9 3 2 3 6 5
1.4142135623730951
В теории кодирования часто используют беспрефиксные коды наборы слов, ни одно из которых не является префиксом (Слово α называется префиксом слова β, если α получается из β удалением нуля или более символов в конце. Например, слова, a, ab и aba являются префиксами слова aba) другого. Например, набор слов aba, aa и bac является беспрефиксным кодом, а набор abac, aba, ba нет, поскольку слово aba является префиксом слова abac.
Профессор Дешифро работает в лаборатории исследования бесполезной информации и изучает свое новое изобретение почти беспрефиксные коды. Набор слов называется почти беспрефиксным кодом уровня k, если наибольший общий префикс двух любых слов из набора не превышает по длине k. Например, набор abac, abс, ba является почти беспрефиксным кодом уровня 2, а набор abac , abab, ba нет, поскольку наибольший общий префикс слов abac и abab имеет длину 3.
Очередная задача, которую профессор Дешифро поставил своим лаборантам, заключается в следующем: по заданному набору слов и числу k требуется выбрать из заданных слов максимальный набор, который является почти беспрефиксным кодом уровня k. Вам, как младшему лаборанту, поручили написать соответствующую программу.
Первая строка входного файла содержит два целых числа: n и k количество слов в заданном наборе и уровень почти беспрефиксного кода, который требуется построить (1 ≤ n ≤ 100000, 0 ≤ k ≤ 200). Следующие n строк содержат по одному слову. Слова состоят из строчных букв латинского алфавита. Длина каждого слова от 1 до 200 символов. Суммарная длина всех слов не превышает 106. Все слова различны.
На первой строке выходного файла выведите одно число m - максимальное количество слов, которые можно выбрать из заданного набора, чтобы они образовывали почти беспрефиксный код уровня k. Следующие m строк должны содержать выбранные слова.
6 2 aba bacaba abacaba baca abac caba
3 aba baca caba
Недавно на кружке по программированию Петя узнал об обходе в глубину. Обход в глубину используется во многих алгоритмах на графах. Петя сразу же реализовал обход в глубину на своих любимых языках программирования Паскале и Си.
| Паскаль | Си |
| var a: array [1..maxn, 1..maxn] of boolean; visited: array [1..maxn] of boolean;
procedure dfs(v: integer); var i: integer; begin writeln(v); visited[v] := true; for i := 1 to n do begin if a[v][i] and not visited[i] then begin dfs(i); writeln(v); end; end; end;
procedure graph_dfs; var i: integer; begin for i := 1 to n do if not visited[i] then dfs(i); end; | int a[maxn + 1][maxn + 1]; int visited[maxn + 1];
void dfs(int v) { printf("%d\n", v); visited[v] = 1; for (int i = 1; i <= n; i++) { if ((a[v][i] != 0) && (visited[i] == 0)) { dfs(i); printf("%d\n", v); } } }
void graph_dfs() { for (int i = 1; i <= n; i++) { if (visited[i] == 0) { dfs(i); } } } |
Петина программа хранит граф с использованием матрицы смежности в массиве a (вершины графа пронумерованы от 1 до n). В массиве visited помечается, в каких вершинах обход в глубину уже побывал.
Петя запустил процедуру graph_dfs для некоторого неориентированного графа G с n вершинами и сохранил ее вывод. А вот сам граф потерялся. Теперь Пете интересно, какое максимальное количество ребер могло быть в графе G. Помогите ему выяснить это!
Первая строка входного файла содержит два целых числа: n и l количество вершин в графе и количество чисел в выведенной последовательности (1 ≤ n ≤ 300, 1 ≤ l ≤ 2n − 1). Следующие l строк по одному числу вывод Петиной программы. Гарантируется, что существует хотя бы один граф, запуск программы Пети на котором приводит к приведенному во входном файле выводу.
На первой строке выходного файла выведите одно число m максимальное возможное количество ребер в графе.
Следующие m строк должны содержать по два целых числа номера вершин, соединенных ребрами. В графе не должно быть петель и кратных ребер.
6 10 1 2 3 2 4 2 1 5 6 5
6 1 2 1 3 1 4 2 3 2 4 5 6
В одной далекой восточной стране до сих пор по пустыням ходят караваны верблюдов, с помощью которых купцы перевозят пряности, драгоценности и дорогие ткани. Разумеется, основная цель купцов состоит в том, чтобы подороже продать имеющийся у них товар. Недавно один из караванов прибыл во дворец одного могущественного шаха.
Купцы хотят продать шаху n драгоценных камней, которые они привезли с собой. Для этого они выкладывают их перед шахом в ряд, после чего шах оценивает эти камни и принимает решение о том, купит он их или нет. Видов драгоценных камней на Востоке известно не очень много всего 26, поэтому мы будем обозначать виды камней с помощью строчных букв латинского алфавита. Шах обычно оценивает камни следующим образом. Он заранее определил несколько упорядоченных пар типов камней: (\(a_1\), \(b_1\)), (\(a_2\), \(b_2\)), ..., (\(a_k\), \(b_k\)). Эти пары он называет красивыми, их множество мы обозначим как P. Теперь представим ряд камней, которые продают купцы, в виде строки S длины n из строчных букв латинского алфавита. Шах считает число таких пар (i,j), что 1 ≤ i < j ≤ n, а камни \(S_i\) и \(S_j\) образуют красивую пару, то есть существует такое число 1 ≤ q ≤ k, что \(S_i = a_q\) и \(S_j = b_q\).
Если число таких пар оказывается достаточно большим, то шах покупает все камни. Однако в этот раз купцы привезли настолько много камней, что шах не может посчитать это число. Поэтому он вызвал своего визиря и поручил ему этот подсчет. Напишите программу, которая находит ответ на эту задачу.
Первая строка входного файла содержит целые числа n и k (1 ≤ n ≤ 100000, 1 ≤ k ≤ 676) число камней, которые привезли купцы и число пар, которые шах считает красивыми. Вторая строка входного файла содержит строку S, описывающую типы камней, которые привезли купцы.
Далее следуют k строк, каждая из которых содержит две строчных буквы латинского алфавита и описывает одну из красивых пар камней.
В выходной файл выведите ответ на задачу — количество пар, которое должен найти визирь.
7 1 abacaba aa
6
7 3 abacaba ab ac bb
7