Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 175 176 177 178 179 180 181 >> Отображать по:
#1141
Нечестная игра
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Есть число N. Играют два игрока, первый может отнять от числа любое число от 1 до K. На каждом следующем ходу можно отнять любое число от 1 до <предыдущий ход>+1. Проигрывает тот, кто возьмет последнюю спичку. Требуется вывести все первые ходы, приводящие к победе.

Петя придумал новую игру. На стол кладется кучка из N спичек, и затем Петя с Ваней по очереди берут спички из кучки. Первым берет Петя, ему разрешается взять от 1 до K спичек. Затем игрок может взять любое количество спичек, не более чем на 1 превышающее то количество, которое взял игрок перед ним (можно взять меньше или столько же, но обязательно хотя бы одну). Например, если N = 10, K = 5, то на первом ходу Петя может взять 1, 2, 3, 4 или 5 спичек, если Петя возьмет 3, то на следующем ходу Ваня может взять 1, 2, 3 или 4, и если Ваня возьмет 1, то Петя затем может взять 1 или 2, и т. д. Проигрывает тот, кто возьмет последнюю спичку.

Теперь Петя хочет рассчитать какое количество спичек он должен взять на первом ходу, чтобы выиграть при любой игре Вани. Помогите ему.

Входные данные

На первой строке входного файла находятся числа N и K, разделенные пробелом. (1 ≤ K ≤ N ≤ 200).

Выходные данные

Выведите в выходной файл все такие X, что, взяв на первом ходу X спичек, Петя выиграет. Если таких X не существует, выведите в выходной файл единственное число - 0. Числа следует разделять пробелами и выводить в порядке возрастания.

Примеры
Входные данные
2 2
Выходные данные
1
Входные данные
5 4
Выходные данные
1 4
#1150
Таблица
  

Рассмотрим прямоугольную таблицу размером n m. Занумеруем строки таблицы числами от 1 до n, а столбцы – числами от 1 до m. Будем такую таблицу последовательно заполнять числами следующим образом.

Обозначим через aij число, стоящее на пересечении i-ой строки и j-ого столбца. Первая строка таблицы заполняется заданными числами – a11, a12, …, a1m. Затем заполняются строки с номерами от 2 до n. Число aij вычисляется как сумма всех чисел таблицы, находящихся в «треугольнике» над элементом aij. Все вычисления при этом выполняются по модулю r.






























 

 

ai,j

















Более точно, значение aij вычисляется по следующей формуле:

 

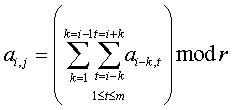
Например, если таблица состоит из трех строк и четырех столбцов, и первая строка состоит из чисел 2,3,4,5, а r = 40 то для этих исходных данных таблица будет выглядеть следующим образом (взятие по модулю показано только там, где оно приводит к изменению числа):

2

3

4

5

5 = 2 + 3

9 = 2 + 3 + 4

12 = 3 + 4 + 5

9 = 4 + 5

23 = 2 + 3 + 4 + 5 + 9

0 = (2 + 3 + 4 + 5 + 5 + 9 + 12) mod 40 = 40 mod 40

4 = (2 + 3 + 4 + 5 + 9 + 12 + 9) mod 40 = 44 mod 40

33 = 3 + 4 + 5 + 12 + 9

Требуется написать программу, которая по заданной первой строке таблицы (a11, a12, …, a1m), вычисляет последнюю строку, как описано выше.

Входные данные

Первая строка входного файла содержит числа n, m и r (2 ≤ n, m ≤ 2000, 2 ≤ r ≤ 109) – число строк и столбцов таблицы соответственно, а так же число, по модулю которого надо посчитать ответ. Следующая строка содержит m целых чисел – первую строку таблицы: a11, a12, …, a1m. Все a1i неотрицательны и не превосходят 109.

Выходные данные

В первой строке выходного файла необходимо вывести m чисел – последнюю строку таблицы: an1, an2, …, anm.

Примеры
Входные данные
2 3 10
1 2 3
Выходные данные
3 6 5
Входные данные
3 3 10
1 1 1
Выходные данные
8 0 8
Входные данные
3 4 40
2 3 4 5
Выходные данные
23 0 4 33
#1151
Гомотетия
  

Гомотетией с центром O и коэффициентом k 0 называют преобразование плоскости, при котором точка O переходит сама в себя, а любая точка X O – в такую точку Y, что:

  • Y лежит на прямой OX;
  • OY = |k|OX;
  • при k >0 Y лежит на луче OX, при k <0 Y лежит на продолжении луча OX за точку O.

Требуется написать программу, которая по координатам вершин двух различных простых N-угольников определяет, существует ли гомотетия, переводящая первый многоугольник во второй и, если существует, вычисляет ее центр и коэффициент.

Входные данные

В первой строке входного файла содержится целое число n (3 ≤ n ≤ 1000) – количество вершин в каждом многоугольнике

В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин первого многоугольника в порядке обхода против часовой стрелки.

В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин второго многоугольника в порядке обхода против часовой стрелки.

Выходные данные

Если существует гомотетия, которая переводит первый многоугольник во второй, то необходимо вывести в первой строке выходного файла слово «YES», а во второй строке – три вещественных числа – координаты центра гомотетии и ее коэффициент, которые вычисляются с точностью не менее 10-5. Если искомой гомотетии не существует, необходимо вывести в выходной файл слово «NO».

Примеры
Входные данные
3
-1 1
1 1
1 5
1 9
-3 1
1 1
Выходные данные
YES
1.0 1.0 2.0
Входные данные
3
-1 1
1 1
1 5
1 1
0 0
1 0
Выходные данные
NO
#1152
Информатизация садоводства
  

Дачный участок Степана Петровича имеет форму прямоугольника размером a × b. На участке имеется n построек, причем основание каждой постройки — прямоугольник со сторонами, параллельными сторонам участка.

Вдохновленный успехами соседей, Степан Петрович хочет посадить на своем участке m видов плодовых культур (участок Степана Петровича находится в северной местности, поэтому m = 1 или m = 2). Для каждого вида растений Степан Петрович хочет выделить отдельную прямоугольную грядку со сторонами, параллельными сторонам участка. Само собой, грядки не могут занимать территорию, занятую постройками или другими грядками.

Степан Петрович хочет расположить грядки таким образом, чтобы их суммарная площадь была максимальной. Грядки не должны пересекаться, но могут касаться друг друга.


грядка №1



дом

сарай

грядка №2


Требуется написать программу, которая по заданным размерам участка и координатам построек определяет оптимальное расположение планируемых грядок.

Входные данные

В первой строке входного файла содержатся два целых числа n и m (0 ≤ n ≤ 10; 1 ≤ m ≤ 2).

Во второй строке содержатся два целых числа a и b (1 ≤ a, b ≤ 10000).

Далее следуют n строк, каждая из которых содержит четыре целых числа xi,1 , yi,1, xi,2, yi,2 –координаты двух противоположных углов постройки (0 xi,1 < xi,2 a, 0 yi,1 < yi,2   b). Различные постройки не могут пересекаться, но могут касаться друг друга.

Выходные данные

В выходной файл необходимо вывести m строк, каждая из которых содержит координаты двух противоположных углов предполагаемой грядки. Координаты должны быть целыми (всегда можно добиться максимальной суммарной площади грядок, располагая их в прямоугольниках с целыми координатами).

В случае, если в вашем решении Степану Петровичу следует расположить менее m грядок, необходимо вывести для грядок, которые не следует сажать, строку «0 0 0 0» (см. второй пример ниже).

Примеры
Входные данные
2 2
7 5
4 2 6 4
0 1 2 2
Выходные данные
0 2 4 5
2 0 7 2
Входные данные
3 2
4 4
0 0 4 1
0 1 1 4
3 1 4 4
Выходные данные
1 1 3 4
0 0 0 0
#1153
Две строки
  

Циклическим сдвигом строки s0s1…sn-1 на k позиций назовем строку sksk+1…sns1..sk-1. Например, циклическим сдвигом строки «abcde» на две позиции является строка «cdeab». В этой задаче далее будут рассматриваться только строки, состоящие из десятичных цифр от 0 до 9. Произвольной такой строке, первый символ которой не является нулем, можно сопоставить число, десятичной записью которого она является. Строкам, которые начинаются с нуля, никакое число сопоставляться не будет. Например, строке 123 сопоставляется число сто двадцать три, а строке 0123 не сопоставляется никакое число.

Пусть заданы две строки: s и t. Обозначим как S набор всех циклических сдвигов строки s, а как T – набор всех циклических сдвигов строки t. Например, если s = «1234», то S содержит строки «1234», «2341», «3412», «4123». Обозначим также как NUM(A) набор чисел, соответствующих строкам из набора  A.

Требуется написать программу, которая по строкам s и t определит, максимальное число, представимое в виде разности (x – y), где x принадлежит NUM(S), а y принадлежит NUM(T). Например, если s = «25», t = «12», то NUM(S) содержит числа 25 и 52, NUM(T) – числа 12 и 21; их попарными разностями будут: 25 – 12 = 13, 25 – 21 = 4, 52 – 12 = 40, 52 – 21 = 31. Из этих разностей максимальным числом является 40.

Входные данные

Первая строка входного файла содержит строку s, вторая строка входного файла – строку t. Обе строки непустые. Они содержат только цифры, из которых хотя бы одна не является нулем. Строки имеют длину не более 3000 символов.

Выходные данные

В выходной файл выведите искомое число без ведущих нулей.

Примеры
Входные данные
25
12
Выходные данные
40
Входные данные
100
1
Выходные данные
99
Страница: << 175 176 177 178 179 180 181 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест