Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 195 196 197 198 199 200 201 >> Отображать по:
#1344
Многоугольники
  
ограничение по времени на тест
0.1 second;
ограничение по памяти на тест
64 megabytes

На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:

  • никакие два многоугольника не имеют общих точек;
  • для каждого i –го многоугольника существует Pi многоугольников, внутри которых он находится, и N-1-Pi многоугольников, которые находятся внутри его, 0 ≤Pi≤N-1.

Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.

Входные данные

Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число Ci — количество вершин многоугольника, 3≤Ci≤20. Последующие Ci пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.

Выходные данные

Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть Pi — количество многоугольников, внутри которых находится i–ый многоугольник.

Примеры
Входные данные
3
3 -2 1 8 9 12 1
3 7 5 6 3 7 4
4 4 3 7 7 9 3 1 2
Выходные данные
0 2 1
#1346
ВТО
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

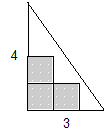Территория Великой Треугольной Области (ВТО) представляет собой прямоугольный треугольник. Длины его катетов равны M и N государственных единиц длины (ГЕД). Правительство ВТО решило покрыть как можно большую часть территории области квадратными плитами размером 11 ГЕД. Плиты должны плотно прилегать друг к другу и к катетам ВТО. Разрезать плиты нельзя.

Согласно межгосударственным соглашениям, правительство ВТО не имеет права покрыть частью своей плиты чужую территорию. Производитель поставляет плиты только контейнерными партиями — по P плит. Правительство заказывает столько контейнеров, сколько необходимо для реализации проекта.

Заведующий центральным складом, узнав про проект, решил, что его интересует коли­чество плит, которые останутся на складе из последнего контейнера после покрытия территории ВТО.

Напишите программу, которая по длинам катетов ВТО и вместимости контейнера находит количество плит, которые останутся на складе после осуществления проекта.

Входные данные

Единственная строка входного файла содержит три целых числа: M, N (2≤M, N≤2 000 000 000) и P (100≤P≤10 000).

Выходные данные

Единственная строка выходного файла должна содержать целое число — количество неиспользованных плит из последнего контейнера.

Примеры
Входные данные
4 3 100
Выходные данные
97
#1349
Постройте квадрат
  

Заданы координаты точки A (xa, ya) и точки B (xb, yb). Найдите еще две точки C и D, такие что ACBD – квадрат, причем AB – его диагональ.

Входные данные

С клавиатуры вводятся xa, ya, xb и yb, гарантируется, что точки A и B не совпадают. Исходные данные являются целыми числами, по модулю не превышающими 1000.

Выходные данные

Результат: в первой строке выведите координаты точки C, во второй – координаты точки D; точки можно выводить в произвольном порядке. Результаты необходимо вывести с точностью до пятого знака после запятой.

Комментарий к примеру тестов

Ответ: 1 1 0 0 также будет правильным

Примеры
Входные данные
1 0 0 1
Выходные данные
1 0 0 1
#1350
Постройте отражение
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Заданы коэффициенты уравнения прямой ax + by + c = 0 и координаты точки A (xa, ya). Найдите точку B, которая является отражением точки A относительно заданной прямой.

Входные данные

В начале с клавиатуры вводятся коэффициенты уравнения прямой a, b, c, затем координаты точки A. Исходные данные являются целыми числами, по модулю не превышающими 1000

Выходные данные

Выведите координаты точки B с точностью до пятого знака после запятой.

Примеры
Входные данные
1 0 0 3 1
Выходные данные
-3.0000000 1.0000000
Входные данные
1 -1 0 1 0
Выходные данные
-0.0000000 1.0000000
#1351
Увеличьте треугольник
  

Даны координаты вершин треугольника A (xa, ya), B(xb, yb), C(xc, yc) и коэффициент увеличения k. Найдите такие точки B’ и C’, что стороны треугольника AB’C’ в k раз больше сторон треугольника ABC и при этом точка B’ лежит на луче AB, а точка C’ лежит на луче AC.

Входные данные

Сначала с клавиатуры вводятся координаты точек A, B и С, затем коэффициент увеличения k (k -положительное число).

Исходные данные являются целыми числами, по модулю не превышающими 1000

Выходные данные

В первой строке выведите координаты точки B’, во второй C’. Результаты необходимо вывести с точностью до пятого знака после запятой.

Примеры
Входные данные
1 1 1 2 2 1 3
Выходные данные
1 4
4 1
Страница: << 195 196 197 198 199 200 201 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест