Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 226 227 228 229 230 231 232 >> Отображать по:
#1684
Радиолокация
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вводится новый авиарейс между городами \(A\) и \(B\). Самолет будет лететь строго по прямой, соединяющей эти города. На протяжении всего пути необходимо, чтобы за самолетом могли наблюдать с земли при помощи радаров. Однако, радиус действия радаров ограничен, и равен \(R\). Хуже того, радарные станции имеются только в определенных точках (например, других населенных пунктах). Руководство авиакомпании желает выяснить: можно ли следить за самолетом на протяжении всего пути из \(A\) в \(B\). Если это возможно, то каким минимальным количеством уже имеющихся радаров можно для этого обойтись. Самолет, находящийся на границе действия радара является видимым, то есть если расстояние от радара до самолета точно равно \(R\), то считается что радар еще действует.

Входные данные

сначала вводятся координаты точек \(A\) и \(B\) (целые числа, по модулю не превышают 1000), затем вводится число \(N\) (натуральное, не превышает 20) – количество уже построенных радаров, затем следует число \(R\) – радиус действия радара (натуральное, не превышает 1000). Затем вводится \(N\) пар чисел – координаты уже построенных радаров (целые, по модулю не превышают 1000). Наличие радаров в городах \(A\) и \(B\) возможно, но необязательно.

Выходные данные

выведите минимальное количество радаров, которое надо задействовать для сопровождения самолета на всем пути. Если сопровождение имеющимися средствами невозможно – выведите число -1.

Примеры
Входные данные
0 0 1 1
1 1
5 5
Выходные данные
-1
Входные данные
0 0 10 0
3 5
0 0
5 0
10 0
Выходные данные
1
#1692
Вспомогательные вопросы жизни, вселенной и всего такого
  

Как вы знаете, ученые сформулировали главный вопрос жизни, вселенной и всего такого с помощью фишек для скрэббла (ответ на него равен \(42\), на его вычисление ушло семь с половиной миллионов лет). Вопрос формулируется так: «Что получится в результате умножения 6 на 9?». Однако, этот вопрос не совсем удовлетворил ученых и они решили сконструировать компьютер, который умеет отвечать на «вспомогательные» вопросы жизни, вселенной и всего такого.

Такой компьютер был построен, но, к несчастью (но не неожиданно), результат вычислений был поврежден и частично утерян. Наконец, создателям компьютера удалось извлечь строку, которая является частью корректного вопроса. Внимательно проанализировав строку, ученые пришли к выводу, что вопрос может быть восстановлен из строки путем добавления некоторых букв к строке, при этом исходные буквы строки не могут быть переставлены или удалены. Также они уверены, что корректный вопрос представляет собой арифметическое выражение (как и главный вопрос), но, поскольку вопрос вспомогательный, то он не может содержать умножения — только сложение. Точнее, вопрос должен удовлетворять следующей грамматике:

::= | '+'

::= | '(' ')'

::= '0'...'9' []

Вам необходимо восстановить вопрос, основываясь на его части.

Входные данные

Единственная строка входного файла содержит поврежденный вопрос. Это непустая строка, состоящая не более чем из \(1000\) символов. Строка содержит только символы '+', '(', ')' а также цифры от 0 до 9.

Выходные данные

Выведите вопрос. Гарантируется, что существует корректный вопрос, длина которого не превышает \(5000\) символов, и вывод вашей программы также не должен превышать \(5000\) символов. Если вариантов восстановления вопроса несколько — выведите любой из них.

#1693
Бюрократия
  

Некогда гордая и свободолюбивая республика Акадия совсем погрязла в коррупции. Депутаты покупают и перепродают голоса друг друга, чтобы затем принять или отклонить какие-то законы. К принятым законам довольно быстро появляются поправки, их аннулирующие. Эти поправки, в свою очередь, аннулируются следующими поправками, и так далее. Секретарь премьер-министра хочет разобраться, какие законы в данный момент действуют, а какие нет.

С незапамятных времён в Акадии всего два типа законов:

* прямой закон, устанавливающий новые правовые нормы;
* поправка, аннулирующая какой-то из предыдущих законов.
Закон считается действующим тогда и только тогда, когда нет действующего закона, который бы являлся поправкой, его аннулирующей.

В распоряжении секретаря — все законы Акадии с момента становления республики в порядке их принятия. Помогите ему выяснить, какие из законов — действующие.

Входные данные

В первой строке ввода записано \(n\) (1 \(\le\) \(n\) \(\le\) 100000) — количество принятых законов.

Следующие \(n\) строк описывают сами законы. Каждое описание имеет следующий вид:

* «declare», если данный закон — это прямой закон.
* «cancel i», если данный закон — это поправка, аннулирующая закон с номером \(i\).

Законы нумеруются, начиная с единицы.

Выходные данные

В первой строке вывода выведите одно число — количество действующих законов. Далее выведите номера всех действующих законов в порядке возрастания.

Примеры
Входные данные
5
declare
cancel 1
declare
cancel 2
cancel 3
Выходные данные
3
1 4 5
#1697
Четыре камня
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
256 megabytes

Михаил — маг 80-го уровня. Одно из его изобретений — лабиринт, который дает сверхспособности каждому, кто проходит через него. Лабиринт имеет очень сложную магическую структуру, но внешне выглядит как квадрат, нарисованный на земле.

Михаил нашел подходящее место для лабиринта на берегу Клязьмы. Он нарисовал границу лабиринта палочкой на песке и отметил 4 точки на границах лабиринта так, что на каждой из сторон лабиринта лежал камень и ни один камень не лежал в углу.

В нашем мире все течет и меняется: река Клязьма по весне разлила свои воды, затопив пляж. Изображение на песке стерлось, остались только лежащие камни. Теперь Михаил не может восстановить свой лабиринт.

За помощь в восстановлении лабиринта Михаил обещал научить вас вставлять палочку в одно ухо и вынимать из другого.

Входные данные

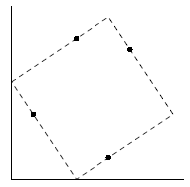
В четырех строках входного файла содержатся координаты камней \(x_i\) и \(y_i\) (-1000 ≤ \(x_i\), \(y_i\) ≤ 1000). Точки не совпадают и никакие три точки не лежат на одной прямой.

Выходные данные

Выведите четыре строки, каждая из которых содержит два вещественных числа — координаты вершин квадрата. Вершины должны быть перечислены в порядке обхода по или против часовой стрелки. Числа необходимо выводить с точностью 6 знаков после точки. Если решений несколько — выведите любое из них. Если решений нет — выведите 4 пары нулей

Примеры
Входные данные
6 13
11 12
9 2
2 6
Выходные данные
9.0 15.0
15.0 6.0
6.0 0.0
0.0 9.0
Входные данные
0 0
5 5
5 0
3 2
Выходные данные
0 0
0 0
0 0
0 0
#1699
Распознавание изображений
  

Новый проект Екатерины посвящен распознаванию изображений. При этом она решила применить инновационный подход, основанный на нанотехнологиях. Начать Екатерина решила с простого. Она выбрала d изображений, которые называются «цифрами» от \(0\) до \(d-1\). Каждое изображение представляет собой прямоугольник \(w\) на \(h\), заполненный белыми и черными квадратиками (назовем их пикселами). Все картинки различны (т.е. отличаются хотя бы одним пикселом).

Наноробот размещается в левом верхнем углу изображения и начинает выполнять программу, записанную на специальном языке программирования, описание которого приведено ниже. Задача робота состоит в том, чтобы понять, на какую из d картинок он помещен.

Язык программирования для наноробота содержит следующие команды:

'U', 'D', 'L', 'R' – команды перемещения вверх, вниз, влево и вправо соответственно. Если робот выходит за пределы изображения — программа считается ошибочной.

'(' ':' ')' - условный оператор. Робот смотрит на цвет пиксела, на котором он стоит. Если пиксел белый, то выполняется subprogram_w, если черный — subprogram_b.

'0', '1', …, '9' – команда распознавания. Робот должен выполнить одну из этих команд, когда он узнает, на каком изображении он расположен. После этой команды выполнение программы завершается.

Каждое перемещение занимает одну наносекунду. Выполнение условного оператора или оператора распознавания происходит мгновенно.

Ирина заинтересована в правильных программах. Т.е. если робот помещается на картинку, соответствующую цифре \(i\), то программа должна завершиться вызовом команды 'i'.

По данному описанию набора цифр составьте программу, время выполнения которой в худшем случае минимально.

Входные данные

Первая строка содержит три целых числа \(d, h\) и \(w (1 ≤ d, h, w ≤ 10)\) – количество изображений, высота и ширина изображений соответственно.

В следующих строках содержатся d описаний изображений. Каждое описание состоит из \(h\) строк по \(w\) символов в каждой. Символы могут быть двух типов: 'B' и 'W' и обозначать черный и белый пиксел соответственно.

Изображения даются в порядке от \(0\) до \(d-1\). Описания изображений разделены пустой строкой.

Выходные данные

Выведите корректную программу для наноробота, работающую за минимальное время в худшем случае. Если таких программ несколько — выведите любую из них. Пробелы при проверке будут игнорироваться.

Примеры
Входные данные
3 5 4
WBBW
BWWB
BWWB
BWWB
WBBW

WWBW
WBBW
BWBW
WWBW
WWBW

WBBW
BWWB
WWBW
WBWW
BBBB
Выходные данные
D(1:D(2:0))
Страница: << 226 227 228 229 230 231 232 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест