Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 283 284 285 286 287 288 289 >> Отображать по:
#2913
Рамки
  
Техническая задача. Сложность чуть выше средней.

Вася с Петей играют в интересную игру. Правила ее очень простые: есть две рамки и участники должны передвинуть вторую рамку так, что площадь пересечения рамок была бы как можно большой. Оба игрока думают в течение минуты и записывают вектор переноса второй рамки. Побеждает тот игрок, чей вектор переноса дал большую площадь пересечения.

Игра имеет много частных случаев, так что Вася решил сжульничать и написать программу, находящую лучший вектор переноса.

В этой игре рамкой называется фигура, состоящая из двух прямоугольников: внешнего и внутреннего. Внутренний прямоугольник лежит строго внутри внешнего. Стороны обоих прямоугольников параллельны координатным осям.

На первом рисунке указаны (1) неправильные рамки, (2) правильные рамки, (3) пересечение рамок.

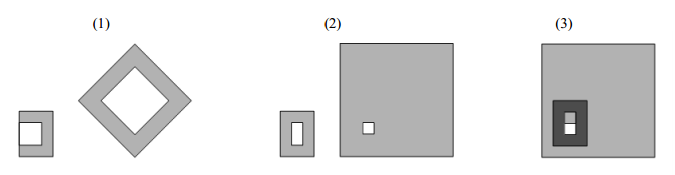
Площадь рамки вычисляется как W∙H – w∙h, где W, H – размеры внешнего прямоугольника, а w, h - размеры внутреннего (0 < w < W; 0 < h < H).

Напишите программу, которая находит перенос одной рамки относительно другой, которая даст максимальную площадь пересечения.

Входные данные

Каждая рамка описывается с помощью четырех точек — двух противоположных углов внешнего прямоугольника и двух противоположных углов внутреннего прямоугольника. Точки описываются своими координатами x и y, которые являются целыми числами и не превосходят 108 по модулю.

В первой строке содержится описание первой рамки, во второй — второй.

Выходные данные

Первая строка выходного файла должна содержать целое число A – максимальная площадь области пересечения данных рамок достижимая с помощью переноса.

Вторая строка должна содержать пару целых чисел x и y – координаты вектора переноса второй рамки который даст область пересечения A. Координаты не должны превосходить 1018 по абсолютному значению.

Примеры
Входные данные
2 2 5 6 3 3 4 5
0 0 10 10 2 2 3 3
Выходные данные
10
0 -4
#2914
Сусанин
  
Сложность выше среднего

Польская армия движется из Костромы в деревню Домнино. Два гетмана Стефан и Константин руководят армией. Стефан изучил карту дорог Костромской губернии и каждую ночь он ведет армию от одной деревни к некоторой другой по некоторой дороге. Константин достал карту секретных троп между деревнями и каждый день он возглавляет марш-бросок армии вдоль одной из этих троп. Каждый гетман перед маршем спрашивает дорогу у Ивана Сусанина. Таким образом, в первый день Стефан возглавляет поход, на следующий день - Константин, потом - снова Стефан и т.д.

Длина каждой дороги указана на карте Стефана. Поэтому Стефан знает минимальное расстояние от каждой деревни до Домнино, аналогично Константин знает минимальное расстояние до Домнино по своей карте. Иван Сусанин каждый раз выбирает дорогу для Стефана или тропу для Константина так, что минимальное расстояние между войском и Домнино по соответствующей карте все время строго убывает.

Помогите Ивану найти самый длинный путь в Домнино, удовлетворяющий этим условиям. Гарантируется, что Домнино достижимо из каждой деревни.

Входные данные

Первая строка входа содержит три целых числа N, S и T – количество деревень, номер начальной деревни и номер деревни Домнино (2 ≤ N ≤ 1000, 1 ≤ s, t ≤ N). Начальная точка не совпадает с Домнино.

Далее идут описание карты Стефана и карты Константина

Первая строка описания карты содержит число M – количество дорог или троп соответственно (1 ≤ M ≤ 100000). Каждая из следующих М строк содержит 3 целых числа a, b и l – описывающих дорогу/тропу между пунктами a и b с указанием длины l (1 ≤ a, b ≤ N; 1 ≤ l ≤ 106).

Выходные данные

Выведите общую длину пути (вдоль дорог и троп), который Сусанин заставит пройти польскую армию. Если он может заставить армию ходить вечно, так и не достигая Домнино, то выведите -1.

Примеры
Входные данные
5 1 5
5
1 2 2
1 4 2
2 3 1
3 4 1
5 3 1
4
1 2 2
2 4 2
2 3 1
2 5 2
Выходные данные
-1
Входные данные
3 1 3
4
1 2 10
2 3 10
1 3 20
2 3 30
4
2 1 10
1 3 10
1 1 10
2 3 10
Выходные данные
20
#2915
Кухня
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
256 megabytes

Роботы начинают все чаще использоваться в домашнем хозяйстве. Один программист решил сделать робота для своих хозяйственных нужд. Как известно, многие программисты потребляют напиток "Живчик", от которого на столе остаются разбросанные пустые бутылки. Поэтому он решил запрограммировать робота собирать пустые бутылки со стола.

Стол имеет форму прямоугольника длиной l и шириной w. Робот стартует в точке xr, yr, а N бутылок расположены в точках xi, yi (для i от 1 до N).

Чтобы убрать бутылку робот должен дойти до нее, взять ее, донести до любого края стола и сбросить. Робот может держать только одну бутылку, поэтому убирает он их по очереди.

Размером робота и бутылок можно пренебречь, в том числе можно считать что робот свободно может пройти мимо любой бутылки. Напишите программу, которая определяет минимальную длину пути робота, который ему необходимо пройти, чтобы убрать все бутылки со стола.

Входные данные

Первая строка входного файла содержит два целых числа w и l. (2 ≤ w, l ≤ 1000). Вторая строка входных данных содержит N – число бутылок на столе (1 ≤ N ≤ 18). Каждая из следующих N строк содержит два целых числа xi, yi – координаты i-й бутылки на столе (0<xi<w; 0<yi<l). Никакие две бутылки не находятся в одной точке.

Последняя строка входного файла содержит 2 целых числа xr, yr – координаты начальной позиции робота (опять же не у края стола и не в точке с бутылкой).

Выходные данные

Выведите длину кратчайшего пути робота с точностью не менее 6 значащих цифр после точки.

Примеры
Входные данные
3 4
2
1 1
2 3
2 1
Выходные данные
5.60555127546399
#2916
Дровосек
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Ответ считается как функции Гранди поддеревьев (\(X_i + 1\))

Двое играют в следующую игру: имеется дерево с отмеченной вершиной (корнем). За ход игрок разрубает ветку (стирает ребро), причем из двух получившихся компонент связности остается только та, которая содержит корень, другая удаляется. Проигрывает тот, кто не может сделать ход. Определите, может ли выиграть первый игрок, и если да, то укажите любой из его выигрышных ходов.

Входные данные

В первой строке вводится 2 числа — количество вершин 1 < N ≤ 100000 и номер корня 1 ≤ R ≤ N. В следующих N – 1 строках идут пары чисел — описания ребер.

Выходные данные

В первой строке выведите число 1 или 2 – номер победителя при правильной игре.

Если побеждает первый игрок, то во второй строке выведите порядковый номер ребра во входных данных, которое ему достаточно разрубить первым ходом (число от 1 до N – 1).

Примеры
Входные данные
2 1
1 2
Выходные данные
1
1
Входные данные
5 2
1 3
3 4
2 3
2 5
Выходные данные
2
#2917
Киоски с мороженым
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В маленьком провинциальном городке есть маленькая школа, в которой учатся не совсем большие дети. После занятий они бегут на автобусную остановку, откуда автобус развозит их по домам.

По дороге от школы до остановки есть N перекрестков, соединенных улицами. Школьники с улицы на улицу переходят только на перекрестках.

Все школьники, как известно, любят мороженое. Известная компания Cold-N-Icy, производящая мороженое, решила воспользоваться этим. Она хочет разместить киоски с мороженым на некоторых перекрестках таким образом, чтобы любой путь школьника от школы до остановки проходил хотя бы через один перекресток, на котором установлен киоск.

Так как установка и содержание киоска — дорогое дело, то компания решила привлечь Вас для того, чтобы определить минимальное число киосков, которое необходимо установить.

Помогите компании Cold-N-Icy найти это минимальное число.

Входные данные

В первой строке входного файла находится число перекрестков N (1 ≤ N ≤ 100).

В каждой из последующих N строк находится информация о перекрестках, соединенных улицами между собой. Перекрестки нумеруются, начиная с единицы. В начале i-той строки находится число Ki – количество мест (перекрестков, школы или остановки), соединенных улицами с i-тым перекрестком. Далее идет Ki мест, разделенных пробелами. Для обозначения перекрестков используются их номера, школа обозначается как school, остановка обозначается как station.

Если перекресток i находится в списке перекрестка j, то обратное также верно.

Гарантируется, что от школы до остановки всегда существует путь.

Выходные данные

Выведите одно число — минимальное число киосков, которые планируется установить.

Примеры
Входные данные
2
2 school station
2 station school
Выходные данные
2
Страница: << 283 284 285 286 287 288 289 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест