Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 290 291 292 293 294 295 296 >> Отображать по:
#2961
Упорядочить три числа
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Даны три числа, записанные в отдельных строках. Упорядочите их в порядке неубывания. 

Программа должна считывать три числа a, b, c, затем программа должна менять их значения так, чтобы стали выполнены условия a <= b <= c, затем программа выводит тройку a, b, c.

Входные данные

Вводятся три числа, каждое записано в отдельной строке.

Выходные данные

Выведите ответ на задачу.

Примеры
Входные данные
1
2
1
Выходные данные
1 1 2
#2962
Ход конем - 2
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить только так, как показано на рисунке:

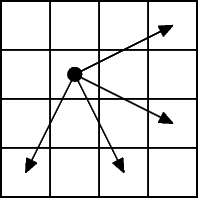
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.

Входные данные

В первой строке входного файла находятся два натуральных числа N и M (1 ≤ N, M ≤ 15).  

Выходные данные

В выходной файл выведите единственное число количество способов добраться конём до правого нижнего угла доски.

Примеры
Входные данные
4 4
Выходные данные
2
Входные данные
7 15
Выходные данные
13309
#2963
Калькулятор
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

Имеется калькулятор, который выполняет три операции:

  1. Прибавить к числу X единицу.
  2.  Умножить число X на 2.
  3. Умножить число X на 3.

Определите, какое наименьшее число операций необходимо для того, чтобы получить из числа 1 заданное число N.

Входные данные

Программа получает на вход одно число, не превосходящее 106.

Выходные данные

Требуется вывести одно число: наименьшее количество искомых операций.

Примеры
Входные данные
1
Выходные данные
0
Входные данные
5
Выходные данные
3
Входные данные
32718
Выходные данные
17
#2964
Попытка к бегству
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

Узник пытается бежать из замка, который состоит из N×M квадратных комнат, расположенных в виде прямоугольника NxM. Между любыми двумя соседними комнатами есть дверь, однако некоторые комнаты закрыты и попасть в них нельзя. В начале узник находится в левой верхней комнате и для спасения ему надо попасть в противоположную правую нижнюю комнату. Времени у него немного, всего он может побывать не более, чем в N+M-1 комнате на своем пути, то есть перемещаться он должен только вправо или вниз. Определите количество маршрутов, которые ведут к выходу.

Входные данные

Первая строчка входных данных содержит натуральные числа N и M, не превосходящих 1000. Далее идет план замка в виде N строчек из M чисел в каждой. Одно число соответствует одной комнате: 1 означает, что в комнату можно попасть, 0 – что комната закрыта.

Выходные данные

Программа должна напечатать количество маршрутов, ведущих узника к выходу и проходящих через M+N-1 комнату, или слово Impossible, если таких маршрутов не существует.

Входные данные подобраны таким образом, что искомое число маршрутов не превосходит 2.000.000.000.

Примеры
Входные данные
3 5
1 1 1 1 1
1 0 1 0 1
1 1 1 1 1
Выходные данные
3
#2965
Максимальная стоимость маршрута
  

В левом верхнем углу прямоугольной таблицы размером N×M находится черепашка. В каждой клетке таблицы записано некоторое число. Черепашка может перемещаться вправо или вниз, при этом маршрут черепашки заканчивается в правом нижнем углу таблицы.

Подсчитаем сумму чисел, записанных в клетках, через которую проползла черепашка (включая начальную и конечную клетку). Найдите наибольшее возможное значение этой суммы.

Формат входных данных

В первой строке входных данных записаны два натуральных числа N и M, не превосходящих 100 — размеры таблицы. Далее идет N строк, каждая из которых содержит M чисел, разделенных пробелами — описание таблицы. Все числа в клетках таблицы целые и могут принимать значения от 0 до 100.

Формат выходных данных

Программа должна вывести единственное число: максимальную возможную стоимость маршрута черепашки.
Ввод Вывод 
3 4
1 1 2 1
2 2 1 1
2 1 2 1
 
9

Страница: << 290 291 292 293 294 295 296 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест