Развлекательный телеканал транслирует шоу «Колесо Фортуны». В процессе игры участники шоу крутят большое колесо, разделенное на сектора. В каждом секторе этого колеса записано число. После того как колесо останавливается, специальная стрелка указывает на один из секторов. Число в этом секторе определяет выигрыш игрока.

Юный участник шоу заметил, что колесо в процессе вращения замедляется из-за того, что стрелка задевает за выступы на колесе, находящиеся между секторами. Если колесо вращается с угловой скоростью \(v\) градусов в секунду, и стрелка, переходя из сектора \(X\) к следующему сектору, задевает за очередной выступ, то текущая угловая скорость движения колеса уменьшается на \(k\) градусов в секунду. При этом если \(v \le k\), то колесо не может преодолеть препятствие и останавливается. Стрелка в этом случае будет указывать на сектор \(X\).

Юный участник шоу собирается вращать колесо. Зная порядок секторов на колесе, он хочет заставить колесо вращаться с такой начальной скоростью, чтобы после остановки колеса стрелка указала на как можно большее число. Колесо можно вращать в любом направлении и придавать ему начальную угловую скорость от \(a\) до \(b\) градусов в секунду.

Требуется написать программу, которая по заданному расположению чисел в секторах, минимальной и максимальной начальной угловой скорости вращения колеса и величине замедления колеса при переходе через границу секторов вычисляет максимальный выигрыш.

Многие системы форматирования текста, например TEX или Wiki, используют для разбиения текста на абзацы пустые строки. Текст представляет собой последовательность слов, разделенных пробелами, символами перевода строк и следующими знаками препинания: «,», «.», «?», «!», «-», «:» и «’» (ASCII коды 44, 46, 63, 33, 45, 58, 39). Каждое слово в тексте состоит из заглавных и прописных букв латинского алфавита и цифр. Текст может состоять из нескольких абзацев. В этом случае соседние абзацы разделяются одной или несколькими пустыми строками. Перед первым абзацем и после последнего абзаца также могут идти одна или несколько пустых строк.

Дальнейшее использование исходного текста предполагает его форматирование, которое осуществляется следующим образом. Каждый абзац должен быть разбит на строки, каждая из которых имеет длину не больше \(w\). Первая строка каждого абзаца должна начинаться с отступа, состоящего из \(b\) пробелов. Слова внутри одной строки должны быть разделены ровно одним пробелом. Если после слова идет один или несколько знаков препинания, они должны следовать сразу после слова без дополнительных пробелов. Если очередное слово вместе со следующими за ним знаками препинания помещается на текущую строку, оно размещается на текущей строке. В противном случае, с этого слова начинается новая строка. В отформатированном тексте абзацы не должны разделяться пустыми строками. В конце строк не должно быть пробелов.

Требуется написать программу, которая по заданным числам \(w\) и \(b\) и заданному тексту выводит текст, отформатированный описанным выше образом.

Отделу космических исследований поступило задание сфотографировать из космоса \(n\) объектов в заданной области. Область имеет форму квадрата размером \(50\times 50\) километров. Если разделить ее на квадраты размером \(1\times 1\) километр, то интересующие отдел объекты окажутся в центрах некоторых единичных квадратов.

Введем систему координат, направив ось OX с запада на восток и ось OY с юга на север. Тогда каждому единичному квадрату будут сопоставлены координаты в диапазоне от 1 до 50, как показано на рисунке ниже.

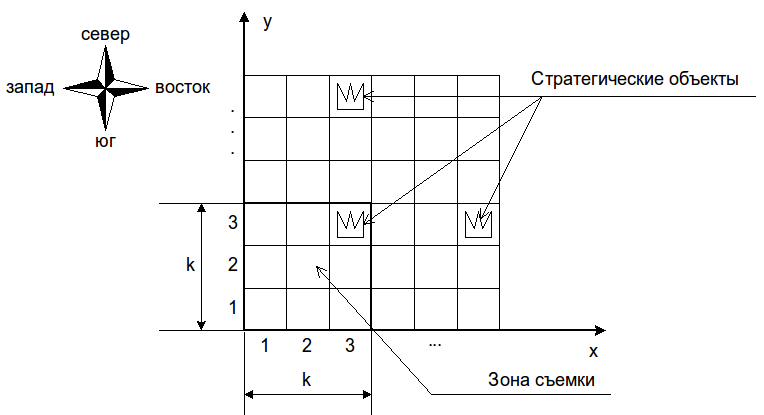
Для космической съемки используется специальный фотоаппарат высокого разрешения, установленный на космическом спутнике. Фотоаппарат может делать снимки квадратных участков земной поверхности размером \(k\times k\) километров. Исходно аппарат наведен на юго-западный угол заданной области, то есть, если сделать снимок, на нем будут видны единичные квадраты с координатами \(x\) и \(y\) от \(1\) до \(k\) километров.

С помощью специальных двигателей можно изменять орбиту спутника, что приводит к изменению участка съемки. За один день орбиту спутника можно изменить таким образом, что участок съемки сместится либо на один километр на запад, либо на один километр на восток, либо на один километр на север. Переместить участок съемки на юг невозможно. Непосредственно между перемещениями спутника можно сделать снимок, временем съемки можно пренебречь.

Руководство отдела заинтересовалось вопросом: за какое минимальное количество дней можно сделать снимки всех объектов заданной области.

Требуется написать программу, которая по заданному расположению объектов и размеру снимка \(k\) определит минимальное время, за которое можно сделать снимки всех объектов заданной области.