#3294

Параллелограмм (6-9)

Темы: [Элементарная геометрия]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 6-9 классы, 2011, Задача C ]

На уроке геометрии семиклассники Вася и Петя узнали, что такое параллелограмм. На перемене после урока они стали играть в игру: Петя называл координаты четырех точек в произвольном порядке, а Вася должен был ответить, являются ли эти точки вершинами параллелограмма.

Вася, если честно, не очень понял тему про параллелограммы, и ему требуется программа, умеющая правильно отвечать на Петины вопросы.

Напомним, что параллелограммом называется четырехугольник, противоположные стороны которого равны и параллельны.

Входные данные

В первой строке входного файла записано целое число \(N\) (\(1 \leq N \leq 10\)) - количество заданных Петей вопросов. Каждая из \(N\) последующих строк содержит описание четырех точек - четыре пары целых чисел \(X\) и \(Y\) (\(-100 \leq X\leq 100\), \(-100\leq Y \leq 100\)), обозначающих координаты точки. Гарантируется, что четыре точки, о которых идет речь в одном вопросе, не лежат на одной прямой.

Выходные данные

Для каждого из вопросов выведите "YES", если четыре заданные точки могут образовать параллелограмм, и "NO" в противном случае. Ответ на каждый из запросов должен быть в отдельной строке без кавычек.

Примеры

Входные данные

3
1 1 4 2 3 0 2 3
1 1 5 2 2 3 3 0
0 0 5 1 6 3 1 2

Выходные данные

YES
NO
YES

#3296

Поход (6-9)

Темы: [Динамическое программирование: два параметра]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 6-9 классы, 2011, Задача D ]

Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.

Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.

Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.

Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.

Входные данные

Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит \(200\) символов.

Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.

Выходные данные

Выведите одно целое число - минимальное количество переправ.

Примечание

Рисунок к приведенному выше примеру.

Примеры

Входные данные

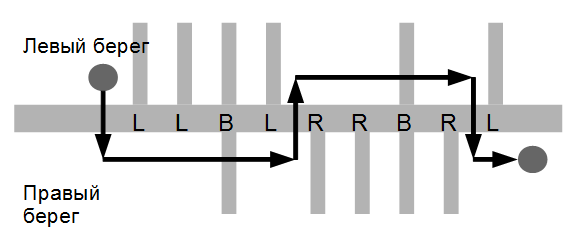
LLBLRRBRL

Выходные данные

#3297

Поход (10-11)

Темы: [Динамическое программирование: один параметр]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2011, Задача D ]

Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.

Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.

Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.

Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.

Входные данные

Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит \(10^5\) символов.

Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.

Выходные данные

Выведите одно целое число - минимальное количество переправ.

Примечания

Рисунок к приведенному выше примеру.

Примеры

Входные данные

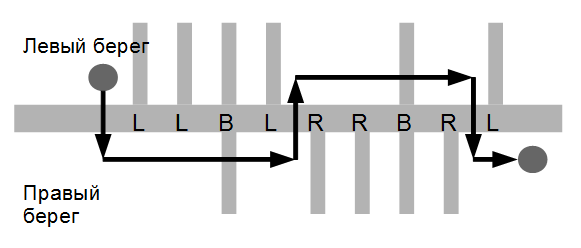
LLBLRRBRL

Выходные данные

#3299

Расширенный алгоритм Евклида

Темы: [НОД и алгоритм Евклида]

Даны натуральные числа a, b, c. Если уравнение ax+by=c имеет решения в целых числах, то выведите через пробел НОД(a,b), x и y (какое-нибудь решение). Если решения не существует, то выведите слово Impossible.

Входные данные

Входные данные - натуральные числа и не превышают по модулю 10000.

Выходные данные

Выведите ответ на задачу.

Примеры

Входные данные

1 2 3

Выходные данные

1 1 1

Входные данные

10 6 8

Выходные данные

2 2 -2

#3300

Простой максимальный поток

Темы: [Потоки] [Хеш]

Эта задача настолько проста, что у нее нет даже условия.

Дано N вершин неориентированного графа, M ребер, пропускная способность которых равна 1, и K запросов. Каждая вершина задается строкой, состоящей из маленьких латинских букв, длиной не более 10 символов. Для каждого запроса найдите величину максимального потока из одной вершины в другую. Вот и все.

Входные данные

В первой строке входного файла вводится 3 целых числа: N (1<=N<=5*10^5), M (0<=M<=5*10^5) и K (0<=K<=1000). Далее следует M строк, в каждой из которых через пробел записаны имена 2-ух вершин, что означает, что из одной вершины в другую есть ребро. Далее следует K запросов в том же виде, в котором задаются ребра. Запрос означает, что нужно вывести величину максимального потока из одной вершины в другую. Ответ на каждый запрос нужно выводить в отдельной строке. Гарантируется, что на вход поступает не более 2 запросов, при которых величина максимального потока положительна.

Выходные данные

Выведите ответ на поставленную задачу в указанном в условии формате.

Примеры

Входные данные

7 11 1
smity grepik
dop grepik
smity rojer
rojer dop
dop jack
sanek jack
dop sanek
hello sanek
hello grepik
dop hello
rojer jack
smity sanek

Выходные данные