Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Ася Вуткина - известный футбольный комментатор. Будучи профессионалом своего дела, Ася тщательно следит за всеми матчами всех европейских чемпионатов.
Благодаря накопленной информации, Ася может во время трансляции матча сообщить какую-нибудь интересную статистику, например: "Индзаги третий матч подряд забивает гол на 9-й минуте" или "Матерацци никогда не открывает счет в матче".
Но мозг Аси не безграничен, а помнить всю историю футбола просто невозможно. Поэтому Ася попросила вас написать программу, которая собирает статистику матчей и умеет отвечать на некоторые запросы, касающиеся истории футбола.
Информация о матче сообщается программе в следующей форме:
"Название 1-й команды" - "Название 2-й команды" Счет 1-й команды:Счет 2-й команды
Автор 1-го забитого мяча 1-й команды Минута, на которой был забит мяч'
Автор 2-го забитого мяча 1-й команды Минута, на которой был забит мяч'
...
Автор последнего забитого мяча 1-й команды Минута, на которой был забит мяч'
Автор 1-го забитого мяча 2-й команды Минута, на которой был забит мяч'
...
Автор последнего забитого мяча 2-й команды> <Минута, на которой был забит мяч>'
Запросы к программе бывают следующих видов:
Total goals for Название команды
- количество голов, забитое данной командой за все матчи.
Mean goals per game for Название команды
- среднее количество голов, забиваемое данной командой за один матч. Гарантирутся, что к моменту подачи такого запроса команда уже сыграла хотя бы один матч.
Total goals by Имя игрока
- количество голов, забитое данным игроком за все матчи.
Mean goals per game by Имя игрока
- среднее количество голов, забиваемое данным игроком за один матч его команды. Гарантирутся, что к моменту подачи такого запроса игрок уже забил хотя бы один гол.
Goals on minute Минута by Имя игрока
- количество голов, забитых данным игроком ровно на указанной минуте матча.
\texttt{Goals on first <\(T\)> minutes by <Имя игрока>}\\ --- количество голов, забитых данным игроком на минутах с первой по \(T\)-ю включительно.Goals on last \(T\) minutes by Имя игрока
- количество голов, забитых данным игроком на минутах с \((91 - T)\)-й по 90-ю включительно.
Score opens by Название команды
- сколько раз данная команда открывала счет в матче.
Score opens by Имя игрока
- сколько раз данный игрок открывал счет в матче.
Входной файл содержит информацию о матчах и запросы в том порядке, в котором они поступают в программу Аси Вуткиной.
Во входном файле содержится информация не более чем о 100 матчах, в каждом из которых забито не более 10 голов. Всего в чемпионате участвует не более 20 команд, в каждой команде не более 10 игроков забивают голы.
Все названия команд и имена игроков состоят только из прописных и строчных латинских букв и пробелов, а их длина не превышает 30. Прописные и строчные буквы считаются различными. Имена и названия не начинаются и не оканчиваются пробелами и не содержат двух пробелов подряд. Каждое имя и название содержит хотя бы одну букву.
Минута, на которой забит гол - целое число от 1 до 90 (про голы, забитые в дополнительное время, принято говорить, что они забиты на 90-й минуте).
Для простоты будем считать, что голов в собственные ворота в европейских чемпионатах не забивают, и на одной минуте матча может быть забито не более одного гола (в том числе на 90-й). Во время чемпионата игроки не переходят из одного клуба в другой.
Количество запросов во входном файле не превышает 500.
Для каждого запроса во входном файле выведите ответ на этот запрос в отдельной строке. Ответы на запросы, подразумевающие нецелочисленный ответ, должны быть верны с точностью до трех знаков после запятой.
"Juventus" - "Milan" 3:1 Inzaghi 45' Del Piero 67' Del Piero 90' Shevchenko 34' Total goals for "Juventus" Total goals by Pagliuca Mean goals per game by Inzaghi "Juventus" - "Lazio" 0:0 Mean goals per game by Inzaghi Mean goals per game by Shevchenko Score opens by Inzaghi
3 0 1.0 0.5 1.0 0
Total goals by Arshavin
0
Коля учится в третьем классе, сейчас они проходят простые дроби с натуральными числителем и знаменателем. Вчера на уроке Коля узнал, что дробь называется правильной, если ее числитель меньше знаменателя, и несократимой, если нет равной ей дроби с меньшими натуральными числителем и знаменателем.
Коля очень любит математику, поэтому дома он долго экспериментировал, придумывая и решая разные задачки с правильными несократимыми дробями. Одну из этих задач Коля предлагает решить вам с помощью компьютера.
Найдите наибольшую правильную несократимую дробь, у которой сумма числителя и знаменателя равна \(n\).
Во входном файле записано одно целое число \(n\) (\(3\le n\le 1000\)).
Выведите в выходной файл числитель и знаменатель искомой дроби.
10
3 7
23
11 12
В 314 уровне компьютерной игры "Болото 2" лягушонку Квайту предстоит решить непростую задачу. На прямой расположены \(n\) листьев водяной лилии, на каждом из которых сидит большая муха. Находясь на одном из листьев, он может прыгнуть на соседний лист или перепрыгнуть через один лист в любую сторону и съесть сидящую там муху.
Квайт уже большой лягушонок, а листья не очень надежные, поэтому когда он прыгает на какой-то лист и съедает сидящую на нем муху, лист начинает тонуть, так что Квайт должен сразу же прыгать дальше.

Для того, чтобы продолжать приключения, Квайту необходимо съесть всех мух, начав свой путь с листа номер \(a\) и закончив на листе номер \(b\) (листья пронумерованы вдоль прямой последовательными натуральными числами, начиная с единицы).
Помогите Квайту пройти этот уровень.
Во входном файле записаны три целых числа, разделенных пробелами \(n\), \(a\) и \(b\) (\(2\le n\le 1000\), \(1\le a, b\le n\), \(a \ne b\)).
В выходной файл выведите \(n - 1\) число - последовательность прыжков, которые нужно сделать Квайту. Прыжок задается числом \(-2\), \(-1\), \(1\) или \(2\), это число означает разность между номером листа, на котором оказывается Квайт, и номером листа, на котором он находится перед прыжком.
Если не существует пути, удовлетворяющего требованиям, выведите одно число 0.
5 2 4
-1 2 2 -1
4 2 3
0
Игорь работает младшим лаборантом в НИИ ихтиологии. Ему вверены \(n\) аквариумов, стоящих в ряд, в каждом из которых живет колония рыбок гуппи. Про каждую колонию заранее известна ее численность.
В лабораторных условиях НИИ ихтиологии колония рыбок гуппи растет по следующему правилу: достигнув популяции в \(f\) рыбок, колония живет в течении \(max(1000 - f, 1)\) секунд, после чего на свет появляется новая рыбка. От начального момента времени до рождения первой рыбки колония размера \(f\) также ждет \(max(1000 - f, 1)\) секунд.
Например, колония с начальным размером 996 будет размножаться следующим образом:
| момент времени | размер колонии | время до очередной рыбки |
|---|---|---|
| 0 | 996 | 4 |
| 4 | 997 | 3 |
| 7 | 998 | 2 |
| 9 | 999 | 1 |
| 10 | 1000 | 1 |
| 11 | 1001 | 1 |
| 12 | 1002 | 1 |
| ... | ... | ... |
Появление на свет каждой новой рыбки Игорь должен фиксировать в специальном журнале. Будем считать, что запись он делает мгновенно, но при этом он должен в момент рождения новой рыбки находиться рядом с аквариумом, в котором это произошло.
На перемещение от одного аквариума к соседнему у Игоря уходит одна секунда. В начальный момент времени Игорь стоит около первого аквариума.
Вычислите, в течение какого наибольшего периода времени Игорь сможет добросовестно выполнять свою работу.
В первой строке входного файла содержится целое число \(n\) (\(2 \le n \le 50\)) - количество аквариумов с рыбками гуппи в НИИ ихтиологии. Каждая из следующих \(n\) строк содержит одно целое число \(a_i\) (\(1 \le a_i \le 2007\)) - численность \(i\)-й колонии.
В выходной файл выведите момент времени, когда родится первая рыбка гуппи, запись о рождении которой Игорь сделать не сможет.
В приведенном примере Игорь сначала ждет у первого аквариума появления рыбки на 4-й секунде. После этого он бежит к третьему аквариуму (на это у него уходит 2 секунды) и как раз успевает к рождению рыбки на 6-й секунде. Однако вернуться к первому аквариуму, где следующая рыбка родится на 7-й секунде, он уже не успевает.
3 996 1 994
7
Антон - большой любитель компьютерных игр. Совсем недавно вышла новая игра Heroes of Keyboard and Mouse, и он, конечно же, сразу ее купил и установил на свой компьютер. Эта игра относится к жанру квестов, и поэтому ее прохождение сводится к последовательному выполнению ряда заданий (квестов).
Один из квестов, над которым Антон бьется уже не первый день состоит в том, что требуется открыть замок. Замок состоит из \(n\) шестеренок, стоящих в ряд - \(i\)-ая из шестеренок имеет \(s_i\) зубцов, на каждом из которых написано число от \(0\) до \(s_i - 1\). Первая шестеренка зацеплена только со второй, вторая зацеплена с первой и третьей, третья - со второй и четвертой, ..., \((n-1)\)-ая - с \((n-2)\)-ой и \(n\)-ой, \(n\)-ая только с \((n-1)\)-ой.
На замке имеется \(n\) окошечек и \(n\) ручек - в \(i\)-ое окошко можно видеть число, написанное на одном из зубцов \(i\)-ой шестеренки, а с помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. При этом числа на шестеренках расположены таким образом, что если до поворота \(i\)-ой из них по часовой стрелке на одно деление в \(i\)-ом окошке было видно число \(x\), то после поворота будет видно число \((x+1) \bmod s_i\). Аналогично, после поворота против часовой стрелки на одно деление вместо числа \(x\) будет видно число \((x-1+s_i) \bmod s_i\). Разумеется, если шестеренку повернуть по часовой стрелке, то непосредственно зацепленные с ней шестеренки повернутся против часовой стрелки, и наоборот, если шестеренку повернуть против часовой стрелки, то они повернутся по часовой стрелке. Слева на рис.1 показано положение шестеренок до поворота первой из них по часовой стрелке, справа на рис. 1 показано положение шестеренок после указанного поворота. Более толстыми линиями нарисован тот зубец шестеренки, число на котором видно в соответствующее окошко замка.
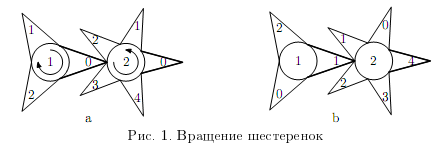
Изначально замок находится в состоянии, в котором в \(i\)-ое окошко видно число \(a_i\). Для того, чтобы его открыть, необходимо перевести его в состояние, в котором в \(i\)-ое окошко видно число \(b_i\).
С помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. Разумеется, если повернуть \(i\)-ую шестеренку, то придут в движение и все шестеренки, с которыми она соединена - напрямую или через другие шестеренки. Поворот любой шестеренки на одно деление занимает одну секунду. Кроме этого, если \(i\)-ая шестеренка находится в таком состоянии, что в \(i\)-ое окошко видно число \(b_i\) (то есть, она находится в положении, соответствующем требуемому состоянию замка), то ее можно вдавить, нажав на ее ручку. В результате этого \(i\)-ая шестеренка перестает быть соединенной с \((i-1)\)-ой и \((i+1)\)-ой (если, конечно, они существуют). Вдавленная шестеренка остается в таком состоянии навсегда. На то, чтобы нажать на ручку и вдавить шестеренку требуется \(k\) секунд. На рис. 2 слева показано положение шестеренок до вдавливания второй из них, а справа - после вдавливания и после поворота первой по часовой стрелке, а третьей - против. Отметим, что после вдавливания второй шестеренки первая и третья вращаются независимо друг от друга.
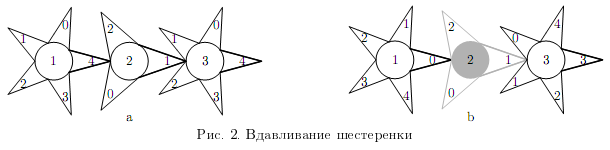
Для того, чтобы выполнить квест, Антону необходимо открыть замок как можно быстрее. Напишите программу, которая по описанию замка, его начального состояния и требуемого состояния, вычислит минимальное время, за которое Антон может открыть замок.
Первая строка входного файла содержит два целых числа: \(n\) и \(k\) (\(1 \le n \le 25\), \(1 \le k \le 100\)). Вторая строка входного файла содержит \(n\) чисел: \(s_1\), \(s_2\), ..., \(s_n\) - размеры шестеренок. Все \(s_i\) - целые числа от 3 до 10. Третья строка входного файла содержит \(n\) целых чисел \(a_1\), \(a_2\), ..., \(a_n\) - начальные положения шестеренок (для всех \(a_i\) выполняются неравенства \(0 \le a_i < s_i\)). Четвертая строка входного файла содержит \(n\) целых чисел \(b_1\), \(b_2\), ..., \(b_n\) - требуемые положения шестеренок (для всех \(b_i\) выполняются неравенства \(0 \le b_i < s_i\)).
В выходной файл выведите минимальное количество времени, которое необходимо для того, чтобы открыть замок.
2 2 3 5 0 0 1 1
4
3 2 3 3 3 0 0 0 1 1 1
5