Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 423 424 425 426 427 428 429 >> Отображать по:
#111409
Электричество
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Вы отвечаете за электрическую сеть для некоторого соревнования по программированию и вам надо подключить много компьютеров к источнику питания. К сожалению, есть два стандарта для вилок и розеток: A и B. Эти стандарты несовместимы между собой, так что вилка стандарта A может быть включена только в розетку стандарта А, и вилка стандарта B может быть включена только в розетку стандарта B.

В зале соревнований есть только одна розетка стандарта A. Каждый компьютер, который будет использован в соревновании, имеет вилку стандарта A. Таким образом, только один компьютер может быть подключен напрямую к главной розетке. Но вы можете использовать разветвители питания двух типов.

  • Разветвитель первого типа имеет одну вилку стандарта A и несколько розеток стандарта B.
  • Разветвитель второго типа имеет одну вилку стандарта B и несколько розеток стандарта A.

Все разветвители питания очень мощные и могут выдержать любую нагрузку. Так что вы можете создать электрическую сеть, подключив один разветвитель первого типа к главной розетке, затем несколько разветвителей второго типа к этому разветвителю, и так далее. В конце вы получите несколько розеток, к которым вы можете присоединить компьютеры.

Вы должны найти максимальное число компьютеров, которые могут быть подключены к сети, используя доступные разветвители.

Возможное решение для первого примера: 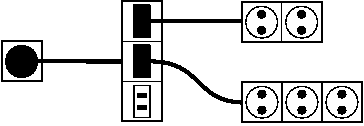Возможное решение для второго примера: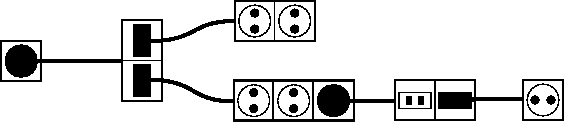

Входные данные

Первая строка входного файла содержит два целых числа n и m — количество разветвителей первого и второго типа (0 ≤ n, m ≤ 100 000).

Вторая строка содержит n целых чисел ai — количество розеток на i-том разветвителе первого типа (1 ≤ ai ≤ 1000).

Третья строка содержит m целых чисел bi — количество розеток на i-том разветвителе второго типа (1 ≤ bi ≤ 1000).

Выходные данные

Выведите максимальное количество компьютеров, которое может быть подключено к сети.

Примеры тестов

Входные данные
3 2
3 2 1
2 3
Выходные данные
5
Входные данные
2 3
2 2
2 3 1
Выходные данные
5

Решения, работающие в случае, если N и M не превосходят 100, будут набирать не менее 30 баллов.

#111410
Результаты гонки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Формула TheByte это самое известное гоночное соревнование в Байтландии. Соревнование уже завершено и каждый из n гонщиков заработал какое-то целое неотрицательное количество очков. Гонщик, у которого больше очков, займет более высокое место.

Окончательные результаты еще не объявлены, но уже известно, что сумма все зарабонных гонщиками очков равна p, и среди лучших k гонщиков есть только d различных результатов.

Байтланд Таймс просит вас угадать окончательные результаты, основываясь на данной информации.

Входные данные

Единственная строка входного файла содержит четыре целых числа: n — количество гонщиков, p — суммарное количество очков, k и d — количество различных результатов среди k лучших гонщиков (1 ≤ k ≤ n ≤ 1000; 0 ≤ p ≤ 1 000 000; 1 ≤ d ≤ k).

Выходные данные

Выведите возможные результаты, которые соответствуют данным n, p, k и d.

Если возможно создать корректные результаты, вы должны вывести n строк, i-тая из которых будет содержать количество очков, заработанных i-тым гонщиком. Гонщики должны быть упорядочены по убыванию количества очков.

Если не существует возможных результатов, удовлетворяющих данной информации, выведите одну строку "Wrong information".

Система оценки
  • Подзадача 0 (0 баллов) Тесты из условия.
  • Подзадача 1 (15 баллов) \( n \le 10, p \le 10\).
  • Подзадача 2 (21 баллов) \( n \le 10\). Необходимые подгруппы: 1.
  • Подзадача 3 (24 баллов) \( n \le 18\). Необходимые подгруппы: 1, 2.
  • Подзадача 4 (15 баллов) \( p \le 2000\). Необходимые подгруппы: нет.
  • Подзадача 5 (25 баллов) Без дополнительных ограничений. Необходимые подгруппы: 1, 2, 3, 4.

Примеры тестов

Входные данные
3 4 2 2
Выходные данные
2
1
1
Входные данные
3 5 2 2
Выходные данные
3
2
0
Входные данные
2 5 2 1
Выходные данные
Wrong information

#111411
Сетка
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Геральд потратил несколько часов, рисуя прямоугольную сетку на листе бумаги. Сначала он нарисовал несколько вертикальных линий на одинаковом расстоянии dx между ними. После этого он нарисовал несколько горизонтальных линий. Они также находились на одинаковом расстоянии dy друг от друга.

Пока Геральд отдыхал от трудов, его брат Майк пришел и нарисовал прямую линию на листе бумаги. Геральд разозлился и приказал Майку стереть все лишнее с бумаги.

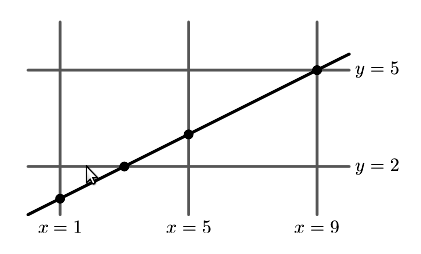
Но Майк не воспринял всерьез слова брата и стер все. Но он заметил, что точки пересечения его линии с сеткой были достаточно жирными для того, чтобы быть заметными даже после стирания.

Помогите Геральду восстановить параметры исходной сетки.

Входные данные

Первая строка входного файла содержит одно целое число n — количество точек пересечения (3 ≤ n ≤ 100 000).

Каждая из следующих n строк содержит два целых числа xi, yi — координаты одной из точек пересечения. Координаты не превосходят 109 по абсолютной величине.

Все точки пересечения различны. Других общих точек, кроме описанных выше, у сетки и прямой Майка нет.

Выходные данные

Выведите шесть целых чисел x1, x2, dx, y1, y2 и dy. Первые три числа описывают набор вертикальных прямых: минимальная x-координата вертикальной прямой, максимальная x-координата вертикальной прямой и расстояние между соседними вертикальными линиями ( - 109 ≤ x1 ≤ x2 ≤ 109; 0 < dx ≤ 2·109). Следующие три числа аналогично описывают набор горизонтальных линий ( - 109 ≤ y1 ≤ y2 ≤ 109; 0 < dy ≤ 2·109).

Гарантируется, что хотя бы одно решение существует.

Примеры тестов

Входные данные
4
1 1
5 3
3 2
9 5
Выходные данные
1 9 4 2 5 3

#111423
Поиск шаблона
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Шаблоном называется любая непустая строка, состоящая из маленьких латинских букв и символов "*".

Будем говорить, что строка T подходит под шаблон P, если в P можно символы "*" так заменить на последовательности букв латинского алфавита (возможно, пустые), что в итоге получится строка T. К примеру, строка aadbc походит под шаблон a*b*c, т.к. можно первую звездочку заменить на последовательность букв ad, а вторую — на пустую последовательность, в результате чего получится искомая строка.

Циклическом сдвигом строки называется строка, полученная перемещением нескольких букв из строки в ее начало. Для заданного шаблона P и строки T найдите, сколько циклических сдвигов строки T подходят под шаблон P.

Входные данные

Первая строка входных данных содержит шаблон P, длиной не более 100 символов. Вторая строка содержит исходную строку T, длиной не более 100 000 символов. Все строки имеют длину не менее одного символа.

Выходные данные

Выведите единственное число — искомое число циклических сдвигов, подходящих под шаблон.

Примеры тестов

Входные данные
aaaa
aaaa
Выходные данные
4
Входные данные
a*a
aaaaaa
Выходные данные
6
Входные данные
*a*b*c*
abacabadabacaba
Выходные данные
15

#111426
Раздел имущества
  
Темы: [meet in the middle]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В этой задаче входные данные записаны в файле exchange.in, вывод нужно записать в файл exchange.out.

Вася — профессиональный юрист, и сейчас он рассматривает очередное дело о разделе имущества. Всего имеется N наследников, каждый из них имеет значимость Ri. Богатый дедушка оставил им состояние в размере L иностранных тугриков. Логично раздать наследство пропорционально значимости, в этом случае i-ый наследник получит 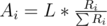иностранных тугриков. Однако, наследники очень привередливы, поэтому наследник желает получить кругленькую сумму, т.е. ту, которая делится на Si.

Чтобы выполнить просьбу наследников, Вася может округлять числа Ai до ближайшего, делящегося на Si (в случае, если делимость не имеет места). При этом, Вася сам выбирает, округлить очередное число вниз или вверх. Пусть Bi означает, сколько в итоге получит очередной наследник. Так как Вася — честный человек, он хочет минимизировать 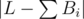. В случае нескольких вариантов, он выбирает тот, при котором 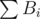будет наименьшей.

Входные данные

В первой строке входных данных содержится два целых числа N и L — количество наследников и размер состояния, соответственно (1 ≤ N ≤ 30, 1 ≤ L ≤ 109). В следующей строке содержатся значимости наследников Ri (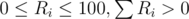). В следующей строк содержатся числа Si (1 ≤ Si ≤ 109).

Выходные данные

Выведите единственное число — искомую оптимальную сумму .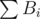

Примеры тестов

Входные данные
2 250
1 2
100 150
Выходные данные
250
Входные данные
3 1000
25 25 50
34 77 52
Выходные данные
989
Входные данные
3 10
1 1 0
50 50 50
Выходные данные
0

Страница: << 423 424 425 426 427 428 429 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест