Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
В последнее время в одной из школ Н. Новгорода, а также на одном из факультетов ННГУ стала очень популярна игра в настольный теннис. Игроки часто сталкиваются со следующей проблемой: довольно трудно уследить за всем ходом матча и при этом не сбиться со счёта, поэтому очень хотелось бы иметь программу, подсчитывающую счёт. Напишите программу, которая по данному протоколу матча восстановит итоговый счёт.
Протокол состоит из последовательности следующих событий: service, net, out, goal, return, eom.
События обозначают следующее:
* service — подача (при этом игрок ударяет по мячу). service — всегда первое событие во входном файле. После него могут следовать net, out, goal, return.
* net — мяч ударяется о половину поля того игрока, который ударял по мячу последним, слишком много раз. Игрок, который ударял по мячу последним, проигрывает розыгрыш. После этого события могут идти service или eom.
* out — мяч уходит в аут. Игрок, который ударял по мячу последним, проигрывает розыгрыш. После этого события могут идти service или eom.
* goal — игрок, который ударял по мячу последним, забивает гол (т.,е. выигрывает розыгрыш). Далее может быть service или eom.
* return — игрок отбивает мяч, ударяя по нему (игроки ударяют по мячу по очереди). Далее может быть net, out, goal, return.
* eom — матч окончен. Это всегда последнее событие.

Когда игрок выигрывает розыгрыш, ему начисляется очко. Когда игрок проигрывает розыгрыш, очко начисляется его противнику.
Подачи подаются по пять штук, т.,е. первые пять подач подаёт первый игрок, следующие пять — другой и т.д. Полное количество подач может быть не кратным пяти, в таком случае последняя серия подач будет короче пяти штук.
Конечно, в реальном матче может произойти ситуация, которую невозможно описать этими событиями, но ваша программа должна считать, что весь матч описывается данными во входном файле событиями.
Во входном файле находится список событий. События расположены по одному на строке без пробелов. Последовательность событий удовлетворяет всему, что было сказано выше; пустых строк во входном файле нет (кроме, возможно, строк после события eom). Всего событий не более 50000.
В выходной файл выведите два числа: очки того, кто подавал первым, потом — очки его противника.
service goal service out service net service return return return out service return goal service goal eom
2 4
service out eom
0 1
На плоскости заданы дуга окружности, отрезок и точка. Как отрезок, так и дуга окружности непрозрачны. Определите, какая часть дуги видна из этой точки.
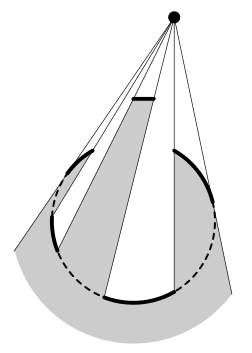
Входной файл состоит из трёх строк, описывающих данные объекты. Первая строка описывает дугу и содержит пять чисел — координаты центра дуги, радиус дуги, полярный угол точки начала дуги и полярный угол точки конца дуги. Полярные углы заданы в градусах
и отсчитываются относительно центра дуги против часовой стрелки от положительного направления оси \(x\). Вторая строка описывает точку и содержит два числа — её координаты. Третья строка описывает отрезок и содержит четыре числа — координаты
начала и конца отрезка. Все числа во входном файле вещественны и не превосходят \(10^6\) по модулю. Гарантируется, что как радиус окружности, так и длина отрезка больше нуля, что полярный угол конца дуги больше, чем полярный угол начала, и
что разность этих углов не превосходит 360.
Гарантируются, что никакие два из данных трёх объектов не имеют общих точек.
Выведите в выходной файл одно число на отрезке от 0 до 1 — относительную часть дуги, которая видна из данной точки. Ваш ответ должен отличаться от правильного не более, чем на 10−4.
2 1 2 120 420 3 6 2 4 2.5 4
0.496842552858631315
Фирма, в которой работает ваш друг, решила воспользоваться удобным моментом и купила компанию, занимающуюся пригородными автобусными пассажирскими перевозками. Таким образом, фирма вашего друга расширяет область деятельности и будет теперь обслуживать и некоторые внутриобластные автобусные маршруты.
Сейчас руководство фирмы, и в том числе ваш друг, заняты оптимизацией работы этих маршрутов. Одна из основных проблем, которые были обнаружены, состоит в том, что большинство автобусов, использующихся там, очень старые и изношенные, и поэтому часто выходят из строя. В целях улучшения ситуации было принято решение о создании сети ремонтных подстанций, которые будут располагаться в некоторых населённых пунктах области и обслуживать другие близлежащие населённые пункты.
Система дорог в области устроена следующим простым образом. Есть \(N\) населённых пунктов, некоторые из которых соединены дорогами. Между каждой парой пунктов существует не более одной дороги, и более того, для каждой пары населённых пунктов есть ровно один способ добраться из одного в другой (возможно, через промежуточные посёлки).
В каждом населённом пункте можно разместить ремонтную подстанцию. В принципе, фирма может размещать как крупные подстанции, которые даже в одиночку смогут обслуживать всю область, но при этом будут требовать больших расходов на содержание, так и небольшие станции, которые будут обслуживать лишь прилегающие населённые пункты, но при этом будут обходиться намного дешевле. Фирма уже определила, что каждую подстанцию можно характеризовать параметром “мощность”, которая может принимать значения, являющиеся целыми положительными числами (равна нулю мощность быть не может). Подстанция с мощностью \(k\) будет обслуживать населённый пункт u, в котором она расположена, и все другие населённые пункты, до которых можно добраться из u, использовав не более k дорог (т.е. при \(k\)=1, например, подстанция обслуживает свой населённый пункт и все, которые напрямую соединены с ним дорогой). Стоимость содержания такой подстанции пропорциональна её мощности.
Теперь перед руководством фирмы и, в частности, вашим другом, стоит задача придумать схему расположения подстанций в населённых пунктах области так, чтобы, во-первых, каждый населённый пункт обслуживался хотя бы одной подстанцией, а во-вторых, суммарная мощность созданных подстанций была минимальна.
Как показывает статистика, автобусы намного реже ломаются на дорогах, чем внутри населённых пунктов, где они вынуждены часто изменять скорость, останавливаться, трогаться с места, заводить двигатель и т.д., поэтому не важно, все ли дороги обслуживаются — главное, чтобы обслуживались все населённые пункты.
В первой строке входного файла находится одно число \(N\) — количество населённых пунктов в области (1<=\(N\)<=300). Далее следуют \(N\)−1 строка, описывающая дороги. Каждая строка содержит два числа — номера населённых пунктов, которые соединяет эта дорога. Населённые пункты нумеруются от 1 до \(N\).
В первую строку выходного файла выведите одно число — оптимальную суммарную мощность подстанций. Далее выведите \(N\) чисел, описывающих какое-нибудь оптимальное решение. \(i\)-ое из этих чисел должно быть равно мощности подстанции, которую в вашем решении надо расположить в пункте \(i\), или 0, если в населённом пункте \(i\) не должна находиться подстанция.
5 1 2 1 3 1 4 1 5
1 1 0 0 0 0
В Команде проходит традиционная ежегодная олимпиада по теории магии среди младшекурсников. Завхозу смены Кате Медведевой поручили заняться распределением студентов по аудиториям.
Каждый факультет выставил своих лучших учеников на олимпиаду. От Звездочек участвует G студентов, от Солнышек S студентов, Травинок представляет H студентов и Подсолнухов — R студентов. В распоряжении Медведевой находится M аудиторий. На аудитории наложено особое заклятие расширения, поэтому при необходимости они могут вместить любое количество студентов. При рассадке необходимо учесть, что ученики одного факультета, находящиеся в одной аудитории, могут, воспользовавшись случаем, начать жульничать, обмениваясь идеями по решению задач. Поэтому в любой аудитории количество студентов с одного факультета, попавших в нее, следует свести к минимуму. Назовем рассадку, удовлетворяющую такому требованию, оптимальной.
Помогите посчитать, какое минимальное количество студентов с одного факультета все же придется посадить в одной аудитории даже при оптимальной рассадке.
В первой строке идут четыре целых числа G, S, H и R (1 ≤ G, S, H, R ≤ 1000) — количество учеников, представляющих каждый из факультетов школы.
Во второй строке идет целое число M (1 ≤ M ≤ 1000) — количество классов в распоряжении у завхоза.
Выведите минимальное количество студентов с одного факультета, которое Кате придётся посадить в одну аудиторию даже при оптимальной рассадке.
4 3 4 4
2
2
15 14 13 14
5
3
Лёша сидел на лекции. Ему было невероятно скучно. Голос лектора казался таким далеким и незаметным...
Чтобы окончательно не уснуть, он взял листок и написал на нём свое любимое слово. Чуть ниже он повторил своё любимое слово, без первой буквы. Ещё ниже он снова написал своё любимое слово, но в этот раз без двух первых и последней буквы.
Тут ему пришла в голову мысль — времени до конца лекции все равно ещё очень много, почему бы не продолжить выписывать всеми возможными способами это слово без какой-то части с начала и какой-то части с конца?
После лекции Лёша рассказал Максу, как замечательно он скоротал время. Максу стало интересно посчитать, сколько букв каждого вида встречается у Лёши в листочке. Но к сожалению, сам листочек куда-то запропастился.
Макс хорошо знает любимое слово Лёши, а ещё у него не так много свободного времени, как у его друга, так что помогите ему быстро восстановить, сколько раз Лёше пришлось выписать каждую букву.
На вход подаётся строка, состоящая из строчных латинских букв — любимое слово Лёши.
Длина строки лежит в пределах от 5 до 100 000 символов.
Для каждой буквы на листочке Лёши, выведите её, а затем через двоеточие и пробел сколько раз она встретилась в выписанных Лёшей словах (см. формат вывода в примерах). Буквы должны следовать в алфавитном порядке. Буквы, не встречающиеся на листочке, выводить не нужно.
hello
e: 8
h: 5
l: 17
o: 5
abacaba
a: 44
b: 24
c: 16
Пояснение к первому примеру. Если любимое Лёшино слово — "hello", то на листочке у Лёши будут выписаны следующие слова: