Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 431 432 433 434 435 436 437 >> Отображать по:
#111572
Военный полигон
  
Ограничение по времени, сек0.75
Ограничение по памяти, мегабайт256





Министерство обороны Флатландии планирует построить новый военный полигон. Полигон должен иметь форму круга.

Поскольку генералы в министерстве волнуются о секретности проводимых на полигоне испытаний, он должен быть надежно защищен. Флатландия защищена сверху несколькими специальными силовыми щитами, каждый из них имеет форму прямоугольника со сторонами, параллельными осям координат. Генералы хотят выбрать такое место для полигона, где он был бы полностью защищен хотя бы двумя конкретными силовыми щитами (недостаточно, чтобы каждая точка просто была защищена хотя бы двумя щитами, должно быть два щита, каждый из которых защищает полигон полностью).

Конечно, генералы хотят построить полигон максимального возможного размера. Помогите им выбрать такое место для полигона, чтобы он имел максимальный возможный радиус.

Входные данные

Первая строка входного файла содержит число \(N\) — количество силовых щитов. Каждая из следующих N строк описывает силовой щит (\(1 \leq N \leq 200000\)). Описание представляет собой четверку координат: \(x_{min}\), \(y_{min}\), \(x_{max}\), \(y_{max}\). Все координаты целые и не превышают 100000 по абсолютной величине.

Выходные данные

Выведите три вещественных числа — координаты центра полигона и его радиус. Все числа следует выводить ровно с одним знаком после десятичной точки.

Если построить полигон невозможно, выведите “Impossible” на первой строке выходного файла.

Примеры тестов
Входные данные
4
0 0 2 3
1 -1 4 1
1 1 4 4
2 0 5 5
Выходные данные
3.0 2.0 1.0
Входные данные
1
0 0 1 1
Выходные данные
Impossible
Входные данные
2 
0 0 3 3
0 0 3 3
Выходные данные
1.5 1.5 1.5
Решения, работающие при \(1 \leq N \leq 5 000\), будут набирать не менее 50 баллов
#111582
Гарри Поттер и Зал Пророчеств
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Отряд Дамблдора готовится к полёту в Отдел Тайн Министерства Магии. Так как на их пути за Пророчеством могут встретиться слуги Волан-де-Морта, Гарри с Невиллом решили потренироваться в дуэльных боях.

Они решили провести \(n\) раундов дуэли, а после каждого раунда выпивать восстанавливающее зелье, чтобы не тратить лишних сил. Всего у ребят \(2n\) зелий. После каждого раунда дуэли они выбирают два наиболее близких по мощности восстанавливающих зелья. Из нескольких таких пар они выбирают ту, у которой сумма мощностей наибольшая. Затем Невилл выпивает более мощное зелье из пары, а Гарри - менее мощное.

Помогите Гарри с Невиллом определить, какие зелья и в каком порядке выпьет каждый из них.

Формат входного файла

Первая строка входного файла содержит одно целое число \(n\) (\(1 \le n \le 100\,000\)) - количество раундов дуэли. Во второй строке входного файла содержится \(2n\) целых чисел \(a_1, a_2, \ldots, a_{2n}\) (\(1\le a_i \le 10^9\)), где \(a_i\) - мощность \(i\)-го восстанавливающего зелья.

Формат выходного файла

В первой строке выведите \(n\) чисел - мощности зелий, которые выпьет Невилл. Во второй строке выведите \(n\) чисел - мощности зелий, которые выпьет Гарри. Зелья надо выводить в том порядке, в котором Невилл и Гарри должны их выпивать.

Система оценки

Подзадача 0 (0 баллов) тесты из условия. 

Подзадача 1 (15 баллов) \( n \le 100; max(a) - min(a) \le 1000\). 

Подзадача 2 (25 баллов) \( n \le 100\). Необходимые подгруппы: 1. 

Подзадача 3 (25 баллов) \( n \le 10000\). Необходимые подгруппы: 1, 2. 

Подзадача 4 (35 баллов) Без дополнительных ограничений. Необходимые подгруппы: 1, 2, 3.

Примеры
Входные данные
1
3 6
Выходные данные
6
3
Входные данные
2
11 43 56 22
Выходные данные
22 56
11 43
#111584
Делимость на 15
  

Необходимо определить делится ли данное число на 15.

Входные данные

Натуральное число вводится своим двоичным представлением (длина числа не превышает 10000 двоичных разрядов).

Выходные данные

Выведите «YES», если делится, и «NO», если нет.

Примеры тестов

Входные данные
11110
Выходные данные
YES
Входные данные
110
Выходные данные
NO

#111585
Остаток от деления
  

Дано число в K-ичной системе счисления. Найти остаток от деления его на m.

Входные данные

В первой строке даты три натуральных числа K, n, m в десятичной системе счисления (2 ≤ K ≤ 36, 1 ≤ n ≤ 104, 2 ≤ m ≤ 109). В следующей строке дано число в K-ичной системе счисления, длина которого равна n. Число состоит либо из цифр, либо из заглавных букв латинского алфавита.

Выходные данные

Выведите остаток от деления данного числа на m (в десятичной системе счисления).

Примеры тестов

Входные данные
2 5 11
11110
Выходные данные
8
Входные данные
36 2 17
AZ
Выходные данные
4

#111586
Факториальная система счисления
  

В факториальной системе счисления основаниями являются последовательность факториалов bk = k!, и каждое натуральное число x представляется в виде:

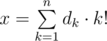, где 0 ≤ dk ≤ k

Ваша задача определить по данному в факториальной системе счисления числу его остаток от деления на p.

Входные данные

В первой строке даны два натуральных числа n и p, где n - максимальный индекс такой, что dn ≠ 0 (1 ≤ n ≤ 200, 2 ≤ p ≤ 104). Во второй строке задана последовательность dn, ..., d1, корректно определяющая некоторое натуральное число x.

Выходные данные

Выведите одно число — остаток от деления x на p.

Примеры тестов

Входные данные
5 6
1 3 3 2 1
Выходные данные
5

Примечание

В исходном примере x = 215

Страница: << 431 432 433 434 435 436 437 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест