Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 440 441 442 443 444 445 446 >> Отображать по:
#111644
Морской бой
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В рамках Чемпионата Урала планируется проведение турнира стратегий по игре «Морской бой 1D».

Игра проходит на поле, которое представляет собой прямоугольник размером 1 × N клеток. На поле расставляются T кораблей, каждый из которых имеет вид прямоугольника размером 1 × K клеток. Расстановка кораблей на поле является допустимой, если различные корабли не имеют общих клеток и разделены хотя бы одной пустой клеткой. Игровая программа осуществляет выстрелы в клетки поля, а сервер сообщает, является ли выстрел промахом или попаданием в корабль.

В процессе игры про некоторые клетки становится известно, что при любой допустимой расстановке кораблей они принадлежат какому-либо из кораблей. Назовём такие клетки заведомо занятыми.

Игра заканчивается после первого попадания в корабль. Сервер пытается добиться того, чтобы игра продолжалась как можно дольше. Для этого он не фиксирует расстановку кораблей в начале игры, а рассматривает все возможные допустимые расстановки и сообщает о попадании, только если клетка, в которую осуществляется выстрел, является заведомо занятой.

Требуется написать программу, исполняющую роль сервера для этой игры. Сервер сначала загружает параметры игры, а затем взаимодействует с игровой программой, сообщая после каждого выстрела информацию о промахе или попадании, а также количество заведомо занятых клеток.

Входные данные

Задача является интерактивной. После каждого вывода требуется сбросить буфер вывода.

Роль игровой программы исполняет программа жюри. Программа-решение исполняет роль сервера.

Первая строка стандартного ввода программы-решения содержит параметры игры — три числа: N — размер игрового поля, T — число кораблей и K — длина каждого корабля (1 ≤ N ≤ 100 000, 1 ≤ T, 1 ≤ K). Гарантируется, что на поле длины N можно по описанным правилам разместить T кораблей длины K.

После считывания параметров игры программа-решение должна определить и вывести в стандартный поток вывода количество заведомо занятых клеток.

Затем начинается игра. Программа-решение должна последовательно считывать ходы игровой программы из стандартного потока ввода и обрабатывать их следующим образом:

  1. Считать из стандартного потока ввода одно число q — номер клетки, в которую игровая программа осуществляет выстрел (1 ≤ q ≤ N). Игровая программа никогда не делает два выстрела в одну и ту же клетку.
  2. Если клетка q является заведомо занятой, вывести в стандартный поток вывода число 1 и завершить работу.
  3. Если клетка q не является заведомо занятой, вывести в стандартный поток два числа, разделенных пробелом: 0 и количество заведомо занятых клеток после этого выстрела. После этого программа-решение переходит к пункту 1 и продолжает взаимодействие с игровой программой.

Выходные данные

Примечание

Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы успешно пройдены.

  1. Тесты из условия. Подзадача оценивается в 0 баллов.
  2. N ≤ 15. Подзадача оценивается в 30 баллов.

  3. N ≤ 3000. Подзадача оценивается в 30 баллов.

  4. N ≤ 100 000. Подзадача оценивается в 40 баллов.

Примеры
Входные данные
8 2 3
4
1
Выходные данные
4
0 5
1
#111647
Списки по классам
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Входные данные

В каждой строке сначала записан номер класса (число, равное 9, 10 или 11), затем (через пробел) — фамилия ученика.

Выходные данные

Необходимо вывести список школьников по классам: сначала всех учеников 9 класса, затем — 10, затем — 11. Внутри одного класса порядок вывода фамилий должен быть таким же, как на входе.

Примеры
Входные данные
9 Ivanov
10 Petrov
11 Sidorov
9 Grigoryev
9 Sergeev
10 Yakovlev
Выходные данные
9 Ivanov
9 Grigoryev
9 Sergeev
10 Petrov
10 Yakovlev
11 Sidorov
#111648
Шарики
  
Темы: [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В одной компьютерной игре игрок выставляет в линию шарики разных цветов. Когда образуется непрерывная цепочка из трех и более шариков одного цвета, она удаляется из линии. Все шарики при этом сдвигаются друг к другу, и ситуация может повториться.

Напишите программу, которая по данной ситуации определяет, сколько шариков будет сейчас уничтожено. Естественно, непрерывных цепочек из трех и более одноцветных шаров в начальный момент может быть не более одной.

Входные данные

Даны количество шариков в цепочке (не более 10 5 ) и цвета шариков (от 0 до 9, каждому цвету соответствует свое целое число).

Выходные данные

Требуется вывести количество шариков, которое будет уничтожено.

Примеры
Входные данные
5 1 3 3 3 2
Выходные данные
3
Входные данные
10 3 3 2 1 1 1 2 2 3 3
Выходные данные
10
#111649
Длина кратчайшего пути
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В неориентированном графе требуется найти длину минимального пути между двумя вершинами.

Входные данные

Первым на вход поступает число N –– количество вершин в графе ( 1 ≤ N ≤ 100 ). Затем записана матрица смежности (0 обозначает отсутствие ребра, 1 –– наличие ребра). Далее задаются номера двух вершин –– начальной и конечной.

Выходные данные

Выведите L –– длину кратчайшего пути (количество ребер, которые нужно пройти). Если пути не существует, выведите одно число - 1 .

Примеры
Входные данные
5
0 1 0 0 1
1 0 1 0 0
0 1 0 0 0
0 0 0 0 0
1 0 0 0 0
3 5
Выходные данные
3
#111652
Купе
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Два юных шамана Егор и Саша отправились на Всероссийский Конкурс Опытных Шаманов Профессионалов. До места проведения ВКОШП можно добраться только на поезде. Всего в вагоне поезда восемь купе по четыре места в каждом. Схема нумерации мест первого купе представлена на рисунке.

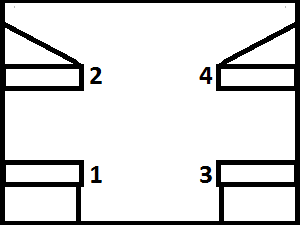
Вам известны номера мест Егора и Саши. В данный момент друзья находятся на перроне и хотят узнать, попадут ли они в одно купе и на каких полках (верхних или нижних) будут ехать.

Входные данные

В единственной строке содержатся два натуральных числа — номера мест Саши и Егора соответственно. Гарантируется, что они не будут превышать количество мест в вагоне, описанном в условии. Также гарантируется, что у Егора и Саши билеты на разные места.

Выходные данные

В первой строке выведите "YES", если друзья попадут в одно купе, и "NO" — иначе. Во второй строке выведите "LOW", если Саша будет ехать на нижнем месте, и "HIGH", если на верхнем. В третьей строке выведите положение места Егора в том же формате

Примечание

В этой задаче всего 50 тестов, каждый оценивается в 2 балла независимо от других.

Примеры
Входные данные
1 2
Выходные данные
YES
LOW
HIGH
Входные данные
1 5
Выходные данные
NO
LOW
LOW
Страница: << 440 441 442 443 444 445 446 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест