Два юных шамана Егор и Саша отправились на Всероссийский Конкурс Опытных Шаманов Профессионалов. До места проведения ВКОШП можно добраться только на поезде. Всего в вагоне поезда восемь купе по четыре места в каждом. Схема нумерации мест первого купе представлена на рисунке.
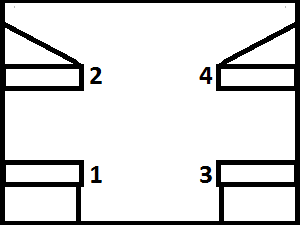
Вам известны номера мест Егора и Саши. В данный момент друзья находятся на перроне и хотят узнать, попадут ли они в одно купе и на каких полках (верхних или нижних) будут ехать.
В единственной строке содержатся два натуральных числа — номера мест Саши и Егора соответственно. Гарантируется, что они не будут превышать количество мест в вагоне, описанном в условии. Также гарантируется, что у Егора и Саши билеты на разные места.
В первой строке выведите "YES", если друзья попадут в одно купе, и "NO" — иначе. Во второй строке выведите "LOW", если Саша будет ехать на нижнем месте, и "HIGH", если на верхнем. В третьей строке выведите положение места Егора в том же формате
В этой задаче всего 50 тестов, каждый оценивается в 2 балла независимо от других.
1 2
YES LOW HIGH
1 5
NO LOW LOW
Прямо с вокзала Егор и Саша отправились на открытие ВКОШП. Так как они прибыли позже всех, то им достались места в последнем ряду.
Вдруг друзья заметили, что все участники, которые сидят перед ними, рассматривают на своих ноутбуках Pinebook разные фрагменты одной большой картинки. Друзьям стало интересно, что это за картинка. К счастью, Егор совершенно случайно взял с собой пульт PineappleRemote, с помощью которого можно обменять фрагменты картинки между двумя любыми компьютерами. Естественно, при этом могут возмущаться владельцы этих компьютеров, поэтому Саша и Егор хотят, чтобы количество обменов не превышало пяти миллионов.
Перед ними расположены n рядов по m мест, на каждом из которых есть ноутбук с фрагментом картинки. Саша поставил в соответствие каждому фрагменту номер таким образом, что:
- все номера различны;
- если расставить все фрагменты в порядке возрастания номеров в n рядов по m штук, то получится целостная картинка.
Но, к сожалению, праздничная церемония, оригинальная музыка и блестящие ведущие так понравились друзьям, что они подумали: "Кто, если не Вы сможете составить список действий, после которых на Pinebook-ах они смогут увидеть картинку целиком?".
В первой строке находятся два натуральных числа n и m — количество рядов и количество мест в каждом из них. Далее идут n строк по m чисел в каждом: j-ое число на i-ой строке является номером фрагмента на ноутбуке, стоящем на j-ом месте i-ого ряда.
В первой строке выведите число c (0 ≤ c ≤ 5000000) — количество обменов фрагментов изображения между ноутбуками, которые необходимо произвести. Следующие c строк должны содержать информацию о совершенных обменах. В i строке выведите четыре натуральных числа: x1, y1, x2, y2 (1 ≤ x1, x2 ≤ n;1 ≤ y1, y2 ≤ m) — номера рядов и мест компьютеров, между которыми происходит i-ый по счету обмен. Вывод двух одинаковых позиций (x1 = x2 и y1 = y2) будет расцениваться как неправильный ответ!
Если существует несколько правильных ответов, выведите любой из них.
Пояснение к первому тесту: 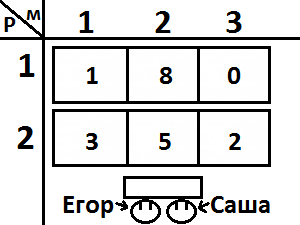
Тесты в этой задаче состоят из пяти групп:
2 3 1 8 0 3 5 2
3 1 1 1 3 1 2 2 3 1 2 1 3
1 1 42
0
После открытия, как это обычно бывает, всех участников ведут на экскурсию. Естественно, Олимпиада Шаманов-Профессионалов — не исключение.
Проезжая мимо очередной местной достопримечательности, Егор вспомнил, как весело было на сборах перед олимпиадой. Помнится, в один день им пришлось решать целых десять задач! Но, не растерявшись, Егор определил, что он точно решит все задачи с первой по третью, Саша без раздумий принялся за четвертую, пятую и шестую задачи, Андрей к концу дня справился со всеми задачами с седьмой по девятую, а Стёпа смог решить самую сложную десятую задачу.
После того, как Егор поделился воспоминаниями с Сашей, тот сразу же сформулировал задачу: а если бы ребят было не четверо, а N человек, и задач предлагалось M? Пусть тогда каждый сразу определил, что он решит все задачи с bi по ei, но не сможет сделать ни одной другой. Смогут ли они вместе решить все задачи, или же найдется такая, которая никому не по зубам?
От нечего делать Егор призадумался: а как же решить такую задачу?
В первой строке содержатся два натуральных числа N и M — количество участников и задач соответственно. Далее следуют N строк по два натуральных числа bi и ei в каждой (1 ≤ si ≤ ei ≤ M), которые означают, что i-ый участник решит все задачи с bi-ой по ei-ую.
В единственной строке выведите "YES", если участники справятся со всеми задачами, или "NO" в противном случае.
Тесты в этой задаче состоят из шести групп:
2 10 1 4 3 10
YES
2 10 1 9 2 9
NO
По результатам отборочных туров Саша и Егор прошли в финал. Отдыхая в гостинице, Егор случайно нашел на сайте олимпиады одну из задач предстоящего финала:
«Вам дана таблица размера N × M. Ваша задача — определить, встречается ли заданное слово в таблице. Считается, что в таблице встречается слово, если мы можем найти последовательно все его буквы, начав с какой-то клетки таблицы, и переходя от одной клетки таблицы к соседней по вертикали или горизонтали, при этом нельзя посещать одну клетку несколько раз.»
Егор и Саша знают, что если они попытаются решить эту задачу перед туром, их заметит Страшное Око Истребления и они будут тотчас же дисквалифицированы. Но зато Вам ничего не грозит, поэтому, ребята просят Вас помочь им, хотя и понимают, что это немного нечестно.
В первой строке содержатся два натуральных числа N и M — размеры таблицы. В следующих N строках содержатся по M символов — сама таблица. Далее идет строка с единственным натуральным числом L — длиной искомого слова. В последней строке записано заданное слово. Все символы в таблице и в слове являются строчными (маленькими) латинскими буквами. Все числа не превосходят 10.
В единственной строке выведите "YES" (без кавычек), если заданное слово встречается в таблице, и "NO" (без кавычек) в противном случае.
В этой задаче всего 10 тестов, каждый оценивается в 10 баллов независимо от других.
4 5 aaaaa aaaaa aaaaa aaaaa 5 lordf
NO
3 3 ale zsx ccs 5 alexs
YES
Спустя 2 месяца после олимпиады друзья получили письмо от организаторов ВКОШП с предложением составить задачи на следующий год! С тех пор молодые шаманы регулярно обмениваются своими задачами.
Саша предложил Егору следующую задачу: «В один ряд выложены N карточек, на каждой из которых написано целое положительное число. Кирилл и Семён начинают по очереди забирать карточки. Разрешается брать только первую или последнюю карточку ряда. Кирилл берет первым. Число, записанное на карточке, добавляется к очкам игрока. Кирилл в последнее время очень занят, потому что он недавно устроился работать программистом в компанию, занимающуюся прокладкой туннелей в Европе. Поэтому ему некогда продумывать стратегию предстоящей игры и он просит Вас определить максимальную сумму, которую он может получить, при условии, что Семён играет оптимально.»
Егор быстро решил эту задачу, а Вы справитесь?
В первой строке содержится единственное натуральное число N — количество карточек в последовательности. Во второй строке содержится N чисел, записанных на карточках.
Выведите единственное число — максимальную сумму, которую может получить Кирилл.
Тесты в этой задаче состоят из четырех групп:
1 1
1
5 1 2 5 2 1
5