Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Миша записывает 2 числа: n и m, а Маша должна разделить число n на m частей, не меняя порядок цифр, при этом Миша ещё требует, чтобы произведение полученных m чисел было максимально. Помогите Маше.
Входные данные содержат несколько тестовых случаев (не более 100000). Каждый тестовый случай расположен в отдельной строке и содержит 2 числа, разделённые пробелом: сначала n (1 ≤ n ≤ 1015), а потом m (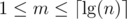 ).
).
Для каждого тестового примера в отдельной строке выведите искомое максимальное произведение.
12345 2 12345 3
6170 2460
Одной из классических NP-полных задач является так называемая «Задача о рюкзаке». Формулируется она следующим образом. Дано n предметов, каждый из которых характеризуется весом wi и полезностью pi. Необходимо выбрать некоторый набор этих предметов так, чтобы суммарный вес этого набора не превышал W, а суммарная полезность была максимальна. Ваша задача состоит в том, чтобы написать программу, решающую задачу о рюкзаке.
Первая строка входного файла содержит натуральные числа n(1 ≤ n ≤ 20) и W(1 ≤ W ≤ 109). Каждая из последующих n строк содержит описание одного предмета. Каждое описание состоит из двух чисел: wi — веса предмета и pi — его полезности (1 ≤ wi, pi ≤ 109).
В первой строке выходного файла выведите количество выбранных предметов и их суммарную полезность. Во второй строке выведите через пробел их номера в возрастающем порядке (предметы нумеруются с единицы в порядке, в котором они перечислены во входном файле). Если искомых наборов несколько, выберите тот, в котором наименьшее число предметов. Если же после этого ответ по-прежнему неоднозначен, выберите тот набор, в котором первый предмет имеет наименьший возможный номер, из всех таких выберите тот, в котором второй предмет имеет наименьший возможный номер, и т. д.
2 10 10 100 9 80
1 100 1
5 100 80 1000 50 550 50 550 50 550 50 550
2 1100 2 3
6 100 80 1000 50 550 50 550 50 550 50 550 100 1100
1 1100 6
Вася устроился сисадмином в крупную и известную компанию Проблемсофт. В сети компании n компьютеров, некоторые пары которых соединены кабелем напрямую. Всего таких соединений m, причем Вася весьма неплохой администратор, так что никакой кабель не соединяет компьютер с самим собой и каждая пара компьютеров соединена не более чем одним кабелем.
На каждом компьютере в фирме Проблемсофт установлена специальная программа разработанная и поддерживаемая инженерами Проблемсофта, под названием ЗлойЖук. Инженеры этой компании отличаются крайним трудолюбием и высокой производительностью, в связи с чем новые версии программы ЗлойЖук выходят почти ежедневно. Однако, не все сотрудники компании разделяют трудолюбие инженеров, поэтому обновляют программу ЗлойЖук неохотно, и всякий раз до какой-то случайной версии (вполне могут "обновить" до такой же или даже более старой).
После нескольких ужасных месяцев, в течение которых исправлять различные ошибки приходилось днями и ночами, без обедов и выходных, Вася понял в чем причина подавляющего большинства всех сбоев! Причина в том, что компьютеры пересылающие данные по соединяющему их кабелю могут иметь различные версии программы ЗлойЖук. Прямое соединение кабелем двух компьютеров с различными версиями программы ЗлойЖук Вася называет нестабильным.
На последнем корпоративе компании Проблемсофт Вася вместо развлечений ходил с листочком и узнавал у каждого сотрудника когда он планирует обновить программу ЗлойЖук и до какой версии. Нельзя сказать, чтобы коллеги охотно отвечали на эти вопросы, вместо того что купаться в джакузи и пить Кока-Колу, но все-таки Вася смог составить график планируемых изменений версий программы ЗлойЖук на всех компьютерах сети Проблемсофта. Теперь его интересует количество нестабильных соединений в сети после выполнения каждого изменения.
Первая строка входного файла содержит два целых числа n и m (1 ≤ n, m ≤ 105).
Вторая строка содержит n целых чисел v1, v2, ..., vn: версии программы ЗлойЖук изначально установленные на компьютерах Проблемсофта (1 ≤ vi ≤ 105).
Следующие m строк содержат числа ai и bi: описание соединений (1 ≤ ai, bi ≤ n, ai ≠ bi). Гарантируется что сеть хорошая, то есть никакая пара компьютеров не соединена более чем одним кабелем и никакой компьютер не соединен кабелем с самим собой.
Следующая строка содержит целое число q: количество запланированных изменений версий программы ЗлойЖук (1 ≤ q ≤ 105).
Далее следуют q строк; i-ая содержит числа ci и v'i: номер компьютера на котором происходит изменение, и номер новой версии программы ЗлойЖук. Изменения даны в хронологическом порядке, никакия два изменения не происходят одновременно.
Выведите q строк; i-ая строка должна содержать одно целое число: количество нестабильных соединений сразу после выполнения i-го обновления.
4 5 1 2 3 4 1 2 2 3 3 4 4 1 1 3 5 1 5 3 2 4 4 1 4 2 3
5 4 4 3 4
Задано подвешенное дерево, содержащее n (1 ≤ n ≤ 100 000) вершин, пронумерованных от 0 до n - 1. Требуется ответить на m (1 ≤ m ≤ 10 000 000) запросов о наименьшем общем предке для пары вершин. Запросы генерируются следующим образом. Заданы числа a1, a2 и числа x, y и z. Числа a3, ..., a2m генерируются следующим образом: ai = 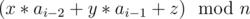 . Первый запрос имеет вид {a1, a2}. Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид {
. Первый запрос имеет вид {a1, a2}. Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид {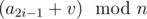 , a2i}.
, a2i}.
Первая строка содержит два числа: n и m. Корень дерева имеет номер 0. Вторая строка содержит n - 1 целых чисел, i-е из этих чисел равно номеру родителя вершины i. Третья строка содержит число содержит два целых числа в диапазоне от 0 до n - 1: a1 и a2. Четвертая строка содержит три целых числа: x, y и z, эти числа неотрицательны и не превосходят 109.
Выведите в выходной файл сумму номеров вершин — ответов на все запросы.
3 2 0 1 2 1 1 1 0
2
Последнее время на подъездах в Нижнем Новгороде стало популярно ставить домофоны. Домофон представляет собой цифровую клавиатуру, на которой посетитель должен набрать номер нужной ему квартиры и нажать клавишу вызова, после чего жители этой квартиры могут открыть ему дверь (а могут и не открыть).
При интенсивном использовании домофона краска, нанесённая на цифровые клавиши, постепенно стирается. Одна из компаний, занимающихся установкой домофонов, заинтересовалась возможностью определить диапазон номеров квартир, расположенных в подъезде, по тому, насколько стёрлась краска с клавиш. Они уже обнаружили, что по состоянию клавиши можно определить, сколько раз эту клавишу нажимали. Теперь вам, программисту этой компании, поручили для начала решить простейший вариант задачи восстановления диапазона квартир по «затёртостям». А именно, вашей программе на вход даются 10 чисел — «затёртости» клавиш 0, 1, ..., 9, т. е. количество раз, которое нажималась соответствующая клавиша. Считая, что за время использования домофона каждую квартиру набрали ровно один раз, и считая, что номера квартир в подъезде начинаются с 1 (т. е. в подъезде расположены квартиры с номерами 1, 2, ..., N при некотором N), определите диапазон квартир в этом подъезде (т. е., фактически, определите это N). Считайте, что посетители никогда не набирают ведущих нулей. Считайте, что N не может превосходить 109.
На первой строке входного файла находятся 10 чисел затёртости цифр 0, 1, ..., 9. Все затёртости не превышают 109; гарантируется, что есть хотя бы одна ненулевая затёртость.
В выходной файл выведите одно число N. Если подходящего набора диапазона квартир не существует, выведите одно число - 1. Если подходящих N существует несколько, выведите любое. Гарантируется, что, если искомое N существует, то оно не превосходит 109.
1 2 1 1 1 1 1 1 1 1
10
2 4 2 2 2 2 2 2 2 2
-1
1 1 0 0 0 0 0 0 0 0
-1
1 0 0 0 0 0 0 0 0 0
-1
162 273 270 263 263 263 263 262 189 162
826