Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Фирма, в которой работает ваш друг, недавно провела рекламную акцию «Сфотографируй маршрутку — получи приз», в рамках которой пассажиры могли присылать свои фотографии маршруток этой фирмы, а потом специальная конкурсная комиссия выбирала из них лучшие и награждала победителей. Теперь организаторы собираются выставить все фотографии на сайт фирмы.
При подготовке фотографий возникла одна проблема: видимо, некоторые пассажиры фотографировали маршрутки наспех, и потому некоторые фотографии оказались перекошенными: те линии, которые по идее должны быть горизонтальными, оказались наклонными (см. рис.). Администратор сайта категорически отказался выставлять такие фотографии на сайт, порекомендовав организаторам повернуть и обрезать фотографии так, чтобы горизонтальные линии стали на самом деле горизонтальными.
Поэтому организаторы провели большую работу и для каждой фотографии определили, под каким углом на фотографии наклонён горизонт. Теперь им надо вырезать из фотографии прямоугольник, у которого две стороны были бы параллельны горизонту, а две другие, конечно, перпендикулярны. Организаторы хотели вырезать прямоугольник наибольшей возможной площади, удовлетворяющий этому условию, но администратор сайта упростил им работу, потребовав сохранить отношение сторон фотографии. Таким образом, им теперь надо из каждой фотографии вырезать прямоугольный кусок со сторонами, параллельными и перпендикулярными горизонту, и с тем же отношением сторон, что и у оригинальной фотографии, причём среди всех таких прямоугольников выбрав наибольший по площади.
Зная вашего друга не только как хорошего экономиста, но и человека со связями, они обратились к нему с просьбой найти программу, которая помогла бы им выбрать нужный прямоугольник. Ваш друг перенаправил эту просьбу к вам.
Обратите внимание, что порядок сторон администратору сайта важен: если на оригинальной фотографии ширина была w, а высота h, а у найденного прямоугольника ширина (т. е. сторона, параллельная горизонту)w , а высота (т. е. вторая сторона) h, то должно быть 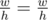 , а не
, а не 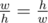 .
.
Во входном файле находятся три вещественных числа: w, h и α — размеры оригинальной фотографии (ширина, высота) и угол наклона горизонта к ширине в градусах (см. рис.). Гарантируется, что 0 ≤ w ≤ 100, 0 ≤ h ≤ 100, - 90 ≤ α ≤ 90. Положительные α обозначают, что горизонт получается из ширины фотографии поворотом против часовой стрелки (как на рисунке), отрицательные α — по часовой стрелке.
В выходной файл выведите одно число — площадь искомого прямоугольника. Ваш ответ должен отличаться от правильного не более чем на 10 - 4.
4 3 30
5.1082415465
4 3.0 0
12.0000000000
4 3 90.0
6.7500000000
Написать рекурсивную программу перевода целых чисел, не превосходящих 109, из десятичной системы счисления в P-ичную (1 ≤ P ≤ 36)
В первой строке вводится значение P, во второй строке — число, которое надо перевести.
Цифры, участвующие в записи числа в P-ичной системе счисления, соответствующие десятичным числам 10, 11, ..., P - 1, заменять на заглавные латинские буквы А, В, С, ... . Вывод осуществлять следующим образом: сначала выводится число в десятичной системе счисления(введённое), за ним система счисления, в которой оно записано, в круглых скобках, затем ставится знак "=" и аналогично выводится результат работы Вашей программы — число в P-ичной системе счисления. Весь вывод осуществляется без пробелов.
3 123
123(10)=11120(3)
На вход программе подаются 3 целых неотрицательных числа x, N и P, не превосходящих 2 * 109. Кроме того P > 0. Требуется вычислить значение x в степени N по модулю P.
2 10 1000
24
Петя с Андреем играют в интересную игру. Для этой игры им необходимо k шоколадок, каждая из которых имеет форму прямоугольника i-ая из них имеет размер wi на hi долек.
Петя с Андреем ходят по очереди, за один ход игрок должен взять со стола одну шоколадку, разломать ее на две неравных непустых части, и их обе положить обратно на стол. При этом обе получающиеся части должны иметь форму прямоугольника, длины сторон которого выражаются целым числом долек.
Первый ход в этой игре делает Петя. Проигрывает игрок, который не может сделать ход. Победитель после этого получает весь шоколад, лежащий на столе.
Ваша задача — определить, кто из игроков выиграет при оптимальной игре обоих.
Входной файл содержит несколько наборов входных данных. Первая строка входного файла содержит количество T наборов входных данных (1 ≤ T ≤ 1000).
Каждый набор входных данных описывается следующим образом. Первая строка описания содержит число k (1 ≤ k ≤ 100) — количество шоколадок, лежащих на столе в начале игры. Последующие k строк описывают шоколадки: i-ая из этих строк содержит два числа: wi и hi — размеры соответствующей шоколадки (1 ≤ wi, hi ≤ 100).
Для каждого набора входных данных выведите ответ. Следуйте формату, приведенному в примерах.
3 1 1 1 1 3 1 2 1 1 3 1
Game 1: Andrew wins. Game 2: Petr wins. Game 3: Petr wins.
Рассмотрим последовательность n целых чисел от 1 до m. Подпоследовательность подряд идущих чисел называется рефреном, если произведение ее длины на количество вхождений в последовательность максимально.
По заданной последовательности требуется найти ее рефрен.
Первая строка входного файла содержит два целых числа: n и m (1 ≤ n ≤ 150 000, 1 ≤ m ≤ 10).
Вторая строка содержит n целых чисел от 1 до m.
Первая строка выходного файла должна содержать произведение длины рефрена на количество ее вхождений. Вторая строка должна содержать длину рефрена. Третья строка должна содержать последовательность которая является рефреном.
9 3 1 2 1 2 1 3 1 2 1
9 3 1 2 1