Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Рассмотрим один специальный тип двоичных деревьев поиска, который часто называют "декартовым деревом". Напомним, что двоичным деревом поиска называется двоичное дерево, в каждой вершине которого записан некоторый ключ (в этой задаче ключ представляет собой целое число), причем для каждой вершины
u
выполнены следующие условия: все ключи в левом поддереве
u
меньше чем ключ в вершине
u
, а все ключи в правом поддереве - больше. Будем называть двоичное дерево поиска декартовым деревом, если в каждой вершине
u
помимо основного ключа
х
u
хранится также вспомогательный ключ
y
u
, причем для этих ключей выполнено "условие кучи": если
v
- родитель
u
, то
y
v
<
y
u
. Будем называть множество пар
(
x
1
,
y
1
), (
х
2
,
y
2
), ... (
х
n
,
у
n
)
корректным
, если все
x
i
– различные числа от 1 до
n
, и то же условие выполнено для
y
i
. Легко показать, что для любого корректного множества пар существует в точности одно декартово дерево, которое содержит пары из заданного множества в качестве пар ключей. Рассмотрим двоичное дерево
T
с
n
вершинами. Ваша задача - найти количество различных корректных множеств пар, таких что их можно расставить в вершинах
T
. чтобы превратить его в декартово дерево. Например, для дерева, приведенного на рисунке, существует три соответствующих корректных множества пар:
{(1, 2), (2, 3), (3, 1), (4, 4)}, {(1, 2), (2, 4), (3, 1), (4, 3)}
и
{(1, 3), (2, 4), (3, 1), (4, 2)}.

Первая строка входного файла содержит n – количество вершин в дереве T (1 ≤ n ≤ 200) следующие n строк описывают его вершины. Каждая вершина описывается двумя числами: номерами левого и правого ребёнка. Если один из детей отсутствует, то вместо его номера указан 0. Гарантируется, что описание дерева корректно. Корень дерева имеет номер 1.
Выведите одно число – количество различных корректны множеств пар, которые можно расставить в вершинах T , чтобы получилось декартово дерево.
4 2 3 0 4 0 0 0 0
3
В подвале вновь построенного здания на потолке расположен сильный источник света. К сожалению, покрытие на полу очень чувствительно к свету и разрушается под его воздействием. Чтобы этого избежать было решено защитить покрытие от света, однако сделать это не легко, т.к. в подвале проходит много труб и если они уже загораживают часть пола от света, то соответствующие участки было решено дополнительно не защищать.
Поиск решения можно проводить с помощью двухмерной модели. В этой модели ось Ох расположена на уровне пола, источник света считается точкой с целочисленными координатами ( b x , b y ) . Трубы представляют собой окружности. Центр i -й окружности имеет целочисленные координаты ( с x , c y ) , радиус r i также целый. Так как трубы сделаны из твердого материала, окружности не пересекаются. Трубы не отражают и не пропускают свет. Вы должны написать программу, которая найдет непересекающиеся интервалы на оси Ох , которые уже защищены от света благодаря имеющимся трубам.
Входной файл состоит из набора сразу нескольких тестов. Общее число строк в файле не превосходит 20000 . В первой строке каждого теста содержится положительное целое число N ≤ 10000 — обозначающее количество труб. Во второй строке расположены два целых числа b x и b y , разделенных пробелом. Каждая из следующих N строк содержит 3 целых числа через пробел с x , c y и r i , причем c y + r i < b y . Последний тест содержит единственную строку, содержащую N = 0 .
Для каждого теста выведите набор искомых интервалов по одному в строке. Интервал описывается двумя вещественными координатами. Ответ будет считаться правильным, если его относительная и абсолютная погрешности не будут превосходить \(10^{-6}\). Интервалы должны быть отсортированы в порядке возрастания координаты x . В конце каждого набора интервалов выводите пустую строчку.
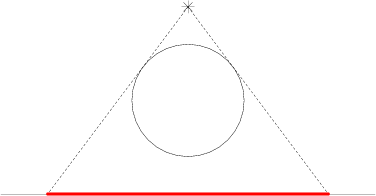
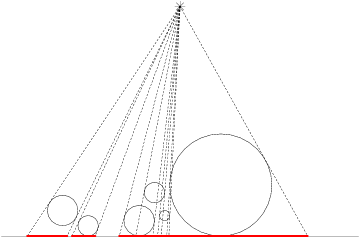
Картинки иллюстрируют тест из условия.
1 300 300 300 150 90 6 300 450 70 50 30 120 20 20 270 40 10 250 85 20 220 30 30 380 100 100 0
75.00 525.00 0.72 78.86 88.50 133.94 181.04 549.93
Андрей Сергеевич работает воспитателем в детском саду. Недавно он придумал новую веселую игру, для участия в которой все дети разбились на n команд. В качестве призов для участников игры Андрей Сергеевич подготовил d конфет.
По итогам игры оказалось, что в команде, занявшей i -е место, ровно x i участников.
Теперь перед Андреем Сергеевичем стоит непростая задача: надо распределить конфеты. При этом должны выполняться следующие условия:
Первая строка содержит два целых числа n и d ( 1 ≤ n ≤ 100 , 1 ≤ d ≤ 10 6 ). Вторая строка содержит n целых чисел x 1 , ..., x n ( 1 ≤ x i ≤ 100 для всех i от 1 до n ).
Если разделить конфеты возможно, то в первой строке выведите YES , а во второй выведите n целых чисел: a 1 , a 2 , ..., a n . Если разделить конфеты указанным способом нельзя, выведите NO .
2 100 2 1
YES 49 2
2 6 2 1
NO
Алла очень любит палиндромы. Все потому, что её имя является палиндромом. Напомним, что строку называют палиндромом тогда, когда она одинаково читается как слева направо, так и справа налево.
Однажды в школе учитель рассказал Алле про так называемые строки Фибоначчи. Строки Фибоначчи определяются следующим образом:
Аллу сразу заинтересовал вопрос — какой максимально длинный палиндром встречается в k -й строке Фибоначчи. Помогите Алле решить эту задачу.
Первая строка входного файла содержит одно целое число k (0 ≤ k ≤ 80) — номер строки Фибоначчи.
В выходной файл выведите длину самого большого палиндрома, содержащегося в k -й строке Фибоначчи.
2
1
4
4
В этой задаче Вам требуется найти максимальную по длине подстроку данной строки, такую что каждый символ встречается в ней не более k раз.
В первой строке даны два целых числа n и k (1 ≤ n ≤ 100000, 1 ≤ k ≤ n ) , где n – количество символов в строке. Во второй строке n символов – данная строка, состоящая только из строчных латинских букв.
В выходной файл выведите два числа – длину искомой подстроки и номер её первого символа. Если решений несколько, выведите любое.
3 1 abb
2 1
5 2 ababa
4 1