Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 479 480 481 482 483 484 485 >> Отображать по:
#112561
Весы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

Если в продаже нет стандартного набора гирь, измерение массы становится большой проблемой. Ваш набор содержит n гирь массой 1 грамм, 4 грамма, 16 грамм, ..., 4 n - 1 грамм. Кроме того, у вас есть две чаши весов. Чтобы взвесить объект, надо положить его на левую чашу весов и поставить некоторые гири на левую и правую чашу для достижения равновесия. Требуется найти, сколько целых масс в диапазоне [1; m ] возможно измерить, используя весы и данный набор гирь.

Входные данные

В единственной строке содержаться 2 целых числа m и n (1 ≤ n , m ≤ 10 9 ) .

Выходные данные

Выведите одно число - количество масс, которые можно измерить с помощью этих гирь.

Примеры
Входные данные
1 5
Выходные данные
1
Входные данные
5 7
Выходные данные
4
#112566
Пивная
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В городе, являющемся одним из ведущих Российских образовательных центров, решили построить пивную. Естественно, что ректоры находящихся в городе ВУЗов потребовали, чтобы пивная была максимально удалена от каждого из ВУЗов. Помогите директору будущей пивной выбрать оптимальное место для строительства. Граница города представляет собой выпуклый многоугольник. Положение ВУЗов задается координатами точек внутри этого многоугольника. Пивную нужно построить так, чтобы расстояние от нее до ближайшего вуза было максимально. Пивную можно строить как внутри города, так и на его границе.

Входные данные

В первой строке потока ввода задается число \(3 \le N \le 10\) – количество вершин многоугольника, являющегося границей города. В следующей строке – \(2*N\) вещественных чисел по модулю не превосходящих 1000, являющихся координатами вершин многоугольника, перечисленными в порядке обхода границы города против часовой стрелки. Никакие две вершины многоугольника не совпадают, никакие три не лежат на одной прямой. В третьей строке потока ввода находится число \(1 \le M \le 100\) – количество ВУЗов в городе. В следующей строке – \(2 * M\) вещественных чисел по модулю не превосходящих 1000, являющихся координатами каждого из ВУЗов(никакие два ВУЗа не расположены в одной точке).

Выходные данные

В первую строку выходного потока вывести минимальное расстояние от планируемого места строительства пивной до ближайшего к ней ВУЗа. Во второй строке вывести через пробел координаты места, оптимального для строительства пивной. Результаты выводить с двумя цифрами после точки.

Примечание

Все вещественные числа задаются не более чем с двумя значащими цифрами после точки.

Примеры
Входные данные
3
0 0 4 1 0 3
1
1 1
Выходные данные
3.00
4.00 1.00
#112567
Кубики
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Привидение Петя любит играть со своими кубиками. Он любит выкладывать их в ряд и разглядывать свое творение. Однако недавно друзья решили подшутить над Петей и поставили в его игровой комнате зеркало. Ведь всем известно, что привидения не отражаются в зеркале! А кубики отражаются. Теперь Петя видит перед собой N цветных кубиков, но не знает, какие из этих кубиков настоящие, а какие — всего лишь отражение в зеркале. Помогите Пете! Выясните, сколько кубиков может быть у Пети. Петя видит отражение всех кубиков в зеркале и часть кубиков, которая находится перед ним. Часть кубиков может быть позади Пети, их он не видит.

Входные данные

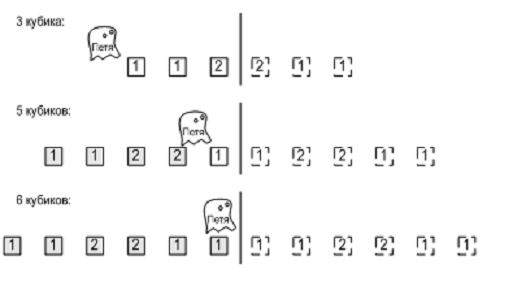
Первая строка входного файла содержит число N ( 1 ≤ N ≤ 1000000 ) и количество различных цветов, в которые могут быть раскрашены кубики — M ( 1 ≤ M ≤ 1000000 ). Следующая строка содержит N целых чисел от 1 до M — цвета кубиков.

Выходные данные

Выведите в выходной файл все такие K , что у Пети может быть K кубиков

Примеры
Входные данные
6 2
1 1 2 2 1 1
Выходные данные
3 5 6
#112571
НЛО
  
ограничение по времени на тест
0.25 second;
ограничение по памяти на тест
64 megabytes

В маленьком городке М начала действовать служба контроля за незаконными полетами НЛО. Первая задача службы — выяснить, сколько НЛО действует в окрестности города. Агенты службы опросили множество свидетелей и составили список случаев встречи с НЛО, произошедших за одни сутки, с указанием места и времени наблюдения. Теперь аналитики хотят понять, сколько же на самом деле было НЛО. Из данных разведки известна максимальная скорость, с которой может лететь НЛО. Аналитики просят вас узнать, какое минимальное количество НЛО могли наблюдать свидетели.

Входные данные

На первой строке входного файла содержатся целые числа n и v — количество случаев наблюдения и максимальная скорость НЛО ( 1 ≤ n ≤ 100 , 1 ≤ v ≤ 10000 ). Следующие n строк содержат описания случаев встречи с НЛО в формате «ЧЧ:ММ x y», где ЧЧ:ММ — время встречи, x и y — координаты места, в котором наблюдался НЛО (для простоты будем считать, что все встречи происходили на плоскости). Координаты по модулю не превышают 1000 . Скорость выражена в км/ч, координаты — в км.

Выходные данные

Выведите в выходной файл одно число — минимальное возможное количество НЛО.

Примеры
Входные данные
4 1
12:00 0 0
13:10 0 1
14:00 1 0
15:00 1 1
Выходные данные
2
#112573
Data Packing
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes

Адам, будучи организованным человеком, всегда любит порядок. Иногда он любит вспоминать, как когда-то проводил долгие часы за компьютером, перенося данные на диски.

Есть два важных правила хранения данных на дисках: Адам никогда не хранит более двух файлов на одном диске (это нужно, чтоб ему было проще их подписывать), он никогда не делит файл на части. Но диски достаточно большие, чтобы уместить любой файл.

Адам использует диски одного размера. Помогите ему разместить файлы, в соответствии с правилами, используя минимальное количество дисков.

1 ≤ T ≤ 100. 1 ≤ X ≤ 700. 1 ≤ S i ≤ X .

В задаче есть две группы тестов: 1. 1 ≤ N ≤ 10 - оценивается в 40 баллов 2. 1 ≤ N ≤ 1 4 - оценивается в 60 баллов

Входные данные

Первая строка входного файла содержит число N - количество файлов и X - ёмкость одного диска. Во второй строке дано N чисел S i - размеры файлов.

Выходные данные

Выведите одно число - минимальное количество дисков, умещающих все файлы по правилам.

Примеры
Входные данные
3 100
10 20 70
Выходные данные
2
Входные данные
4 100
30 40 60 70
Выходные данные
2
Входные данные
5 100
10 20 30 40 60
Выходные данные
3
Страница: << 479 480 481 482 483 484 485 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест