Флатландский валун имеет форму многоугольника (не обязатеьно выпуклого). Для простоты будем рассматривать только многоугольники, у которых любые 3 вершины не лежат на одной прямой. Такие валуны получаются из разных видов камней, необязательно однородной плотности. Тем не менее, вы знаете расположение его центра тяжести. 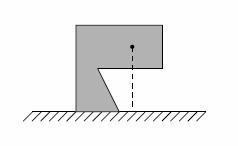Сейчас мы положили на горизонтальную прямую две вершины камня (назовём их базовыми), и отпустили. В случае, если центр тяжести находится над отрезком, соединяющим базовые вершины, или над базовыми вершинами, то валун будет стоять. Иначе сила тяжести заставит его катится в определённом направлении.

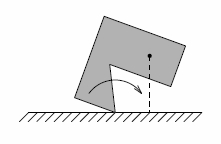
Валун будет перемещаться на одной из базовых вершин, пока он не коснётся горизонтальной прямой другой вершиной. Будем называть этот процесс поворотом. Теперь одна из базовых вершин поменялась, и возможно центр тяжести теперь находится над отрезком, соединяющим базовые вершины. В этом случае валун остановится.

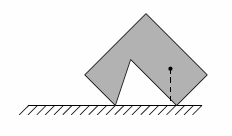
Иначе он продолжит вращаться, пока в конце концов не остановится, так как во Флатляндии вечный двигатель невозможен. Движение валуна происходит в вязкой среде, то есть инерция отсутствует, и валун остановится, как только сила тяжести позволит ему. Зная координаты вершин валуна и его центра тяжести, вычислите количество поворотов, которые совершит валун перед остановкой.

Ассоциация Великих Машин (АВМ) в последнее время совершила прорыв в археологических раскопках. Они нашли древний артефакт расписанный кодами , безусловно, созданный какой-то великой машиной много лет назад развитой ныне исчезнувшей цивилизацией. Исследователи предполагают, что эти коды скрывают знания этой цивилизации. Однако, прогресс в расшифровке кода остановился, потому что некоторые слова были сильно повреждены, а некоторые слова были непригодны для чтения.

Исследователи выяснили, что Великая Машина использовала слова только определённой структуры. Каждое слово состоит из цифр от 0 до 7 (включительно) и построено из слова "s" одним или несколькими из следующих правил:

s → 0

s → 1s

s → 2ss

s → 3sss

s → 4ssss

s → 5sssss

s → 6ssssss

s → 7sssssss

Каждое из этих правил может быть применено несколько раз, если это необходимо, и они могут быть использованы в любом порядке. Использование правила заменяет одно выбранное "s" на правую часть определённого превращения. Например, слово "2s0" может трансформироваться в "22ss0" по третьему правилу. Пожалуйста, помогите исследователям реконструировать эти слова и расшифровать все сообщения древней цивилизации. Вам предоставлен остаток правильного слова только из цифр от 0 до 7. Исследователи уверенны, что небольшая часть букв была утеряна, поэтому они хотят определить правильное слово минимальной длины, которое будет содержать данное слово как подпоследовательность.

Мальчик Кирилл написал однажды на листе бумаги строчку, состоящую из больших и маленьких латинских букв, а после этого ушел играть в футбол. Когда он вернулся, то обнаружил, что его друг Дима написал под его строкой еще одну строчку такой же длины. Дима утверждает, что свою строчку он получил циклическим сдвигом строки Кирилла направо на несколько шагов(циклический сдвиг строки abcde на 2 позиции направо даст строку deabc). Однако Дима известен тем, что может случайно ошибиться в большом количестве вычислений, поэтому Кирилл в растерянности – верить ли Диме? Помогите ему!

По данным строкам выведите минимальный возможный размер сдвига или –1, если Дима ошибся.

На одной из планет, под названием TheBestWorld, живут много умных людей. Эта планета также известна своими двумя конкурирующими школами супергероев. Каждый малыш, живущий на этой планете, мечтает стать супергероем, но не у всех это получается.

Ученики разных школ всегда недолюбливали друг друга. И иногда дело даже доходило до того, как супергерои начали применять свои геройские силы для выяснения отношений.

В этом мире случилось несчастье. На TheBestWorld нападают темные силы. У генерала главнокомандующего армией супергероев есть в распоряжении n + m супергероев, из них n — выпускники первой школы, m — второй. Главнокомандующий подсчитал количество супергероев k , которые смогут спасти лучшее, что у них есть, — планету.

На первый взгляд кажется, что главнокомандующему не понадобится помощь в выборе супергероев, но он вспомнил, что супергерои из разных школ раздражают друг друга. Но это происходит только тогда, когда два супергероя из разных школ находятся на расстоянии меньше d . Если такую пару героев позвать спасать мир, они не смогут продуктивно делать свою работу.

Проблема в том, что генерал забыл искомое d . Вам известны координаты каждого из супергероев. Генерал просит вас вычислить максимальное d , при котором он все еще может спасти мир. И выдать список супергероев, которые спасут мир при данном d .

Рассмотрим 3D модель системы координат OXYZ . Ось OX направлена направо, ось OY наверх, ось OZ от нас. В пространстве находятся прямоугольные окна. Плоскость каждого окна параллельна плоскости OXY , т.е. его стороны параллельны осям OX и OY . Все окна находятся на разной глубине (различные координаты z > 0).

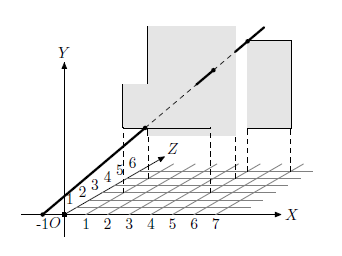
Гангстер с ружьем двигается вдоль оси OX ( y = 0, z = 0 ). Он может выстрелить пулей по прямой линии. Его цель одним выстрелом пробить все окна. Просто касания окна по ребру достаточно, чтобы оно разбилось. Ваша задача определить как совершить такой выстрел.