#112829

Ремонт дороги

Темы: [Жадный алгоритм]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2014, Задача C ]

Длина автомобильной дороги составляет N километров. Часть дороги необходимо отремонтировать. При обследовании дорога была разбита на N участков длиной 1 километр, и для каждого участка было определено, нуждается ли он в ремонте или нет, после чего был составлен план дороги, на котором отмечены участки, нуждающиеся в ремонте.

Для ремонта дороги можно привлечь несколько компаний-подрядчиков. Каждая компания может отремонтировать только непрерывный фрагмент дороги. При этом из-за требований антимонопольного законодательства длина фрагмента дороги, который ремонтирует одна компания, не должна превышать L километров (даже если на фрагменте, который ремонтирует одна компания, есть не нуждающиеся в ремонте участки, общая длина данного фрагмента не должна превышать L километров).

Определите, какое наименьшее количество компаний-подрядчиков необходимо привлечь для ремонта дороги.

Входные данные

Первая строка входных данных содержит целое число L ( L > 0 ) — максимальную длину фрагмента дороги, который может отремонтировать одна компания. Во второй строке входных данных записано целое число N ( N > 0 ) — длина всей дороги. Следующие N строк содержат по одному числу, равному 0 или 1. Число 1 обозначает, что соответствующий участок дороги нуждается в ремонте, число 0 — что участок не требует ремонта.

Выходные данные

Программа должна вывести одно целое число — минимальное количество компаний-подрядчиков, которое необходимо привлечь для ремонта дороги.

Примечание

В тесте из примера первая компания может отремонтировать участок номер 3, вторая компания — участки с 5 по 7.

Ограничения и система оценивания

Решение, правильно работающее в случае, когда числа L и N не превосходят 10, будет оцениваться в 30 баллов.

Решение, правильно работающее в случае, когда числа L и N не превосходят 1000, будет оцениваться в 60 баллов.

Решение, правильно работающее в случае, когда числа L и N не превосходят 10 ⁵ , будет оцениваться в 100 баллов.

Примеры

Входные данные

Выходные данные

#112830

Cookie Clicker

Темы: [Жадный алгоритм]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2014, Задача D ]

В игре Cookie Clicker игрок зарабатывает печеньки (cookies), щёлкая мышкой по изображению большой печеньки. Тратя заработанные печеньки, игрок может покупать различные усовершенствования (ферму, фабрику и т. д.), которые также производят дополнительные печеньки.

Рассмотрим упрощённый вариант этой игры. Пусть игрок может сделать один щелчок мышкой в секунду, что приносит ему одну печеньку. Также в любой момент времени игрок может потратить C печенек на покупку фабрики (при этом у игрока должно быть не меньше C печенек, после покупки фабрики количество его печенек моментально уменьшается на C ). Каждая купленная фабрика увеличивает ежесекундное производство печенек на P штук (то есть если у игрока одна фабрика, то он получает 1 + P печенек в секунду, две фабрики — 1 + 2 P печенек, три фабрики — 1 + 3 P печенек и т. д.). Игрок может приобрести неограниченное число фабрик стоимостью C печенек каждая. Фабрика начинает производить дополнительные печеньки сразу же, например, если после какой-то секунды игры у игрока стало C печенек, то игрок может купить фабрику и уже на следующей секунде его производство печенек увеличится на P штук.

Оригинальная игра никогда не заканчивается, но мы будем считать, что целью игры является набрать хотя бы N печенек. Определите минимальное время, за которое может быть достигнута цель игры.

Входные данные

Программа получает на вход три целых положительных числа, записанных в отдельных строках: С (стоимость фабрики), P (производительность одной фабрики) и N (необходимое количество печенек).

Выходные данные

Программа должна вывести одно целое число — минимальное время в секундах, за которое игрок может получить не менее N печенек.

Примечание

В первом тесте: через 50 секунд после начала игры у игрока будет 50 печенек, и он сможет купить фабрику. После этого он будет получать 4 печеньки в секунду, и на производство 100 печенек понадобится еще 25 секунд.

Во втором тесте: игрок сможет набрать 100 печенек за 100 секунд, при этом фабрику покупать нет смысла.

Ограничения и система оценивания

Решение, правильно работающее в случае, когда все входные числа не превосходят 1000, а для получения N печенек за минимальное время нужно приобрести не более одной фабрики, будет оцениваться в 30 баллов.

Решение, правильно работающее в случае, когда все входные числа не превосходят 1000, будет оцениваться в 70 баллов.

Решение, правильно работающее в случае, когда все входные числа не превосходят 10 ⁹ , будет оцениваться в 100 баллов.

Примеры

Входные данные

50
3
100

Выходные данные

Входные данные

99
10
100

Выходные данные

#112831

Строки

Темы: [Конструктив] [Строки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2014, Задача E ]

Даны три строки, состоящие из строчных латинских букв. С этими строками можно производить следующие операции: либо заменить один символ строки на два таких же символа (например, заменить символ «a» на «aa»), либо, наоборот, заменить два подряд идущих одинаковых символа на один такой же символ.

Необходимо при помощи этих операций сделать все три строки равными какой-то другой общей строке S либо определить, что это сделать невозможно. При этом нужно минимизировать общее количество операций.

Входные данные

Программа получает на вход три строки, состоящие из строчных букв латинского алфавита. Длина каждой строки не превышает 100 символов.

Выходные данные

Если при помощи указанных операций возможно сделать все три строки равными, выведите такую строку S , что суммарное число операций, необходимых для преобразования всех трёх данных строк к строке S , будет минимальным. Если этого сделать нельзя, программа должна вывести одно слово IMPOSSIBLE (заглавными буквами).

Примечание

Решение, которое выводит правильный ответ только на тестах из условия и тех тестах, на которых ответом является слово IMPOSSIBLE, будет оцениваться в 0 баллов.

Примеры

Входные данные

aaaza
aazzaa
azzza

Выходные данные

aazza

Входные данные

xy
xxyy
yx

Выходные данные

IMPOSSIBLE

#112902

Transformation Sequence

Темы: [Паросочетания]

Для каждой пары чисел $x$ и $y$ из диапазона $0,1,2,\ldots,N-1$ определим расстояние $D(x,y)$ как $min(|x-y|,N-|x-y|)$. Для перестановки $T$ можно построить набор чисел $D_i=D(i,T_i)$. Ваша задача состоит в обратном: по заданному набору чисел восстановить корректную перестановку, а среди таких требуется выбрать лексикографически минимальную.

Формат входных данных

В первой строке входных данных содержится число $N$ - размер перестановки. В следующей строке содержатся числа $D_0,D_1,\ldots,D_{N-1}$.

Формат выходных данных

В случае, если такой перестановки не существует, выведите «No Answer». В противном случае выведите искомую оптимальную перестановку.

Система оценки

В 30% тестовых примеров выполнено $N \le 50$
В 60% тестовых примеров выполнено $N \le 500$
В 100% тестовых примеров выполнено $N \le 10\,000$

#112910

Cheese

Темы: ["Два указателя"] [Многоугольники. Выпуклые оболочки]

Крешо купил вкуснейший сыр с перцем, но Степану перец не нравится, поэтому он хочет отрезать кусок, на котором не было бы перца. Сыр имеет форму выпуклого многоугольника, а каждая перчинка является точкой внутри него. Степан режет сыр только 1 раз. Он выбирает две вершины многоугольника, не являющиеся смежными, и режет по диагонали, соединяющей их. Затем Степан забирает ту из получившихся частей, на которой нет перца (ни внутри, ни на границе).

$\text{[math]}$

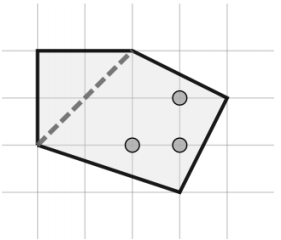
Рисунок соответствует первому тесту. Пунктирной линией показан разрез Степана.

Напишите программу, которая определит, может ли Степан отрезать кусок без перца. Если он может это сделать, выведите максимальную площадь куска, который может отрезать Степан.

Входные данные

Первая строка входного файла содержит одно целое число N — количество вершин в многоугольнике. Каждая из следующих N строк содержит два числа x _i и y _i — координаты i -й вершины. Следующая строка содержит одно число M — количество перчинок. Каждая из следующих M строк содержит два числа x _i и y _i — координаты i -й перчинки.

Вершины многоугольника заданы в порядке обхода против часовой стрелки и образуют выпуклый многоугольник. Никакие две подряд идущие стороны не параллельны.

Все перчинки расположены в различных точках и внутри многоугольника (они не расположены на стороне или снаружи многоугольника).

Выходные данные

Выведите одно число — удвоенную максимальную площадь (это число всегда целое). Если отрезать кусок без перца невозможно, выведите 0.

Примечание

Система оценки:

12 баллов. 4 ≤ N ≤ 300 , 1 ≤ M ≤ 300 .
39 баллов. 4 ≤ N ≤ 3000 , 1 ≤ M ≤ 3000 .
49 баллов. 4 ≤ N ≤ 300 000 , 1 ≤ M ≤ 300 000 .

Во всех подзадачах координаты от - 10 ⁹ до 10 ⁹ .

Примеры

Входные данные

Выходные данные