Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Во владениях короля Флатландии находится прямая дорога длиной \(n\) километров, по одну сторону от которой расположен огромный лесной массив. Король Флатландии проникся идеями защиты природы и решил превратить свой лесной массив в заповедник. Но сыновья стали сопротивляться: ведь им хотелось получить эти земли в наследство.
У короля три сына: младший, средний и старший. Король решил, что в заповедник не войдут участки лесного массива, которые он оставит сыновьям в наследство. При составлении завещания король хочет, чтобы для участков выполнялись следующие условия:
Входной файл содержит одно целое число \(n\) (\(6 \le n \le 10^9\) ).
Выходной файл должен содержать три целых положительных числа, разделенных пробелами: \(a\), \(b\) и \(c\) – длины сторон участков, которые следует выделить младшему, среднему и старшему сыну, соответственно. Если оптимальных решений несколько, разрешается вывести любое.

В этой задаче четыре подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи пройдены.
\(n \le 50\)
\(n \le 2000\)
\(n \le 40000\)
\(n \le 10^9\)
6
1 2 3
Андрей работает судьей на чемпионате по гипершашкам. В каждой игре в гипершашки участвует три игрока. По ходу игры каждый из игроков набирает некоторое положительное целое число баллов. Если после окончания игры первый игрок набрал \(a\) баллов, второй — \(b\), а третий \(c\), то говорят, что игра закончилась со счетом \(a:b:c\).
Андрей знает, что правила игры гипершашек устроены таким образом, что в результате игры баллы любых двух игроков различаются не более чем в \(k\) раз.
После матча Андрей показывает его результат, размещая три карточки с очками игроков на специальном табло. Для этого у него есть набор из n карточек, на которых написаны числа \(x_1, x_2, …, x_n\). Чтобы выяснить, насколько он готов к чемпионату, Андрей хочет понять, сколько различных вариантов счета он сможет показать на табло, используя имеющиеся карточки.
Требуется написать программу, которая по числу \(k\) и значениям чисел на карточках, которые имеются у Андрея, определяет количество различных вариантов счета, которые Андрей может показать на табло.
Первая строка входного файла содержит два целых числа: \(n\) и \(k (3 \le n \le 100 000, 1 \le k \le 10^9\) ).
Вторая строка входного файла содержит \(n\) целых чисел \(x_1, x_2, …, x_n (1 \le x_i \le 10^9 )\).
Выходной файл должен содержать одно целое число — искомое количество различных вариантов счета.
В приведенном примере Андрей сможет показать следующие варианты счета: 1:1:2, 1:2:1, 2:1:1, 1:2:2, 2:1:2, 2:2:1, 2:2:3, 2:3:2, 3:2:2. Другие тройки чисел, которые можно составить с использованием имеющихся карточек, не удовлетворяют заданному условию, что баллы любых двух игроков различаются не более чем в \(k\) = 2 раза.
В этой задаче четыре подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи пройдены.
\(3 \le n \le 100 000, k = 1, 1 \le x_i \le 100 000\)
\(3 \le n \le 100, k \le 100, 1 \le x_i \le 100\)
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\), все \(x_i\) различны
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\)
5 2 1 1 2 2 3
9
Одной из наиболее распространенных опечаток при наборе текста является перестановка двух соседних символов, например, вместо слова «программа» набрано слово «прогармма». Расстояние Левенштейна не учитывает такие опечатки: при вычислении расстояния Левенштейна одна перестановка будет считаться за два редактирования (например, удаление и вставка символа).
При вычислении расстояния Дамерау-Левенштейна, помимо операций замены, вставки и удаления символа допускается еще операция перестановки двух соседних символов. При этом между переставленными символами нельзя вставлять другие символы.
Определите расстояние Дамерау-Левенштейна для двух данных строк.
Программа получает на вход две строки, длина каждой из которых не превосходит 1000 символов, строки состоят только из заглавных латинских букв.
Требуется вывести одно число – расстояние Дамерау-Левенштейна для данных строк.
XABCDE ACBYDF
4
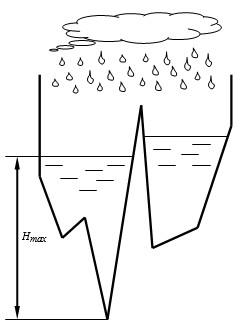
В НИИ метеорологии решили изучить процесс образования водоемов на различных рельефах местности во время дождя. Ввиду сложности реальной задачи была создана двумерная модель, в которой местность имеет только два измерения — высоту и длину. В этой модели рельеф местности можно представить как N-звенную ломаную c вершинами \((x_0, y_0), ..., (x_N, y_N)\), где \(x_0 < x_1 < ... < x_N\) и \(y_i \neq y_j\), для любых \(i \neq j\). Слева в точке \(x_0\) и справа в точке \(x_N\) рельеф ограничен вертикальными горами огромной высоты.
Если бы рельеф был горизонтальным, то после дождя вся местность покрылась бы слоем воды глубины H. Но поскольку рельеф — это ломаная, то вода стекает и скапливается в углублениях, образуя водоемы.
Требуется найти максимальную глубину в образовавшихся после дождя водоемах.
В первой строке расположены натуральное число \(N (1 \le N \le 100)\) и \(H\) — действительное число, заданное с тремя цифрами после десятичной точки \((0 \le H \le 10^9)\). В последующих \(N + 1\) строках — по два целых числа \(x_i, y_i: -10000 \le x_i, y_i \le 10000 (0 \le i \le N)\).
Числа в строках разделены пробелами.
Ответ должен содержать единственное число — искомую глубину с точностью до 4-х знаков после десятичной точки.
7 7.000 -5 10 -3 4 -1 6 1 -4 4 17 5 3 9 5 12 15
15.8446
Прямоугольная детская площадка полностью замощена \(N\) плитками. Все плитки прямоугольные, возможно разного размера. Плитки не перекрываются.
На этой площадке решили построить песочницу. Чтобы подготовить место для песочницы, необходимо вынуть не более K плиток таким образом, чтобы песочница занимала все освободившееся пространство, была прямоугольной и имела максимально возможную площадь.
Напишите программу, которая определяет расположение песочницы, удовлетворяющей перечисленным выше требованиям.
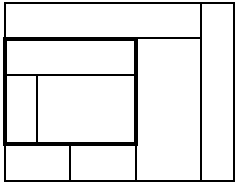
Введем систему координат так, чтобы начало координат совпадало с одним из углов площадки, а оси координат шли вдоль сторон площадки. В этом случае противоположный угол площадки окажется в точке \((X,Y)\).
Первая строка содержит два числа \(X\) и \(Y\) (натуральные числа, не превышающие 10000). Во второй строке заданы числа \(N\) и \(K (1 \le K \le N \le 2000)\). Следующие \(N\) строк файла содержат по четыре целых числа \(X_{i,1}, Y_{i,1}, X_{i,2}, Y_{i,2}\), задающих координаты двух противоположных углов плитки.
Выведите координаты двух противоположных углов найденного прямоугольника. Если решений несколько, выведите любое из них.
В этой задаче 16 тестов, каждый тест оценивается независимо.
Гарантируется, что решения, корректно работающие при \(n \le 25\) наберут не менее 30 баллов.
Гарантируется, что решения, корректно работающие при \(n \le 500\) наберут не менее 42 баллов.
Гарантируется, что решения, корректно работающие при \(n \le 1500\) наберут не менее 54 баллов.
7 5 8 3 0 0 2 1 2 0 4 1 0 1 1 3 1 1 4 3 0 3 4 4 0 4 6 5 4 0 6 4 6 0 7 5
0 1 4 4