Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 319 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 31 32 33 34 35 36 37 >> Отображать по:
#1983
На санях
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В начале XIX века еще не было самолетов, поездов и автомобилей, поэтому все междугородние зимние поездки совершались на санях. Как известно, с дорогами в России тогда было даже больше проблем, чем сейчас, а именно на N существовавших тогда городов имелась ровно N-1 дорога, каждая из которых соединяла ровно два города. К счастью, из каждого города можно было добраться в любой другой (возможно, через некоторые промежуточные города). В каждом городе имелась почтовая станция (или, как ее называют, «ям»), на которой можно было пересесть в другие сани. При этом ямщики могли долго запрягать (для каждого из городов известно время, которое ямщики в этом городе тратят на подготовку саней к поездке) и быстро ехать (также для каждого города известна скорость, с которой ездят ямщики из него). Можно считать, что количество ямщиков в каждом городе не ограничено.

Если бы олимпиада проводилась 200 лет назад, то путь участников занимал бы гораздо большее время, чем сейчас. Допустим, из каждого города в Москву выезжает участник олимпиады и хочет добраться до Москвы за наименьшее время (не обязательно по кратчайшему пути: он может заезжать в любые города,  через один и тот же город можно проезжать несколько раз). Сначала он едет на ямщике своего города. Приехав в любой город, он может либо сразу ехать дальше, либо пересесть. В первом случае он едет с той же скоростью, с какой ехал раньше. Решив сменить ямщика, он сначала ждет, пока ямщик подготовит сани, и только потом едет с ним (естественно, с той скоростью, с которой ездит этот ямщик). В пути можно делать сколько угодно пересадок.

Жюри стало интересно, какое время необходимо, чтобы все участники олимпиады доехали из своего города в Москву 200 лет назад. Все участники выезжают из своих городов одновременно.

Входные данные

В первой строке входного файла дано натуральное число N, не превышающее 2000 — количество городов, соединенных дорогами. Город с номером 1 является столицей.

Следующие N строк содержат по два целых числа: Ti и Vi — время подготовки саней в городе i, выраженное в часах, и скорость, с которой ездят ямщики из города i, в километрах в час (0 ≤ Ti ≤ 100, 1 ≤ Vi ≤ 100).

Следующие N–1 строк содержат описания дорог того времени. Каждое описание состоит из трех чисел Aj, Bj и Sj, где Aj и Bj — номера соединенных городов, а Sj — расстояние между ними в километрах (1 ≤ Aj ≤ N, 1 ≤ Bj ≤ N, Aj ≠ Bj, 1 ≤ Sj ≤ 10000). Все дороги двусторонние, то есть если из A можно проехать в B, то из B можно проехать в A. Гарантируется, что из всех городов можно добраться в столицу.

Выходные данные

Сначала выведите одно вещественное число — время в часах, в которое в Москву приедет последний участник.

Далее выведите путь участника, который приедет самым последним (если таких участников несколько, выведите путь любого из них). Выведите город, из которого этот участник выехал первоначально, и перечислите в порядке посещения те города, в которых он делал пересадки. Последовательность должна заканчиваться столицей.

При проверке ответ будет засчитан, если из трех величин «время путешествия по выведенному пути», «выведенное время» и «правильный ответ» каждые две отличаются менее чем на 0.0001.

Комментарий к примеру тестов

1. Участник из города 1 уже находится на своем месте и тратит на дорогу 0 часов. Участник из города 2 ждет 10 часов ямщика в своем городе, а затем проезжает 300 км от города 2 до города 1 за 10 часов, т.е. тратит на дорогу 20 часов. Участник из города номер 3 ждет ямщика 5 часов, а затем доезжает до города 1 за 10 часов, т.е. тратит на дорогу 15 часов. Участник из города 4 может доехать до города 1 с ямщиком из города 4 за 1 + 40 = 41 час или доехать до города номер 2 за 1 + 10 = 11 часов, прождать там 10 и доехать до столицы за 10 часов. Таким образом, он может добраться до города 1 минимум за 31 час. Это и есть самое большое время и ответ к задаче.

2. Участнику из города 2 выгоднее добраться сначала до третьего города, где ездят быстрее, а потом поехать в столицу, не делая пересадки в своём городе.

Примеры
Входные данные
4
1 1
10 30
5 40
1 10
1 2 300
1 3 400
2 4 100
Выходные данные
31.0000000000
4 2 1
Входные данные
3
1 1
0 10
0 55
1 2 100
2 3 10
Выходные данные
3.0000000000
2 3 1
#1990
Кодовый замок - 2
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной \(w\) ячеек и высотой \(h\) ячеек. В некоторых из них расположены кнопки.

Код на этом замке вводится одновременным нажатием \(k\) кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.

Для оценки надежности замков требуется написать программу для вычисления указанной величины.

Входные данные

В первой строке входного файла находятся три целых числа \(h\), \(w\) и \(k\) (\(1\le h,w\le 30\); \(1\le k \le 10\)). Каждая из последующих \(h\) строк содержит \(w\) символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.

Выходные данные

В выходной файл выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.

Примеры

Входные данные Выходные данные
2 2 2
#.
## 		2
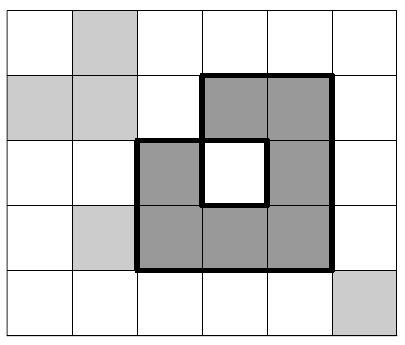
5 6 7
.#....
##.##.
..#.#.
.####.
.....# 		3

На рисунке изображен один из возможных кодов для второго примера.

#1991
Конденсация графа
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вам задан ориентированный граф с \(N\) вершинами и \(M\) ребрами (\(1\le N\le 20 000\), \(1\le M\le 200 000\)). Найдите компоненты сильной связности заданного графа и топологически отсортируйте его конденсацию.

Входные данные

Граф задан во входном файле следующим образом: первая строка содержит числа \(N\) и \(M\). Каждая из следующих \(M\) строк содержит описание ребра — два целых числа из диапазона от \(1\) до \(N\) — номера начала и конца ребра.

Выходные данные

На первой строке выведите число \(K\) — количество компонент сильной связности в заданном графе. На следующей строке выведите \(N\) чисел — для каждой вершины выведите номер компоненты сильной связности, которой принадлежит эта вершина. Компоненты сильной связности должны быть занумерованы таким образом, чтобы для любого ребра номер компоненты сильной связности его начала не превышал номера компоненты сильной связности его конца.

Примеры
Входные данные
10 19
1 4
7 8
5 10
8 9
9 6
2 6
6 2
3 8
9 2
7 2
9 7
4 5
3 6
7 3
6 7
10 8
10 1
2 9
2 7
Выходные данные
2
1 2 2 1 1 2 2 2 2 1
#1994
Форд-Беллман - 2
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
16 megabytes

В ориентированном взвешенном графе вершины пронумерованы числами от 1 до n. Если i<j, то существует ребро из вершины i в вершину j, вес которого определяется по формуле wt(i,j)=(179i+719j) mod 1000 - 500. Определите вес кратчайшего пути, ведущего из вершины 1 в вершину n.

Входные данные

Программа получает на вход одно число n (2≤n≤13000).

Выходные данные

Программа должна вывести единственное целое число - вес кратчайшего пути из вершины 1 в вершину n в описанном  графе.

Примеры
Входные данные
2
Выходные данные
117
Входные данные
3
Выходные данные
-164
#1995
Авиаперелеты
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Профессору Форду необходимо попасть на международную конференцию. Он хочет потратить на дорогу наименьшее количество денег, поэтому решил, что будет путешествовать исключительно ночными авиарейсами (чтобы не тратиться на ночевку в отелях), а днем будет осматривать достопримечательности тех городов, через которые он будет проезжать транзитом. Он внимательно изучил расписание авиаперелетов и составил набор подходящих авиарейсов, выяснив, что перелеты на выбранных направлениях совершаются каждую ночь и за одну ночь он не сможет совершить два перелета.

Теперь профессор хочет найти путь наименьшей стоимости, учитывая что до конференции осталось K ночей (то есть профессор может совершить не более K перелетов).

Входные данные

В первой строке находятся числа N (количество городов), M (количество авиарейсов), K (количество оставшихся ночей), S (номер города, в котором живет профессор), F (номер города, в котором проводится конференция).

Ограничения: 2≤N≤100, 1≤M≤105, 1≤K≤100, 1≤S≤N, 1≤F≤N.

Далее идет M строк, задающих расписание авиарейсов. i-я строка содержит три натуральных числа: Si, Fi и Pi, где Si - номер города, из которого вылетает i-й рейс, Fi - номер го-рода, в который прилетает i-й рейс, Pi - стоимость перелета i-м рейсом. 1≤Si≤N, 1≤Fi≤N, 1≤Pi≤106.

Выходные данные

Выведите одно число - минимальную стоимость пути, подходящего для профессора. Если профессор не сможет за K ночей добраться до конференции, выведите число -1.

Примеры
Входные данные
4 5 2 1 4
1 2 1
2 3 1
3 4 1
1 3 3 
1 4 5
Выходные данные
4
Страница: << 31 32 33 34 35 36 37 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест