Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 319 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 36 37 38 39 40 41 42 >> Отображать по:
#2889
Дельта, Каппа, Лямбда
  
Несколько полных подграфов соединяются между собой
#2910
Го
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Халява

Совсем недавно Али-Баба узнал от своего брата Касима об удивительной игре Го. В Го играют на прямоугольной доске – гобане, расчерченном вертикальными и горизонтальными линиями. Все линии пронумерованы. В игре участвуют два игрока, которые по очереди выставляют на гобан камни – специальные круглые фишки. Каждый камень ставится на незанятую точку пересечения линий доски (пересечения называют пунктами). У одного игрока – черные камни, у другого – белые. Камни одного цвета, смежные по вертикали, либо по горизонтали (но не диагонали), объединяются в группу. Одиночный камень также считается группой.

Один из способов набрать очки в Го – захватить камни противника. Каждый камень может иметь от двух до четырех смежных с ним пунктов (по вертикали и горизонтали, но не по диагонали). Если такой пункт не занят камнем, то он называется «дамэ». Дамэ группы – это все дамэ камней, составляющих группу. Как только оппонент своими камнями закрывает все дамэ чужой группы, то эта группа считается захваченной и снимается с доски. Если у группы осталось лишь одно дамэ, то говорят, что эта группа находится в «атари» т.е. на один шаг от захвата соперником.

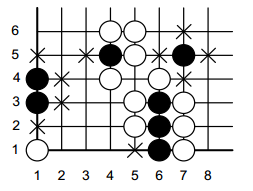
Дамэ черных камней на рисунке отмечены крестиком. Группа черных из камней (1, 3) и (1, 4) имеет 4 дамэ. Группа (6, 1), (6, 2) и (6, 3) имеет одно дамэ и находится в атари. Черный камень (4, 5) также находится в атари. Помогите Али-Бабе, который всегда играет черными, определить, какие его группы находятся в атари.

Входные данные

Описание каждого теста начинается со строки, содержащей число N – размерность игровой доски (6 ≤ N ≤ 19). Далее следует N строк по N символов каждая. Каждый символ описывает один пункт доски. «B» означает черный камень, «W» – белый, «.» означает пустой пункт. Все группы на доске имеют хотя бы одно дамэ.

Выходные данные

Выводите одно число – количество групп черных камней, находящихся в атари.

Примеры
Входные данные
9
.........
.........
.........
...WW....
...BW.B..
B..W.W...
B...WBW..
....WBW..
W....BW..
Выходные данные
2
Входные данные
6
WB.WBB
.B.W.B
..WW.W
WWW..W
..W...
BBW...
Выходные данные
1
#2911
Ковбои
  

Всем известно, что в позапрошлом веке ковбои занимались перегоном скота. Перегон скота всегда считался опасным делом. Ковбой Джон, готовясь к очередному перегону, изучал план местности. Так как местность гористая, то добраться из одного поселения в другое можно только по дорогам, возможно через другие поселения. Главной опасностью на пути были бандиты, проживающие в разных населенных пунктах, и организующие группировки для нападения на ковбоев. Чтобы их разобщить, Джон разработал гениальный план полной изоляции поселений друг от друга.

Посоветовавшись с напарниками, Джон пришел к выводу, что временно дороги можно вывести из строя, устроив камнепад. Под покровом ночи можно выехать из одного населения в другое, остановиться где-то посреди дороги и устроить камнепад так, чтобы по этой дороге нельзя больше проехать никому. Камни падают позади повозки, поэтому обратной дороги нет. Но зато можно ехать в другой населенный пункт, и если из него существуют дороги, то и их можно вывести из строя.

Сам Джон этого сделать не может, только он знает тайные тропы и должен перегонять стадо. Поэтому он решил использовать наемников. Наемники есть в любом поселении и в любом количестве, однако, за каждого из них приходится платить немалую сумму, поэтому Джон хочет потратить как можно меньше денег. Помогите Джону определить минимальное число наемников, которые смогут привести в непригодность абсолютно все дороги и изолировать все поселения.

Входные данные

В первой строке каждого теста находятся два целых неотрицательных числа N (0 < N < 1000) – количество поселений и M (0 ≤ M ≤ 100 000) – количество дорог, их соединяющих. Далее следует M строк, содержащих описание дорог. В i-й строке находятся два натуральных числа V и U (1 ≤ V, U ≤ N) – номера поселений, которые соединяет i-я дорога. Между двумя различными поселениями существует не более одной дороги, но может существовать несколько маршрутов. Нет дорог, которые образуют петлю, исходящую из поселения и ведущую в него же, не заходя в другие поселения. Не гарантируется, что существует маршрут между любой парой поселений. Маршрутом называется такая последовательность поселений s1-s2- … -sn, что любые два последовательных поселения si и si+1 соединены дорогой..

Выходные данные

Выведите минимальное количество наемников, необходимое для изоляции всех поселений.

Примеры
Входные данные
6 6
1 2
2 3
1 3
4 5
5 6
4 6
Выходные данные
2
#2914
Сусанин
  
Сложность выше среднего

Польская армия движется из Костромы в деревню Домнино. Два гетмана Стефан и Константин руководят армией. Стефан изучил карту дорог Костромской губернии и каждую ночь он ведет армию от одной деревни к некоторой другой по некоторой дороге. Константин достал карту секретных троп между деревнями и каждый день он возглавляет марш-бросок армии вдоль одной из этих троп. Каждый гетман перед маршем спрашивает дорогу у Ивана Сусанина. Таким образом, в первый день Стефан возглавляет поход, на следующий день - Константин, потом - снова Стефан и т.д.

Длина каждой дороги указана на карте Стефана. Поэтому Стефан знает минимальное расстояние от каждой деревни до Домнино, аналогично Константин знает минимальное расстояние до Домнино по своей карте. Иван Сусанин каждый раз выбирает дорогу для Стефана или тропу для Константина так, что минимальное расстояние между войском и Домнино по соответствующей карте все время строго убывает.

Помогите Ивану найти самый длинный путь в Домнино, удовлетворяющий этим условиям. Гарантируется, что Домнино достижимо из каждой деревни.

Входные данные

Первая строка входа содержит три целых числа N, S и T – количество деревень, номер начальной деревни и номер деревни Домнино (2 ≤ N ≤ 1000, 1 ≤ s, t ≤ N). Начальная точка не совпадает с Домнино.

Далее идут описание карты Стефана и карты Константина

Первая строка описания карты содержит число M – количество дорог или троп соответственно (1 ≤ M ≤ 100000). Каждая из следующих М строк содержит 3 целых числа a, b и l – описывающих дорогу/тропу между пунктами a и b с указанием длины l (1 ≤ a, b ≤ N; 1 ≤ l ≤ 106).

Выходные данные

Выведите общую длину пути (вдоль дорог и троп), который Сусанин заставит пройти польскую армию. Если он может заставить армию ходить вечно, так и не достигая Домнино, то выведите -1.

Примеры
Входные данные
5 1 5
5
1 2 2
1 4 2
2 3 1
3 4 1
5 3 1
4
1 2 2
2 4 2
2 3 1
2 5 2
Выходные данные
-1
Входные данные
3 1 3
4
1 2 10
2 3 10
1 3 20
2 3 30
4
2 1 10
1 3 10
1 1 10
2 3 10
Выходные данные
20
#2917
Киоски с мороженым
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В маленьком провинциальном городке есть маленькая школа, в которой учатся не совсем большие дети. После занятий они бегут на автобусную остановку, откуда автобус развозит их по домам.

По дороге от школы до остановки есть N перекрестков, соединенных улицами. Школьники с улицы на улицу переходят только на перекрестках.

Все школьники, как известно, любят мороженое. Известная компания Cold-N-Icy, производящая мороженое, решила воспользоваться этим. Она хочет разместить киоски с мороженым на некоторых перекрестках таким образом, чтобы любой путь школьника от школы до остановки проходил хотя бы через один перекресток, на котором установлен киоск.

Так как установка и содержание киоска — дорогое дело, то компания решила привлечь Вас для того, чтобы определить минимальное число киосков, которое необходимо установить.

Помогите компании Cold-N-Icy найти это минимальное число.

Входные данные

В первой строке входного файла находится число перекрестков N (1 ≤ N ≤ 100).

В каждой из последующих N строк находится информация о перекрестках, соединенных улицами между собой. Перекрестки нумеруются, начиная с единицы. В начале i-той строки находится число Ki – количество мест (перекрестков, школы или остановки), соединенных улицами с i-тым перекрестком. Далее идет Ki мест, разделенных пробелами. Для обозначения перекрестков используются их номера, школа обозначается как school, остановка обозначается как station.

Если перекресток i находится в списке перекрестка j, то обратное также верно.

Гарантируется, что от школы до остановки всегда существует путь.

Выходные данные

Выведите одно число — минимальное число киосков, которые планируется установить.

Примеры
Входные данные
2
2 school station
2 station school
Выходные данные
2
Страница: << 36 37 38 39 40 41 42 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест