За один шаг к числу X разрешается прибавить или из числа X разрешается вычесть любое положительное число Y, десятичная запись которого является подстрокой десятичной записи числа X. Стоимость такой операции равна сумме цифр числа Y.

Необходимо за минимальную стоимость получить из числа a число b, при этом все промежуточные числа должны быть положительными и не должны превышать n.

Джон работает на огромной парковке. Парковка представляется собой прямоугольное поле \(n \times m\), разбитое на \(n \times m\) квадратных позиций размера \(1 \times 1\). Одну из угловых позиций занимает выезд с парковки.

Машин на парковке много и вывести машину не так уж просто. Единственное, что Джон может сделать — это переместить один из автомобилей на соседнюю позицию, если она свободна. Соседними считаются позиции, имеющие общую сторону. Однако задача усложняется наличием на парковке столбов. На позиции, где стоят столбы, нельзя поставить машину. Парковка вся занята машинами и столбами и единственное свободное место — выезд с парковки. Задача Джона — вывести с парковки один из автомобилей. Помогите ему узнать, какое минимальное число действий ему придется совершить.

2390 год. В заброшенном метрополитене города N-ска завелась громадная змея-мутант. Она ползает вдоль перегонов между станциями, повергая в ужас случайно забредающих под землю потомков людей. Размеры змеи настолько велики, что иногда голова появляется на той станции, вдоль которой еще ползет какая-то другая часть тела, и змея повергает в ужас сама себя. Чтобы избавиться от этой проблемы, змея поймала вас и потребовала написать для нее программу, которая может ей прокладывать кратчайший маршрут для головы от одной станции до другой, не проползая при этом по станциям, где находятся участки ее тела.

Будем называть маршрутом последовательность станций, каждые две последовательные из которых соединены перегоном.

Все перегоны в метрополитене имеют одинаковую длину, а змея имеет длину в \((l - 0.5)\) перегонов. Змея может ползти вдоль перегонов, переползая с одного на другой на станциях. Змея может ползти вдоль перегона только в один слой, а ее голова не может появляться на станции, если в этот момент по станции проползает другая часть ее тела. Змея умеет ползать только головой вперед.

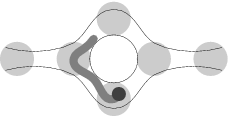
С точки зрения теории графов метрополитен города N-ска является вершинным кактусом. Это означает, что ни одна станция не лежит на двух различных циклических маршрутах и никакие два перегона не соединяют одну и ту же пару станций, никакой перегон не соединяет станцию саму с собой, от каждой станции до любой другой до появления змеи можно было добраться по перегонам.

По заданным карте метрополитена, начальному положению змеи и станции, на которую змея хочет поместить свою голову, выясните, какое минимальное количество перегонов придется проползти змее.

Отделу космических исследований поступило задание сфотографировать из космоса \(n\) объектов в заданной области. Область имеет форму квадрата размером \(50\times 50\) километров. Если разделить ее на квадраты размером \(1\times 1\) километр, то интересующие отдел объекты окажутся в центрах некоторых единичных квадратов.

Введем систему координат, направив ось OX с запада на восток и ось OY с юга на север. Тогда каждому единичному квадрату будут сопоставлены координаты в диапазоне от 1 до 50, как показано на рисунке ниже.

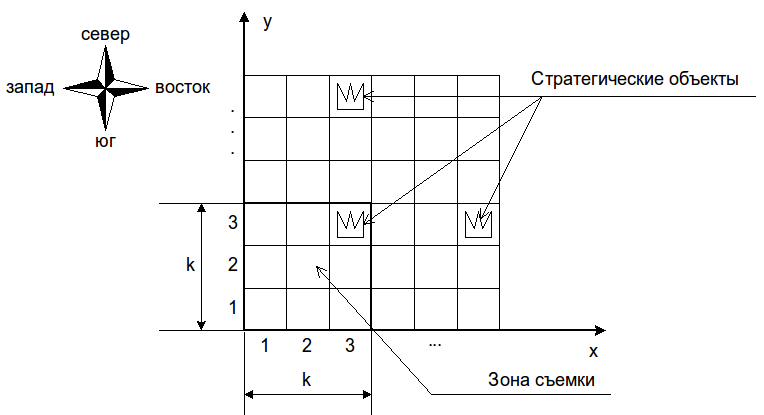
Для космической съемки используется специальный фотоаппарат высокого разрешения, установленный на космическом спутнике. Фотоаппарат может делать снимки квадратных участков земной поверхности размером \(k\times k\) километров. Исходно аппарат наведен на юго-западный угол заданной области, то есть, если сделать снимок, на нем будут видны единичные квадраты с координатами \(x\) и \(y\) от \(1\) до \(k\) километров.

С помощью специальных двигателей можно изменять орбиту спутника, что приводит к изменению участка съемки. За один день орбиту спутника можно изменить таким образом, что участок съемки сместится либо на один километр на запад, либо на один километр на восток, либо на один километр на север. Переместить участок съемки на юг невозможно. Непосредственно между перемещениями спутника можно сделать снимок, временем съемки можно пренебречь.

Руководство отдела заинтересовалось вопросом: за какое минимальное количество дней можно сделать снимки всех объектов заданной области.

Требуется написать программу, которая по заданному расположению объектов и размеру снимка \(k\) определит минимальное время, за которое можно сделать снимки всех объектов заданной области.