Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
Однажды в далекой-далекой стране правительство создало Министерство по сокращению бумажной волокиты. Как вы наверное догадались, это было крупнейшее министерство за всю историю страны. Количество сотрудников было поистине огромным. Несмотря на это, структура министерства была очень простой: каждый сотрудник имел не более трёх подчинённых, каждый из которых снова имел не более трех подчиненных и так далее...
В результате последних выборов был избран новый министр. Он был молод, умён и непорочен, и сразу же решил оправдать название своего учреждения. Он заметил, что многие части иерархической структуры совпадают, и решил, что должны совпадать и их обязанности. А если две структуры делают одно и тоже, одна из них является лишней, и ее работники должны быть уволены. Ваша задача найти количество различных департаментов и вывести результат в необходимом формате.
Вам дана структура министерства. Каждый работник имеет одного начальника и не более трёх подчинённых(возможно ноль). Единственным исключением является министр — у него нет начальника(но так же не более трех подчинённых). Конечно нет определённого порядка, в котором перечисляются подчинённые. Департамент состоит из должностного лица, всех его подчинённых и их подчинённых, и т.д.
Есть два особых случая:
Высотой департамента назовем длину максимальной последовательность сотрудников x 1 , ..., x d такую, что сотрудник x i является начальником сотрудника x i + 1 для всех 1 ≤ i < d . Заметим что высота департамента, состоящего из одного сотрудника равна 1 .
Два департамента A и B совпадают, если существует взаимно-однозначное отображение, сопоставляющее каждому сотруднику x A из департамента A сотрудника x B из департамента B , таким образом, что сотрудник x A является начальником сотрудником y A , тогда и только тогда, когда x B является начальником y B . Заметим, что если два департамента совпадают, то они имеют одинаковую высоту, одинаковое количество сотрудников и начальнику первого департамента соответствует начальник второго.
На приведенных картинках департаменты A и B совпадают, а C не совпадает ни с A , ни c B .
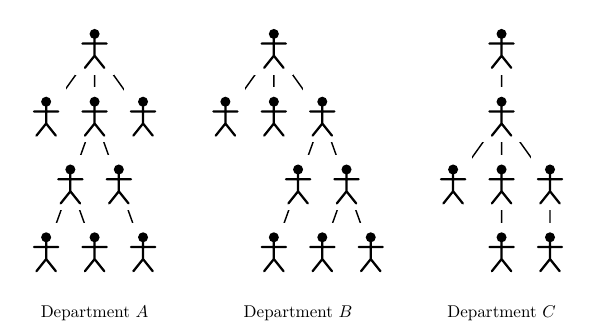
Вам необходимо для каждой высоты вычислить количество различных департаментов имеющих такую глубину. Формально требуется построить последовательность n 1 , ..., n d , где d это высота всего министерства, а n i — количество различных департаментов высоты i .
Входной файл содержит единственную строку, которая описывает иерархическую структуру министерства, используя следующую нотацию. Каждый департамент кодируются строкой "( x 1 ... x k )", где k — количество подчинённых у начальника департамента, а строки x i — коды им подчиняющихся департаментов. Департамент, состоящий из одного человека, кодируется строкой "()". Структура министерства задается кодом всего министерства. Количество сотрудников министерства не превосходит 1 000 000 (включая министра).
Выходной файл должен содержать d строк, где d это высота министерства. i -ая строка должна содержать количество различных департаментов высоты i .
Приведенная картинка иллюстрирует пример из условия.
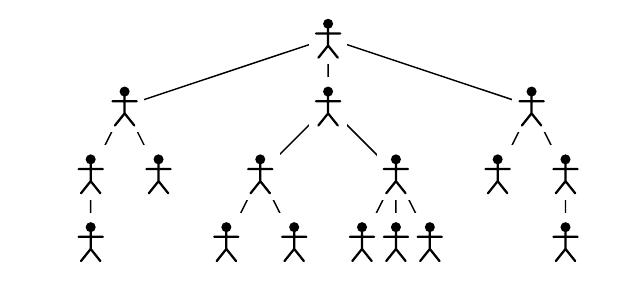
(((())())((()())(()()()))(()(())))
1 3 2 1
В секретном 240 отделе ИПФ РАН \(N\) сотрудников и \(N\) компьютеров. В отделе вводятся новые требования к секретности. В соответствии с этими требованиями, для каждого сотрудника будут определены ровно \(K\) компьютеров, к которым этот сотрудник будет иметь допуск (т.е. за которыми этот сотрудник будет иметь право работать), причём так, что к каждому компьютеру будут иметь допуск ровно \(K\) сотрудников.
Информация о том, какой сотрудник к какому компьютеру будет иметь допуск, будет известна лишь непосредственно перед вступлением новых требований в силу. Таким образом, чтобы не прерывать работу отдела, сотрудники должны будут быстро решить, кто за каким компьютером будет работать. Для этого им необходимо заранее написать программу, которая по любому распределению допусков сотрудников найдёт рассадку сотрудников по компьютерам, удовлетворяющую этим допускам.
Обратите внимание, что значение \(K\) тоже будет известно лишь в последний момент. Из общих соображений секретности известно лишь, что \(K\) будет равняться или 1, или 2, или 4; поэтому ваша программа должна уметь работать для любого из этих трех значений \(K\).
В первой строке входного файла записаны натуральные числа \(N\) и \(K\) (\(1\leq N \leq 100 000\)). Далее следуют \(KN\) строк, в каждой из которых записаны два натуральных числа — номер сотрудника и номер компьютера, к которому этот сотрудник имеет допуск.
Гарантируется, что каждый сотрудник имеет допуск ровно к \(K\) компьютерам, что к каждому компьютеру ровно \(K\) сотрудников имеют допуск, и что \(K\) равно либо 1, либо 2, либо 4.
В выходной файл выведите \(N\) строк, в каждой по два числа — номер сотрудника и номер компьютера, за которым он должен работать. Строки можно выводить в произвольном порядке.
Если есть несколько решений, выведите любое. Можно доказать, что для любого входного файла, удовлетворяющего указанным ограничениям, всегда имеется как минимум одно решение.
| Ввод | Вывод |
|---|---|
3 1 2 3 3 1 1 2 |
3 1 1 2 2 3 |
2 2 1 2 2 1 2 2 1 1 |
1 2 2 1 |
НЛО приземлилось в районе реки, ее вид заворожил инопланетян, потому что на их планете вообще нет рек. Сейчас они хотят построить свой инопланетный поселок на одной из земных рек, но также они знают, что на Земле очень хрупкая экосистема, поэтому нельзя перегораживать реку очень сильно. Но инопланетяне абсолютно не знают, как устроены реки, поэтому они обратились к вам с просьбой написать программу, которая вычислит максимальную пропускную способность реки, после постройки их инопланетного поселка.
Инопланетяне предпочитают строить здания на тех реках, берега которых представляют из себя параллельные прямые, поэтому область реки, где будут строить инопланетяне, можно себе представить как прямоугольную таблицу W × H , у которой каждая клеточка имеет координаты ( X , Y ). Каждая клеточка пропускает через себя 1 кубический метр воды в секунду, и вода может перетекать только между клеточками соседним по стороне. Каждая клеточка на южной стороне реки ( Y = 0 ) имеет приток воды из реки в размере 1 кубический метр воды в секунду. Каждый дом в поселке занимает прямоугольник, состоящий из единичных клеточек; если в клеточке стоит дом, то вода через нее протекать не может. Ваша задача — вычислить, сколько кубических метров за секунду пропускает поселок инопланетян. То есть сколько кубических метров воды вытекает из всех северных клеток поселка ( Y = H - 1 ) в сумме.
Как известно, вода несжимаема, то есть не может накапливаться в клетке, соответственно если в клетку втекло сколько-то воды, то столько же должно и вытечь.
В первой строке содержатся два целых числа W и H — ширина и высота реки соответственно (\(3\leq W \leq 1000;\; 3\leq H \leq 10^{8})\). В следующей строке находится число B — количество домов в поселке инопланетян (\(0 \leq B \leq 1000\)).
Следующие B строк содержат четыре целых координаты X 0 , Y 0 , X 1 , Y 1 . Где X 0 и Y 0 — координаты нижней левой клеточки дома, а X 1 и Y 1 — координаты верхней правой клеточки дома ( 0 ≤ X 0 ≤ X 1 < W и 0 ≤ Y 0 ≤ Y 1 < H ). Домики не перекрываются, но могут касаться по стороне или ребрам.
Выведите одно число — максимальную пропускную способность поселка в кубических метрах в секунду.


3 3 2 2 0 2 0 0 2 0 2
1
5 6 4 1 0 1 0 3 1 3 3 0 2 1 3 1 5 2 5
2
Островное государство Исола состоит из n островов. Для удобства передвижения между некоторыми островами были построены мосты, но чтобы никакой остров не был перегружен транспортом, к каждому острову ведет не более двух мостов. По мосту можно проезжать в обоих направлениях. Для получения средств на поддержание мостов и дорог правительство Исолы установила плату за проезд по мосту в размере одной условной единицы.
До недавнего времени в Исоле не было автобусного сообщения. В срочном порядке была основана первая автобусная компания «Коррейра», и решено проложить по автобусному маршруту между каждой парой островов. Поскольку между некоторыми островами не существует пути по мостам, между такими островами решено маршрут не создавать.
Было решено, что каждому маршруту будет совершаться два рейса в сутки: сначала в одном направлении, а затем в обратном. Естественно автобусы всегда движутся по самому дешевому маршруту. В «Коррейре» очень интересуются, сколько условных единиц в день будет уходить на оплату проездов автобусов по мостам. Поскольку программистов в небольшом государстве Исолы нет, компания просит Вас решить эту задачу.
В первой строке два целых числа n и m ( 1 ≤ n ≤ 100000 ; 0 ≤ m ≤ n ) — количество островов и мостов Исолы. Далее следует m строк, описывающих мосты Исолы. В каждой строке содержится два целых числа x и y ( 1 ≤ x , y ≤ n ; x ≠ y ) — номера островов, соединенных мостом. Гарантируется что к каждому острову ведет не более двух мостов.
В выходной файл выведите единственное целое число — количество условных единиц, необходимых для работы автобусного сообщения.
В первом примере не все острова соединены между собой. От первого острова до второго можно добраться по одному мосту, от первого до третьего — один мост, от второго до третьего — один. До четвертого или пятого от первого, второго или третьего островов добраться по мостам нельзя. От четвертого до пятого — один мост. Итого 2(1 + 1 + 1 + 1) = 8 условных единиц.
5 4 1 2 1 3 2 3 5 4
8
5 4 5 4 4 3 3 2 2 1
40
В стране Байтландии есть n городов, соединенных дорогами. Каждая дорога двухсторонняя и имеет некоторую длину. Также, в стране есть две партии — одна выступает за то, что вилку необходимо держать во время еды в левой руке, другая — за то, что вилку необходимо держать в правой руке. В каждый момент времени каждый из городов поддерживает только одну партию. Вот только время от времени в городах происходят перевороты и в одном из городов поддерживаемая партия меняется на противоположную.
Правительство Байтландии поручило Вам написать программу, которая бы в каждый момент времени оценивала стабильность политической ситуации в стране. Согласно математической модели, разработанной ведущими учеными Байтландии, стабильность зависит от того, насколько близко находятся города, поддерживающие одну и ту же партию, поскольку чем ближе они, чем больше вероятность того, что они могут объединиться в коалицию.
Поэтому программа, написанная Вами, должна по информации о всех городах, дорогах и происходящих переворотах находить, после каждого переворота, два города, поддерживающих одну партию, и находящихся на наименьшем расстоянии друг от друга.
Первая строка входного файла содержит три целых числа n, m и k (1 ≤ n, m, k ≤ 100000) — количество городов, дорог и переворотов соответственно.
Вторая строка содержит строку s длиной n, описывающую политическую ситуацию в стране на момент начала наблюдения. Символ L на i-ой позиции означает, что город номер i поддерживает партию, выступающую за то, что вилку необходимо держать в левой руке, символ R — в правой.
Следующие m строк содержат по три целых числа ai, bi и li (1 ≤ ai, bi ≤ n, ai ≠ bi, 1 ≤ li ≤ 109) — номера городов, которые соединены i-ой дорогой и ее длина. Каждая пара городов соединена не более, чем одной дорогой.
В последней строке содержится k чисел --- номера городов cj (1 ≤ cj ≤ n), в которых происходили перевороты в порядке их происшествия. Поскольку все города достаточно консервативны, то в каждом городе произошло не более одного переворота, то есть все cj различны.
В выходной файл выведите k + 1 отчет о ближайших городах, которые могут объединиться в коалицию. Первое описание должно соответствовать началу наблюдения, каждое следующее — после очередного переворота в одном из городов.
Каждое описание должно быть выведено на отдельной строке и содержать три целых числа di, xi и yi — минимальное расстояния между городами, поддерживающими одну партию и номера этих городов, соответственно. Если таких пар несколько, выведите любую. Гарантируется, что хотя бы одна такая пара всегда существует.
n ≤ 100. Решение оценивается в 30 баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в 40 баллов.
5 6 4 LRLRL 1 4 1 2 3 2 3 4 3 4 5 4 2 5 5 2 4 6 1 4 3 5
4 1 3 1 1 4 3 3 4 2 2 3 2 2 3