Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
Вася открыл для себя классическую игру «Bomberman», действующий лицом которой является Бомбермен. Этот персонаж передвигается по игровому полю, представляющему собой прямоугольник из N строк и M столбцов. Каждая клетка поля либо свободна для прохода, либо занята стеной. В одной из клеток находится бонус, к которому необходимо добраться Бомбермену. Для этого у него есть ровно 3 бомбы. За ход Бомбермен может сдвинуться в соседнюю клетку, если она свободна, или взорвать стену, расположенную в ней, использовав одну бомбу.
В последнем случае клетка становится проходимой и впоследствии Бомбермен может на нее встать. Вася хочет определить, за какое минимальное количество ходов Бомбермен сможет добраться до бонуса, или же узнать, что это сделать невозможно, тогда Вася может спокойно удалить «Bomberman» - а и вернуться к старой доброй Дотке.Соседними являются клетки, имеющие общую сторону. Бомбермен не может выходить за границы поля.
В первой строке содержатся два числа N и M — количество строк и столбцов поля соответственно ( 1 ≤ N , M ≤ 20 ). Каждая из следующих N строк содержит ровно M символов, описывающих поле. Свободные клетки обозначены символом «.» (ASCII код 46), занятые—символом «W» (ASCII код 87), бонус—символом «*» (ASCII код 42), Бомбермен—символом «B» (ASCII код 66). Гарантируется, что на поле находится ровно один бонус.
Выведите одно число—минимальное количество ходов, необходимое для того, чтобы добраться до бонуса, либо −1, если добраться до бонуса невозможно.
В первом примере необходимо взорвать стену во второй строке в первом столбце и пройти Бомберменом вниз, а затем вправо. Во втором примере необходимо взорвать минимум 4 стены, чтобы добраться до бонуса, поэтому ответ −1.
5 6 B..... WWWWW. ...... .WWWWW .....*
10
9 12 WWWWWWWWWWWW WW...B..WWWW WW.WWWW.WWWW WW.WWWW...WW WW.WWWWWWWWW WWWWWWWWWWWW WWWWWWWWWWWW WWWW*WWWWWWW WWWWWWWWWWWW
-1
Петар организует вечеринку по случаю своего дня рождения и планирует пригласить некоторых сотрудников из компании, где он работает генеральным директором. Каждый сотрудник, включая Петара, имеет уникальный номер от 1 до N и тип шуток, которые он рассказывает, V i . Также, каждый сотрудник в компании кроме Петара имеет ровно одного начальника. Так как Петар - генеральный директор компании, он имеет номер 1 и руководит всеми сотрудниками (не обязательно напрямую).
На вечеринке есть некоторые правила, которым должны отвечать все присутствующие: 1. На вечеринке не должно быть двух людей с одинаковым типом шуток. 2. Человек не может быть приглашен на вечеринку, если на нее не приглашен его прямой начальник. 3. Человек не может быть приглашен на вечеринку, если типы шуток, которые рассказывает он и его приглашенные подчиненные, не образуют последовательное множество.
Петар хочет знать, сколько возможных наборов типов шуток может быть на его вечеринке, если он пригласит людей в соответствии с вышеуказанными правилами.
Последовательное множество - такое множество, в котором, если отсортировать его по возрастанию, разность между соседними элементами будет равна 1. Например (3, 1, 2) и (5, 1, 2, 4, 3) - последовательные множества, а (2, 5, 3) - нет.
Первая строка содержит одно целое число N ( 1 ≤ N ≤ 10000 ). Вторая строка содержит N целых чисел V i - типы шуток, рассказываемые i -м человеком ( 1 ≤ V i ≤ 100 ). Каждая из следующих N - 1 строк содержит два целых числа A и B ( 1 ≤ A , B ≤ N ), обозначающих что сотрудник с номером A является прямым начальником сотрудника с номером B .
Выведите единственное число - количество возможных наборов типов шуток на вечеринке.
4 2 1 3 4 1 2 1 3 3 4
6
4 3 4 5 6 1 2 1 3 2 4
3
6 5 3 6 4 2 1 1 2 1 3 1 4 2 5 5 6
10
Путешествие по стране никогда не бывает простым, особенно когда не существует прямого сообщения между городами. Группа туристов хочет добраться в город Метрополис, используя сеть железных дорог, которая соединяет n городов, пронумерованных от 1 до n. Город, из которого выезжает группа, имеет номер 1, Метрополис имеет номер n.
На железной дороге постоянно функционируют m маршрутов поездов. Каждый маршрут определяется последовательностью городов, перечисленных в том порядке, в каком их проезжает поезд, обслуживающий этот маршрут. В каждом маршруте для каждой пары соседних городов задано время, за которое поезд этого маршрута проезжает перегон между этими городами. При этом поезда разных маршрутов могут проезжать один и тот же перегон за разное время.
По пути в Метрополис группа может садиться на поезд и сходить с поезда в любом городе маршрута, не обязательно в начальном или конечном. При этом, можно сойти с поезда маршрута i, пересесть на поезд маршрута j, возможно сделать еще несколько пересадок, а потом вновь сесть в поезд того же маршрута i.
Туристы предъявляют высокие требования к выбору способа проезда в Метрополис.
Во-первых, суммарное время, проведенное в поездах, должно быть минимальным.
Во-вторых, среди всех способов с минимальным временем нахождения в поездах предпочтительным является тот способ, для которого сумма квадратов промежутков времени, непрерывно проведенных в поезде между двумя пересадками, максимальна. Назовём эту сумму качеством путешествия.
Время, проведенное вне поездов, не учитывается.
Требуется написать программу, которая по описаниям имеющихся маршрутов поездов определит минимальное время, которое группе туристов придется провести в поездах, а также максимальное качество путешествия с таким временем.
В первой строке входных данных заданы два целых числа (2 ≤ n ≤ 106, 1 ≤ m ≤ 106) — количество городов и количество маршрутов соответственно.
Далее в m строках содержится описание маршрутов.
Описание каждого маршрута начинается с целого числа si — количество перегонов в маршруте с номером i (1 ≤ si ≤ 106). Далее следуют (2si + 1) целых чисел, описывающих города маршрута и время проезда перегона между соседними городами маршрута, в следующем порядке: vi, 1, ti, 1, vi, 2, ti, 2, vi, 3, ..., ti, si, vi, si + 1, где vi, j — номер j-го города маршрута, ti, j — время проезда перегона между j-м и (j + 1)-м городом (1 ≤ vi, j ≤ n, 1 ≤ ti, j ≤ 1000).
Гарантируется, что s1 + s2 + ... + sm ≤ 106. Никакие два города в описании маршрута не совпадают. Гарантируется, что с помощью имеющихся маршрутов можно добраться из города с номером 1 в город с номером n.
Выходные данные должны содержать два целых числа — минимальное суммарное время, которое придется провести в поездах, и максимальное качество пути с таким временем.
В первом примере группа туристов отправится прямым маршрутом в Метрополис.
Во втором примере не оптимально проехать напрямую по первому маршруту, так как время в поезде при этом не будет минимальным возможным. Поэтому они отправятся на поезде по маршруту 1 из города 1 в город 2, затем на поезде по маршруту 2 из города 2 в город 3, а затем снова на поезде по маршруту 1 из города 3 в город 5. При этом сумма квадратов промежутков времени, проведенных в поездах между пересадками, равна 32 + 12 + 52 = 35.
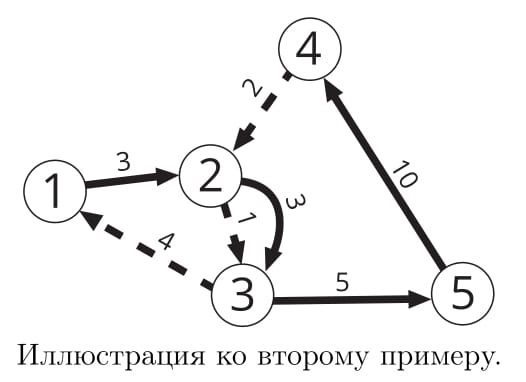
В третьем примере добраться из города 1 в город 4 за минимальное время можно, пересаживаясь с маршрута 1 на маршрут 2 в любом из городов 2, 3 или 4. Максимальное качество путешествия достигается при пересадке в городе 2: 12 + 92 = 82.
Обратите внимание, что второй и третий примеры не удовлетворяют ограничениям первой и второй подзадачи, решение будет протестировано на этих подзадачах, если оно пройдет первый тест из примера. Все тесты из примера подходят под ограничения подзадач 3 – 7, решение будет проверяться на тестах этих подзадач только в случае прохождения всех тестов из примера.

2 1 1 1 3 2
3 9
5 2 4 1 3 2 3 3 5 5 10 4 3 4 2 2 1 3 4 1
9 35
5 2 3 1 1 2 2 3 3 4 3 2 2 3 3 4 4 5
10 82
Вы наверняка слышали легенду о Короле Артуре и Рыцарях Круглого Стола. Практически все версии этой истории указывают на то, что круглость Круглого Стола тесно связана с верой Артура в равенство среди рыцарей. Это ложь! На самом деле выбор Артура касательно формы стола вызван его детской травмой.
В реальности Артур был принужден убирать и мыть квадратные столы с юного возраста после того как на них играли в бирюльки. После соревнований по этой игре обычно на столе остается множество палочек, не касающихся друг друга. В духе соревнования, организаторы установили свод строгих правил для уборщиков. Точнее, палочки со стола должны быть убраны одна за другой путем их сдвига к ближайшему к уборщику краю стола. Они не должны вращаться и касаться других палочек в процессе перемещения.
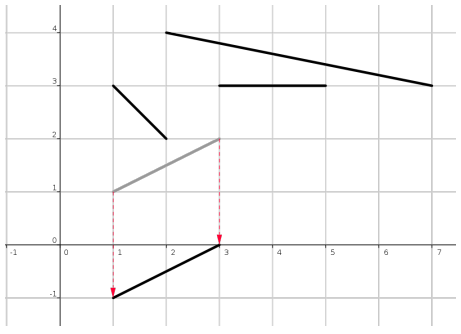
В этой задаче представим стол на координатной плоскости как квадрат с противоположными вершинами в точках (0, 0) и (10000, 10000), где палочкам соответствуют прямые отрезки, лежащие внутри квадрата. Предположим, что Артур сидит у края стола, прилежащего к оси X. Тогда уборка палочек со стола сводится к передвижению их к оси X, покуда они не упадут со стола. Ваша задача - определить порядок уборки палочек со стола, который соответствует условиям из предыдущего абзаца.
Первая строка содержит единственное целое число N ( 1 ≤ N ≤ 5000 ) - количество палочек на столе. Каждая из следующих N строк содержит 4 целых числа x 1 , y 1 , x 2 , y 2 ( 0 ≤ x 1 , y 1 , x 2 , y 2 ≤ 10000 ), обозначающих крайние точки палочек.
В единственной строке выведите N целых чисел - номера палочек в том порядке, в котором они должны быть убраны со стола. Если существует несколько решений, выведите любое из них.
4 1 3 2 2 1 1 3 2 2 4 7 3 3 3 5 3
2 4 1 3
4 0 0 1 1 1 2 0 3 2 2 3 3 4 0 3 1
4 3 1 2
3 4 6 5 5 2 1 15 1 3 2 8 7
2 3 1
Ученые в тайной химической лаборатории в Хорватии изучают химические связи в недавно обнаруженном веществе инопланетного происхождения. Имеющаяся в распоряжении ученых порция вещества состоит из N молекул, соединенных между собой N - 1 ковалентными связями, и все молекулы объединены этими связями (не обязательно напрямую) в единую сеть.
Так как вещество нестабильное, в каждой молекуле регулярно возникают импульсы, перемещающиеся по веществу через существующие связи в обоих направлениях. Ученые собираются стабилизировать вещество, направив ковалентные связи (то есть, дав импульсам возможность путешествовать по ним между молекулами лишь в одном направлении). Показатель нестабильности вещества определяется длиной максимального пути, который может пройти импульс в нем, и ученые хотят сделать эту величину как можно меньше.
Помогите ученым создать вещество с минимальным показателем нестабильности, указав необходимое направление ковалентных связей.
Первая строка содержит одно целое число N ( 2 ≤ N ≤ 100000 ). Каждая из последующих N - 1 строк содержит по два целых числа a i и b i ( 1 ≤ a i , b i ≤ N ), которые показывают что молекулы с номерами a i и b i соединены ковалентной связью.
Выведите N - 1 строку, каждая из которых должна содержать 1 если ковалентная связь должна быть направлена от a i к b i или 0 в противном случае.
Решения, в которых N ≤ 20 , будут оцениваться в 30 баллов.
3 1 2 2 3
0 1
4 2 1 1 3 4 1
1 0 1