Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
В Флатландии идет пора реформ. Недавно была проведена реформа дорог, так что теперь по дорогам страны из любого города можно добраться в любой другой, причем только одним способом. Также была проведена реформа волшебников, так что в каждом городе остался ровно один волшебник. Теперь же началась реформа почтовой системы.
Недавно образованное почтовое агентство «Экс-Федя» предлагает уникальную услугу — коллективную посылку. Эта услуга позволяет отправлять посылки жителям всех городов на каком-либо пути по цене обычной посылки. Удивительно, но пользоваться такой услугой стали только волшебники Флатландии, которые стали в большом количестве отправлять друг другу магические кактусы. Агентство столкнулось с непредвиденной проблемой: как известно, все волшебники живут в башнях и мало того, что не строят в них лестницы, так еще время от времени меняют их высоту. Поэтому, чтобы доставить посылку волшебнику, который живет в башне высотой h , курьеру агентства требуется иметь с собой не менее h метров веревки.
Вам поручено руководить отделом логистики — по имеющимся данным о высотах башен и об их изменениях вам нужно определять минимальную длину веревки, которую нужно выдать курьеру, который доставляет посылки между городами i и j .
Первая строка входного файла содержит число n — количество городов в Флатландии ( 1 ≤ n ≤ 50 000 ). Во второй строке находится n положительных чисел, не превосходящих 10 5 — высоты башен в городах. В следующих n - 1 строках содержится по два числа u i и v i — описание i -й дороги, 1 ≤ u i , v i ≤ n , u i ≠ v i . В следующий строке содержится число k — количество запросов ( 1 ≤ k ≤ 100 000 ). В следующих k строках содержатся описания запросов в следующем формате:
Для каждого запроса доставки посылок выведите минимальную длину веревки, которую необходимо выдать курьеру.
20 баллов — ( 1 ≤ n, k ≤ 100) .
30 баллов — каждый город соединен дорогами не более чем с двумя другими.
50 баллов — полные ограничения.
3 1 2 3 1 3 2 3 5 ? 1 2 ! 1 5 ? 2 3 ! 3 2 ? 1 2
3 3 5
1 100 5 ! 1 1 ? 1 1 ! 1 1000 ? 1 1 ! 1 1
1 1000
Рассмотрим следующую игру об удалении вершин из графа, представляющего лес (то есть объединение нескольких деревьев). Изначально граф состоит из одного дерева из n вершин, а количество очков равно 0 .
Игра задаётся перестановкой вершин и происходит следующим образом:
Просуммируем число очков по всем возможным n ! играм. Выведите это число по модулю 10 9 + 7 .
В первой строке входного файла дано число N ( 2 ≤ n ≤ 10 5 ) — количество вершин в исходном дереве.
Каждая из последующих N - 1 строк содержит два числа — x i , y i задающих концы соответствующего ребра дерева ( 1 ≤ x i , y i ≤ n ).
Выведите одно число — суммарное количество очков по модулю 10 9 + 7 .
Тесты к данной задаче состоят из 3 групп:
2 1 2
6
3 1 2 2 3
34
Ивица — страстный компьютерщик. Недавно он начал работать над своей первой компьютерной игрой — клоном популярного тетриса. Хотя игра далека от завершения, его программа уже поддерживает размещение в матрице N × M пяти разных фигур Тетриса (показанных на изображении ниже) в матрице. Перед тем, как поместить фигуру в матрицу, её можно поворачивать на 90 градусов произвольное число раз и можно окрашивать. Кроме того, текущая версия игры не поддерживает размещение фигуры, если она при этом выходит за границы матрицы или перекрывается с другими существующими фигурами в матрице.

Пока Ивица учился в школе, его сестра Марика начала игру и случайным образом повернула, покрасила и поместила фигуры, но таким образом, что соседние фигуры окрашены по-разному. Две фигуры смежны, если они имеют общую сторону или общий угол.
Он хочет знать для каждого из пяти типов фигуры, сколько таких фигур его сестра разместила в матрицу, пока он занят улучшением игры.
Первая строка ввода содержит положительные целые числа N и M ( 1 ≤ N , M ≤ 10 ), которые представляют количество строк и столбцов матрицы Тетриса. Каждая из следующих N строк содержит M символов, которые представляют матрицу. Каждый символ может быть « . », что означает пустую клетку или строчной буквой английского алфавита, которая представляет часть фигуры. Различные буквы представляют разные цвета, а клетки одной фигуры имеют одинаковый цвет.
Гарантируется, что вводная матрица могла быть получена последовательным добавлением фигур Тетриса в изначально пустую матрицу.
Вы должны вывести ровно пять строк. i -я строка должна содержать количество фигур i -го типа, находящихся в данной матрице.

4 5 aaaa. .bb.. .bbxx ...xx
2 1 0 0 0
4 5 .aab. aabb. .cbaa cccaa
1 0 1 1 1
5 7 .c..... ccdddd. caabbcc aabbacc ...aaa.
1 1 2 1 1
Мирко стал генеральным директором крупной корпорации. В компании работает N человек, пронумерованных от 1 до N , Мирко имеет номер 1 . У всех кроме Мирко есть начальник. Начальник может иметь несколько подчинённых, но не более одного своего начальника.
Когда Мирко получает задание от инвесторов, он передаёт его своему подчинённому с наименьшим номером. Этот подчинённый также передаёт его своему подчинённому с наименьшим номером, и так далее, пока задание не перейдёт несчастливому работнику без подчинённых, который должен сделать задание.
Этот работник получает 1 монету, его начальник получает 2 монеты, начальник этого начальника получает 3 и так далее. Потом тот, кто на самом деле сделал работу, осознаёт, насколько эта капиталистическая система несправедлива и увольняется с работы.
Мирко получает задания до тех пор, пока в корпорации не останется всего один сотрудник — сам Мирко. Тогда он выполняет это задание, получает 1 монету и уходит из корпорации. Ему стало интересно, сколько всего монет получил каждый бывший сотрудник. Помогите ему с этим.
Первая строка содержит одно натуральное число N ( 1 ≤ N ≤ 2·10 5 ) — число сотрудников компании. Следующая строка содержит N - 1 чисел a 2 , a 3 , ... a n ( 1 ≤ a i < i ), a i — номер начальника i -го сотрудника.
Выведите N чисел, i -е число должно означать, сколько монет получил i -й сотрудник
Программы, верно работающие при 2 ≤ N ≤ 5000 оцениваются в 50 баллов.
Пояснения к первому примеру:
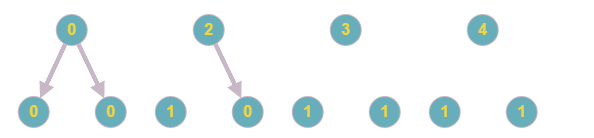
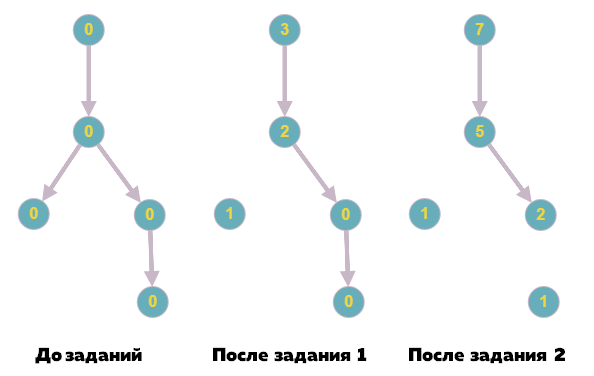
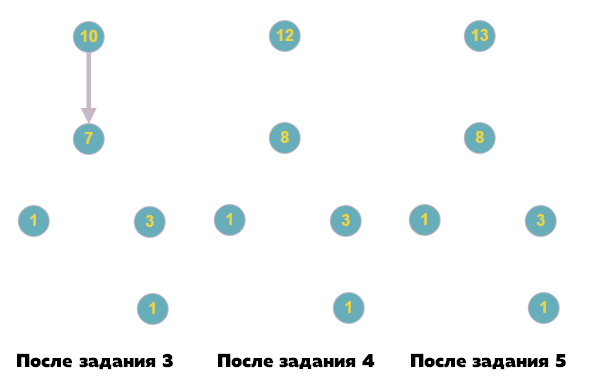
3 1 1
5 1 1
5 1 2 2 4
13 8 1 3 1
Петя увлёкся алгоритмами сжатия данных. Он уже изучил форматы gz , bz , zip и несколько других. Воодушевившись новыми знаниями, Петя собрался разработать свой формат сжатия и назвать его dis .
Петя решил сжимать таблицы. У него есть таблица, состоящая из n строк и m столбцов, заполненная целыми положительными числами. Он хочет заменить значения элементов таблицы на целые положительные числа так, чтобы отношение элементов в каждой строке и каждом столбце не изменилось. То есть, если в некоторой строке исходной таблицы a i , j < a i , k , то и в сжатой таблице a ' i , j < a ' i , k , и если a i , j = a i , k , то a ' i , j = a ' i , k . Аналогично, если в некотором столбце исходной таблицы a i , j < a p , j , то и в сжатой таблице a ' i , j < a ' p , j , и если a i , j = a p , j , то a ' i , j = a ' p , j .
Поскольку б'{о}льшие значения требуют больше места для хранения, максимальное значение элемента получившейся матрицы должно быть как можно меньше.
В теории Петя мастер, но вот писать код он не любит. Помогите ему реализовать формат сжатия dis .
В первой строке входных данных содержатся два числа
n
и
m
(
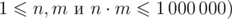 — количество строк и столбцов таблицы соответственно.
— количество строк и столбцов таблицы соответственно.
В следующих n строках содержится по m целых чисел a i , j (1 ≤ a i , j ≤ 10 9 ) — значения элементов таблицы.
Выведите сжатую таблицу: n строк, содержащих по m чисел.
Если существует несколько ответов, минимизирующих максимальное число, то разрешается вывести любой из них.
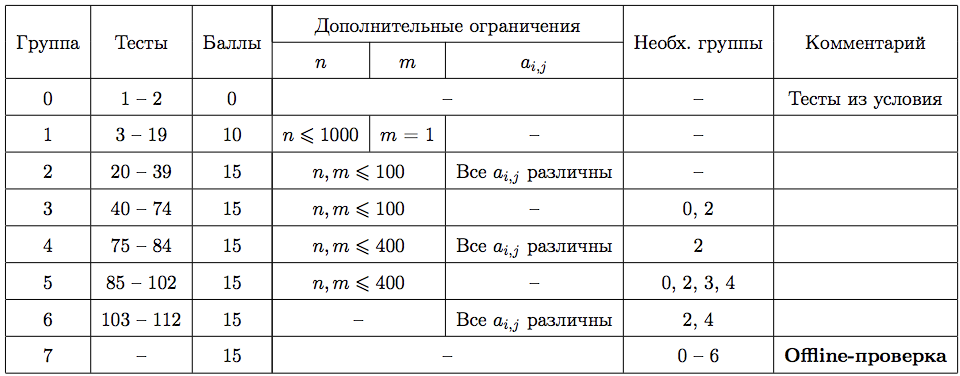
Тесты к этой задаче состоят из восьми групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
В первом примере a 1, 2 ≠ a 2, 1 , но, поскольку они не располагаются в одной строке или в одном столбце, при сжатии их можно сделать равными.
2 2 1 2 3 4
1 2 2 3
4 3 20 10 30 50 40 30 50 60 70 90 80 70
2 1 3 5 4 3 5 6 7 9 8 7