Паук и паучиха плывут по озеру на двух веточках. Плавать они не умеют, поэтому смогут встретиться только тогда, когда веточки соприкоснутся.
Считая, что веточки имеют форму отрезков, и что они плывут с постоянными скоростями, определите, сколько осталось ждать встречи несчастным членистоногим.
Входной файл содержит 12 чисел: \(x_1\), \(y_1\), \(x_2\), \(y_2\), \(x_3\), \(y_3\), \(x_4\), \(y_4\), \(v_{1x}\), \(v_{1y}\), \(v_{2x}\), \(v_{2y}\). Координаты вершин первого отрезка: (\(x_1\), \(y_1\)) и (\(x_2\), \(y_2\)), координаты вершин второго отрезка: (\(x_3\), \(y_3\)) и (\(x_4\), \(y_4\)), скорость первого отрезка (\(v_{1x}\), \(v_{1y}\)), скорость второго отрезка (\(v_{2x}\), \(v_{2y}\)). Все числа целые и не превосходят по модулю \(10^4\). В начальный момент времени веточки не соприкасаются. Гарантируется, что веточки имеют ненулевую длину.
Выведите в выходной файл время до ближайшего момента, когда веточки соприкоснутся, с ошибкой не более \(10^{-4}\). Если веточки не соприкоснутся никогда, выведите число -1.
0 0 -1 3 4 4 7 7 3 0 0 -1
1.6
0 0 -1 3 4 4 7 7 1 0 0 -3
-1
Числовая последовательность задана рекуррентной формулой: \(a_{i+1}\)=(\(k\) \(a_i\)+\(b\))mod \(m\). Найдите длину её наибольшей возрастающей подпоследовательности.
Программа получает на вход пять целых чисел: длину последовательности \(n\) (1≤\(n\)≤\(10^5\)), начальный элемент последовательности \(a_1\), параметры \(k\), \(b\), \(m\) для вычисления последующих членов последовательности (1≤\(m\)≤\(10^4\), 0≤\(k\)<\(m\), 0≤\(b\)<\(m\), 0≤\(a_1\)<\(m\)).
Требуется вывести длину наибольшей возрастающей подпоследовательности данной последовательности.
5 41 2 1 100
3
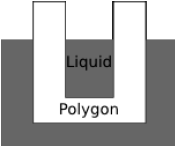
Многоугольник топят в жидкости, опуская его из воздуха с постоянной скоростью v метров в минуту. Жидкость разъедает многоугольник со всех сторон с постоянной скоростью c метров в минуту. Для точки (\(x\), \(y\)) внутри многоугольника, опускающейся вместе с ним, выясните, в какой момент разъедающая жидкость доберётся до этой точки.
Граница между воздухом и жидкостью проходит по прямой \(y\)=0. Жидкость разъедает многоугольник как двумерную фигуру. Многоугольник не поворачивается при опускании в жидкость, и в момент времени 0 он не касается жидкости.
В отличие от многоугольника, который считается двумерным, жидкость существует в трёх измерениях. Поэтому она проникает внутрь «дыр» в многоугольнике. Например, если многоугольник имеет форму «чашки», жидкость проникает «внутрь», как показано на рисунке.
В первой строке входного файла записано через пробел пять целых чисел \(n\), \(x\), \(y\), \(v\) и \(c\) (3 \(\le\) \(n\) \(\le\) 30, −100 \(\le\) \(x\) \(\le\) 100, 1 \(\le\) \(y\) \(\le\) 100, 1 \(\le\) \(c\) < \(v\) \(\le\) 100). Следующие \(n\) строк описывают вершины многоугольника; \(i\)-я из них содержит два целых числа \(x\) и \(y\) через пробел (−100 \(\le\) \(x\) \(\le\) 100, 1 \(\le\) \(y\) \(\le\) 100). Вершины даны в порядке обхода против часовой стрелки. Многоугольник не имеет самопересечений и самокасаний, а точка (\(x\), \(y\)) лежит строго внутри него.
Выведите одно число — время, которое потребуется жидкости, чтобы добраться до точки (\(x\), \(y\)), с точностью не менее четырёх знаков после запятой.
4 0 50 2 1 -1 10 1 10 1 90 -1 90
25.8660
Ваша задача — найти все вхождения данной строки в длинный текст.
Входной файл начинается со строки, которую нужно искать. Все символы входного файла до звёздочки * — строка, которую нужно искать. Все символы, начиная с первой звёздочки и до конца файла — текст, в котором нужно искать.
Все символы с ASCII кодами 33126 (кроме «*») допустимы и могут встречаться как в строке, так и в тексте. Все пробелы и символы перевода строки во входном файле должны игнорироваться.
Длина строки не превосходит 10000, а длина текста не превосходит 200000 символов.
Выведите в выходной файл в возрастающем порядке все точки вхождения данной строки в данный текст. Точка вхождения — это количество символов от начала текста до первого символа вхождения, увеличенное на 1. Если вхождение начинается сразу после звездочки, то точка его вхождения равна 1.
aa* bb aaa
3 4
На клетчатом поле \(N\times N\), некоторые клетки которого закрашены, требуется найти размер максимального квадрата, состоящего из закрашенных клеток.
В первой строке входного файла содержится единственное целое число \(N\) (\(1\le N\le 3\,000\)). В каждой из следующих \(N\) строк содержится по \(N\) символов «#» и «.» (соответствующих закрашенным и незакрашенным клеткам соответственно), описывающих таблицу.
Выведите единственное целое число — максимальный размер полностью закрашенного квадрата.
Каждая программа тестируется на четырёх тестах:
чтобы пройти первый тест, достаточно написать решение, работающее за \(O(N^5)\), чтобы пройти второй, требуется решение уже за \(O(N^4)\), третий — за \(O(N^3)\), четвёртый — за \(O(N^2\log N)\).
За каждый успешно пройденный тест начисляется 25 баллов.
Посылка, набирающая \(x\) баллов по сумме баллов за тесты, считается принятой, если выполняются следующие два условия:
* во-первых, если \(x>25\), должна существовать более ранняя принятая посылка, балл за которую по сумме баллов за тесты равен \(x-25\),
* во-вторых, программа не должна содержать отсечений по \(N\), искусственных замедлений работы и т. п.
Если посылка не принята, через некоторое время после её отправки результат её проверки станет «Дисквалифицирован». Балл за принятую попытку вычисляется как сумма баллов за каждый тест минус 5 баллов за каждую более раннюю дисквалифицированную посылку.
Задача считается решённой, если существует принятая посылка, получившая не менее 100 баллов.
Проще говоря, нужно честно последовательно сдать сначала решение, проходящее только первый тест, затем решение, проходящие первые два теста, затем — все тесты, кроме последнего, и, наконец, решение, проходящее все тесты. При этом допускаются ошибки в программах, уменьшающие балл, но для каждой асимптотики должно быть сдано хотя бы одно своё верное решение.