Бинарный поиск(101 задач)
Порядковые статистики(3 задач)
Поиск подстроки в строке(1 задач)
Тернарный поиск(8 задач)
"Два указателя"(18 задач)
Палиндром - это слово, которое читается справа налево также, как слева направо. Например, "a", "abba", "anavolimilovana" - палиндромы.
Весом строки, состоящей из строчных латинских символов будем называть количество ее подстрок (слов), являющихся палиндромами (при этом каждое вхождение подстроки считается отдельно). Формально, пусть W - строка длины N . Слово w a , b - подстрока W , состоящая из символов на позициях с индексами с a по b включительно. Вес строки W - это количество пар целых чисел a , b ( 1 ≤ a , b ≤ N ) таких, что w a , b является палиндромом.
Вам дана строка, состоящая из строчных латинских символов. Вы можете либо оставить ее неизменной, либо поменять любой из ее символов на любой другой символ. Найдите максимально возможный вес строки, которую вы можете получить.
Первая строка содержит одну строку W ( 1 ≤ | W | ≤ 100000 ), состоящую из строчных латинских символов.
Выведите одно целое число - максимально возможный вес.
Решения, работающие при
|
W
| ≤ 100
, будут оцениваться в 17 баллов.
Решения, работающие при
|
W
| ≤ 5000
, будут оцениваться еще в 37 баллов.
aaaa
10
baccb
9
slavko
7
Знаменитый художник Вася только что закончил работу над своим новым шедевром и хочет знать, сколько он сможет получить за свой труд.
Картина представляет собой прямоугольник N на M сантиметров, разделенный на маленькие квадратики 1 на 1 сантиметр со сторонами, параллельными сторонам картины. Для достижения гармонии каждый из этих квадратиков Вася покрасил одним из 26 особых цветов, обозначаемых маленькими латинскими буквами.
Стоимость картины в точности равна количеству «симпатичных» частей в ней. Частью картины называется любой прямоугольник, который может быть вырезан из нее по границам квадратиков. Часть называется «симпатичной», если при выполнении симметрии относительно ее центра получается прямоугольник, раскрашенный также, как и исходная часть. Например, в картине, раскрашенной так:
abc
acb
симпатичными являются все части, состоящие из одного квадратика (их 6), а также части
bc acb и a
Напишите программу, которая по информации о шедевре Васи определит его стоимость.
В первой строке содержатся два числа N и M ( 1 ≤ N , M ≤ 300 ). В следующих N строках идут строки, состоящие из M маленьких латинских символов. Символ в i -й строке j -м столбце определяет цвет соответствующего квадратика картины.
Выведите стоимость шедевра — количество частей, симметричных относительно своего центра.
n, m < 10 -> 20 баллов
n, m < 50 -> 30 баллов
n, m < 100 -> 20 баллов
n, m < 300 -> 30 баллов
Этот пример разобран в условии
Симпатичными являются шесть частей 1 × 1 , одна часть 1 × 2 и сама картина.
2 3 abc acb
8
3 2 ab cc ba
8
Как известно, в июне во Флатландии будет проходить чемпионат Юпитера по футболу. В турнире примут участие n команд, а сам турнир будет разыгран в один круг, в ходе которого каждая команда сыграет с каждой другой командой.
На Юпитере выпускают футбольную форму m цветов. Каждая команда привезёт с собой два комплекта формы различных цветов. Разумеется, во время матча все игроки одной команды должны быть одеты в форму одного цвета, отличного от цвета формы другой команды.
Для судейства всех матчей этого чемпионата был приглашён глава Фантастической Инопланетной Футбольной Ассоциации Йозеф. Перед началом матча Йозеф назначает каждой из команд цвет футболок, в которых игроки выйдут на поле. Разумеется, выбирать можно только из тех двух цветов футболок, которые привезла с собой команда. После этого Йозеф выбирает себе футболку какого-то цвета, отличного от обоих цветов, в которых будут играть команды. Таким образом, обе команды и судья будут находиться на поле в футболках разного цвета. Любую футболку и команды, и Йозеф могут использовать в неограниченном количестве игр чемпионата.
Футболки для судейства Йозеф закупает непосредственно перед чемпионатом, опираясь на знание о цветах футболок, привезённых командами на турнир. Поскольку Йозеф экономит деньги своей федерации, он хочет купить себе минимальное количество футболок, такое что их хватит для обслуживания всех матчей. Данная задача слишком сложна для обычного футбольного судьи, поэтому он обратился за помощью к вам.
В первой строке входных данных записаны два числа n и m ( 2 ≤ n ≤ 100 000, 2 ≤ m ≤ 10 9 ) — количество команд, участвующих в чемпионате, и количество возможных цветов футболок.
В i -й из следующих n строк записаны два различных целых числа от 1 до m — цвета футболок, которые привезла с собой команда с номером i .
В первой строке выведите минимальное количество футболок, которого хватит Йозефу, чтобы обслужить встречи всех пар команд. Если решения не существует, то выведите одну строку содержащую -1 .
В следующей строке выведите цвета этих футболок.
Если оптимальных решений несколько, разрешается вывести любое из них.
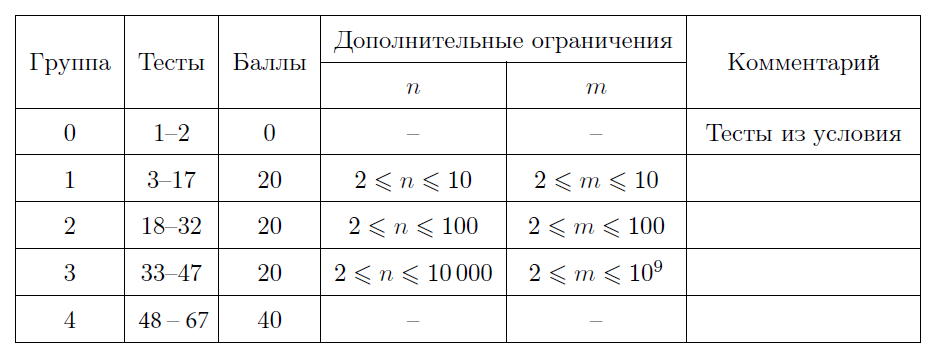
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
3 4 1 2 2 3 1 4
1 1
5 3 1 2 2 3 2 3 3 1 1 2
2 3 1
Злой Конь объявляет набор в Злую Лигу Зла! Он начертил своим копытом на бумаге длинную строку s , состоящую только из символов « ( », « ) » и « ? » и послал всем потенциальным кандидатам. Желающий подать заявку в злодеи должен для каждого символа « ? » выбрать: заменить его на открывающую скобку или на закрывающую. В Злую Лигу Зла попадёт тот из них, у кого в получившейся строке можно будет выделить самую длинную подпоследовательность , являющуюся правильной скобочной последовательностью.
Подпоследовательностью строки называется строка, получающаяся из данной удалением какого-то (возможно нулевого) количества символов. Например, строки « abc », « ac », « bcc » и « abbcc » являются подпоследовательностями строки « abbcc », а строки « cb » и « ba » не являются. Обратите внимание, пустая строка является подпоследовательностью любой строки.
Последовательность круглых скобок называется правильной в следующих случаях:
Например, последовательности круглых скобок « ()() » и « ((()))() » являются правильными, а « )(() », « ((((( » и « ()) » — нет.
Доктор Хоррибл уже давно мечтает попасть в Злую Лигу Зла, но из-за его пацифизма у него не очень-то хорошо выходит совершать злые поступки. Решает задачи Доктор Хоррибл тоже неважно, поэтому попросил вас помочь ему справиться с головоломкой от Злого Коня.
В единственной строке входных данных содержится строка s ( 1 ≤ | s | ≤ 10 000 000 ). Гарантируется, что строка s состоит только из символов « ( », « ) » и « ? ».
Выведите решение задачи Злого Коня, благодаря которому Доктор Хоррибл точно попадёт в Злую Лигу Зла. То есть замените « ? » на « ( » или « ) » таким образом, чтобы длина самой длинной правильной скобочной подпоследовательности, которую можно выделить в этой строке, была максимальной. Если оптимальных ответов несколько, разрешается вывести любой.
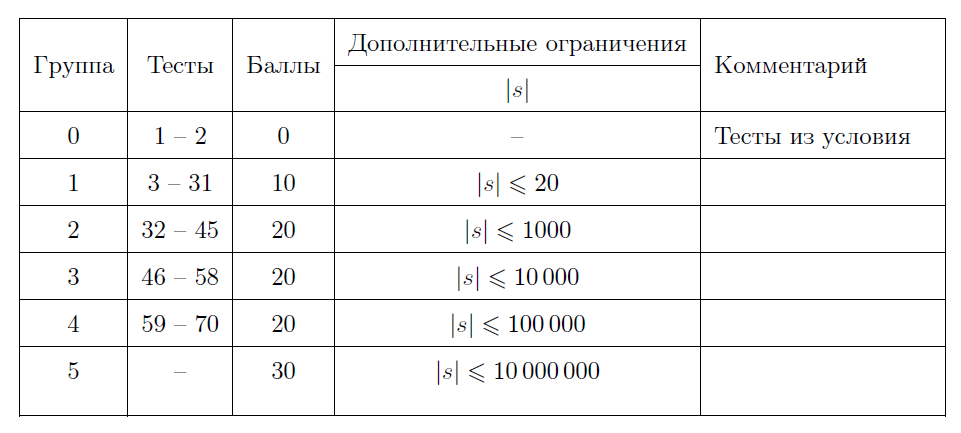
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
В первом тесте из результирующей строки можно после замены вопросов выделить правильную скобочную подпоследовательность длины 4 : « ()() ».
Во втором тесте из результирующей строки можно выделить правильную скобочную подпоследовательность длины 4 : « (()) ». Обратите внимание, возможны и другие варианты ответа.
?)))?)
()))()
)(???)(
)((())(
Дима архитектор. А ещё Дима фотограф. Он часто носится по свету и фотографирует местные Биг Бены и прочие крутые сооружения.
На этот раз Дима приехал в Берляндию, знаменитую своим метрополитеном. Он состоит из n линий, каждая из которых представлена прямой на карте города. На пересечении каждых двух линий метрополитена расположены станции, наземные павильоны которых признаны национальными памятниками архитектуры. Как только Дима увидел их с экрана своего смартфона, он мгновенно загорелся желанием их сфотографировать.
Специально для этой цели он решил воспользоваться маршрутным вертолётом, с которого планирует осуществлять съёмку. Вертолёты компании летают по t маршрутам. Каждый маршрут представляет собой прямую линию. Дима может сделать фотографию, находясь в любой точке маршрута, однако, чем меньше расстояние до станции, тем больше деталей будет видно на снимке, и он соберёт больше лайков в социальных сетях. Вот тут Диме нужна ваша помощь.
Вам даны n прямых, задающих линии метро, и t прямых, задающих доступные вертолётные маршруты. Дима просит для каждого маршрута найти расстояние до ближайшей к нему станции.
Гарантируется, что никакие две линии метрополитена не совпадают и что любые две линии пересекаются, а также, что любые два маршрута пересекаются и что любой маршрут пересекается с любой линией.
В первой строке входного файла находятся два числа n и t ( 2 ≤ n ≤ 100 000 , 1 ≤ t ≤ 20 ) — количество линий метро и количество возможных маршрутов, соответственно.
В следующих n строках содержатся по три целых числа a i , b i и c i ( | a i |, | b i | ≤ 10 000 , a i 2 + b i 2 > 0 , | c i | ≤ 10 8 ), описывающие линии метро. Каждая линия представляет собой прямую a i · x + b i · y + c i = 0 .
Затем следуют t строк с описанием возможных вертолётных маршрутов, каждая из них содержит три целых числа u i , v i , w i ( | u i |, | v i | ≤ 10 000 , u i 2 + v i 2 > 0 , | w i | ≤ 10 8 ). Аналогично, каждый маршрут представляет собой прямую u i · x + v i · y + w i = 0 .
Для каждого маршрута выведите единственное вещественное число — расстояние между
i
-м вертолётным маршрутом и наиболее близкой к нему станцией. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность относительно ответа жюри не будет превосходить
10
- 9
, то есть,
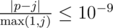 , где
p
— ответ участника, а
j
— ответ жюри.
, где
p
— ответ участника, а
j
— ответ жюри.
Тесты по данной задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп кроме, возможно, тестов из условия.
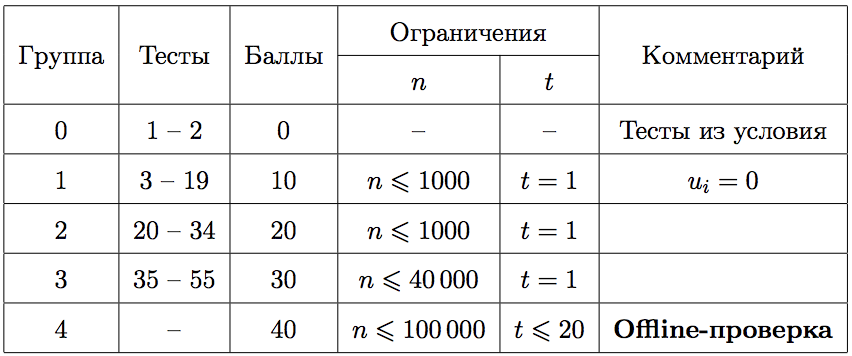
Изображения к тестами из условия приведены ниже.
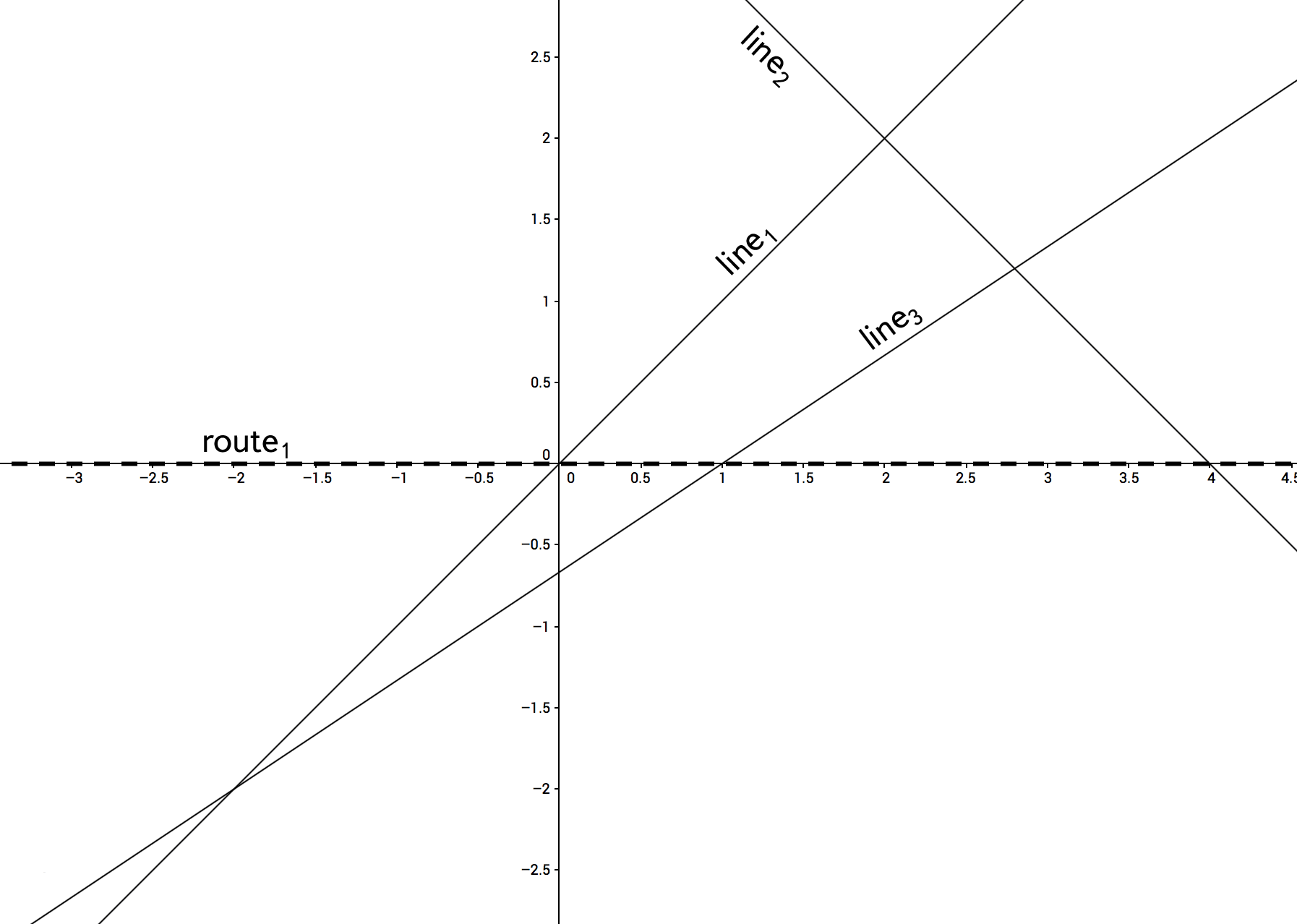
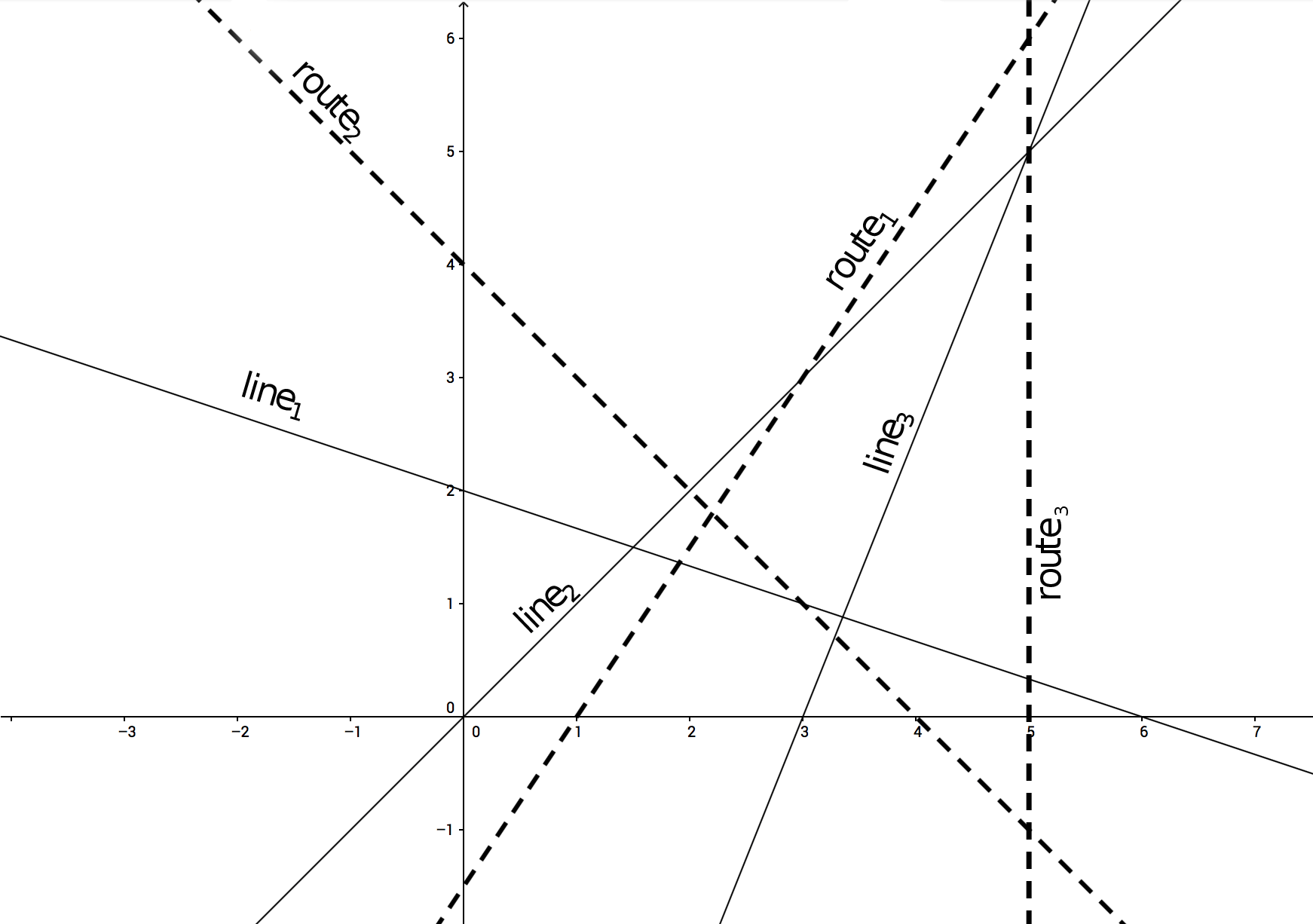
3 1 1 -1 0 1 1 -4 4 -6 -4 0 1 0
1.20000000000000000000
3 3 1 3 -6 -1 1 0 -5 2 15 3 -2 -3 -1 -1 4 1 0 -5
0.41602514716892186000 0.16637806616154061000 0.00000000000000000000