Бинарный поиск по ответу(56 задач)
Бинарный поиск значения функции(5 задач)
В НИИ метеорологии решили изучить процесс образования водоемов на различных рельефах местности во время дождя. Ввиду сложности реальной задачи была создана двумерная модель, в которой местность имеет только два измерения — высоту и длину. В этой модели рельеф местности можно представить как N-звенную ломаную c вершинами \((x_0, y_0), ..., (x_N, y_N)\), где \(x_0 < x_1 < ... < x_N\) и \(y_i \neq y_j\), для любых \(i \neq j\). Слева в точке \(x_0\) и справа в точке \(x_N\) рельеф ограничен вертикальными горами огромной высоты.
Если бы рельеф был горизонтальным, то после дождя вся местность покрылась бы слоем воды глубины H. Но поскольку рельеф — это ломаная, то вода стекает и скапливается в углублениях, образуя водоемы.
Требуется найти максимальную глубину в образовавшихся после дождя водоемах.
В первой строке расположены натуральное число \(N (1 \le N \le 100)\) и \(H\) — действительное число, заданное с тремя цифрами после десятичной точки \((0 \le H \le 10^9)\). В последующих \(N + 1\) строках — по два целых числа \(x_i, y_i: -10000 \le x_i, y_i \le 10000 (0 \le i \le N)\).
Числа в строках разделены пробелами.
Ответ должен содержать единственное число — искомую глубину с точностью до 4-х знаков после десятичной точки.
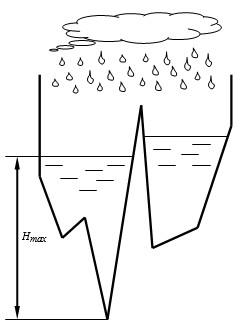
7 7.000 -5 10 -3 4 -1 6 1 -4 4 17 5 3 9 5 12 15
15.8446
В далекой стране есть N городов. Был избран новый премьер-министр. В настоящее время в этой стране нет ни одной дороги, поэтому премьер-министр решил модернизировать страну, соединив некоторые города с двусторонними автострадами в транспортные сети. Два города будут расположены в одной и той же сети, если можно добраться до одного города от другого, используя недавно построенные дороги. Каждый город будет расположен в какой-то сети. Каждая сеть состоит из одного или нескольких городов.
Города представлены в виде точек в двумерной системе координат. Дорога между двумя городами представлена в виде отрезка, соединяющего две точки, в которых расположены города. Длина дороги равна длине отрезка в километрах.
В настоящее время страна переживает экономический спад, поэтому премьер-министр решил, что из-за отсутствия бюджета они не будут строить дороги длиннее, чем D километров. Кроме того, премьер-министр радуется мелочам, поэтому он будет счастлив, если по крайней мере в одной сети будет существовать непустое подмножество городов (оно может включать все города в сети), где общая сумма жителей делится на К . Например, если K = 4 и есть сеть с городами, в которых есть 3 , 5 , 7 жителей соответственно, премьер-министр будет счастлив, потому что сумма жителей в первых двух городах равна 8 .
Помогите премьер-министру сократить расходы, определив минимальный уровень D , необходимый для того чтобы премьер-министр мог строить дороги и одновременно быть счастливым.
Первая строка ввода содержит целые числа N и K (1 ≤ N ≤ 50000, 1 ≤ K ≤ 30) . Каждая из следующих N строк содержит три целых числа x i ; y i ; k i (0 ≤ x i , y i , k i ≤ 100000000) , которые представляют координату x города, координату y и количество жителей в этом городе, соответственно. На входных данных не будет двух городов с одинаковыми координатами. Кроме того, не будет ни одного города, в котором число жителей делится на К .
Первая и единственная строка вывода должна содержать минимальную D с точностью до 3 -х знаков после запятой, такую, что можно строить дороги с условием, что премьер-министр будет счастлив. Входные данные будут такими, чтобы всегда было решение.
Объяснение первого примера: единственный способ удержать премьер-министра в счастливом настроение - все города должны находятся в одном округе. Минимальный D , для которого это возможно, равен 1.414 .
Объяснение второго примера: премьер-министр будет рад, если первые 5 городов находятся в одном округе. Если D = 5.657 , премьер-министр может соединить города 1, 2, 3, 5 с городом 4 . В этом случае сумма жителей в городах 1, 2, 3, 4, 5 составит 11 , что делится на 11 , Поэтому премьер-министр будет счастлив.
3 3 0 4 4 1 5 1 2 6 1
1.414
6 11 0 0 1 0 1 2 1 0 3 1 1 4 5 5 1 20 20 10
5.657
6 5 20 20 9 0 0 3 0 1 1 10 0 1 10 1 6 12 0 3
2.000
На родной планете Чубакки растет очень большое дерево, на ветках которого вуки строят свои домики. Чубакке стало интересно, как быстро можно попасть из некоторых домиков в другие. Вам придется ответить на несколько его вопросов, чтобы он вас отпустил.
Вам дано дерево с N вершинами порядка K , то есть каждая вершина дерева может иметь не более K потомков. Дерево создано по принципу "минимальной энергии": вершины в нем располагается на новом уровне только тогда, когда все места на предыдущем уровне (слева направо) заняты. В таком же порядке вершины дерева пронумерованы, начиная с 1.
Вам необходимо ответить на Q запросов вида " x y ", где ответом является расстояние (количество ребер в минимальном пути) в данном дереве между вершинами с номерами x и y .
Первая строка содержит три целых числа: N ( 1 ≤ N ≤ 10 15 ), K ( 1 ≤ K ≤ 1000 ) и Q ( 1 ≤ Q ≤ 100000 ). Каждая из следующих Q строк содержит пару чисел x y ( 1 ≤ x , y ≤ N , x ≠ y ) - запросы, описанные в условии.
Выведите Q строк, в каждой из которых одно целое число - ответ на соответствующий запрос.
Решения, работающие при 1 ≤ N , Q ≤ 1000 , будут оцениваться в 20 баллов. Решения, работающие при 1 ≤ N , Q ≤ 100000 , будут оцениваться в 50 баллов.
7 2 3 1 2 2 1 4 7
1 1 4
9 3 3 8 9 5 7 8 4
2 2 3
Палиндром - это слово, которое читается справа налево также, как слева направо. Например, "a", "abba", "anavolimilovana" - палиндромы.
Весом строки, состоящей из строчных латинских символов будем называть количество ее подстрок (слов), являющихся палиндромами (при этом каждое вхождение подстроки считается отдельно). Формально, пусть W - строка длины N . Слово w a , b - подстрока W , состоящая из символов на позициях с индексами с a по b включительно. Вес строки W - это количество пар целых чисел a , b ( 1 ≤ a , b ≤ N ) таких, что w a , b является палиндромом.
Вам дана строка, состоящая из строчных латинских символов. Вы можете либо оставить ее неизменной, либо поменять любой из ее символов на любой другой символ. Найдите максимально возможный вес строки, которую вы можете получить.
Первая строка содержит одну строку W ( 1 ≤ | W | ≤ 100000 ), состоящую из строчных латинских символов.
Выведите одно целое число - максимально возможный вес.
Решения, работающие при
|
W
| ≤ 100
, будут оцениваться в 17 баллов.
Решения, работающие при
|
W
| ≤ 5000
, будут оцениваться еще в 37 баллов.
aaaa
10
baccb
9
slavko
7
Злой Конь объявляет набор в Злую Лигу Зла! Он начертил своим копытом на бумаге длинную строку s , состоящую только из символов « ( », « ) » и « ? » и послал всем потенциальным кандидатам. Желающий подать заявку в злодеи должен для каждого символа « ? » выбрать: заменить его на открывающую скобку или на закрывающую. В Злую Лигу Зла попадёт тот из них, у кого в получившейся строке можно будет выделить самую длинную подпоследовательность , являющуюся правильной скобочной последовательностью.
Подпоследовательностью строки называется строка, получающаяся из данной удалением какого-то (возможно нулевого) количества символов. Например, строки « abc », « ac », « bcc » и « abbcc » являются подпоследовательностями строки « abbcc », а строки « cb » и « ba » не являются. Обратите внимание, пустая строка является подпоследовательностью любой строки.
Последовательность круглых скобок называется правильной в следующих случаях:
Например, последовательности круглых скобок « ()() » и « ((()))() » являются правильными, а « )(() », « ((((( » и « ()) » — нет.
Доктор Хоррибл уже давно мечтает попасть в Злую Лигу Зла, но из-за его пацифизма у него не очень-то хорошо выходит совершать злые поступки. Решает задачи Доктор Хоррибл тоже неважно, поэтому попросил вас помочь ему справиться с головоломкой от Злого Коня.
В единственной строке входных данных содержится строка s ( 1 ≤ | s | ≤ 10 000 000 ). Гарантируется, что строка s состоит только из символов « ( », « ) » и « ? ».
Выведите решение задачи Злого Коня, благодаря которому Доктор Хоррибл точно попадёт в Злую Лигу Зла. То есть замените « ? » на « ( » или « ) » таким образом, чтобы длина самой длинной правильной скобочной подпоследовательности, которую можно выделить в этой строке, была максимальной. Если оптимальных ответов несколько, разрешается вывести любой.
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
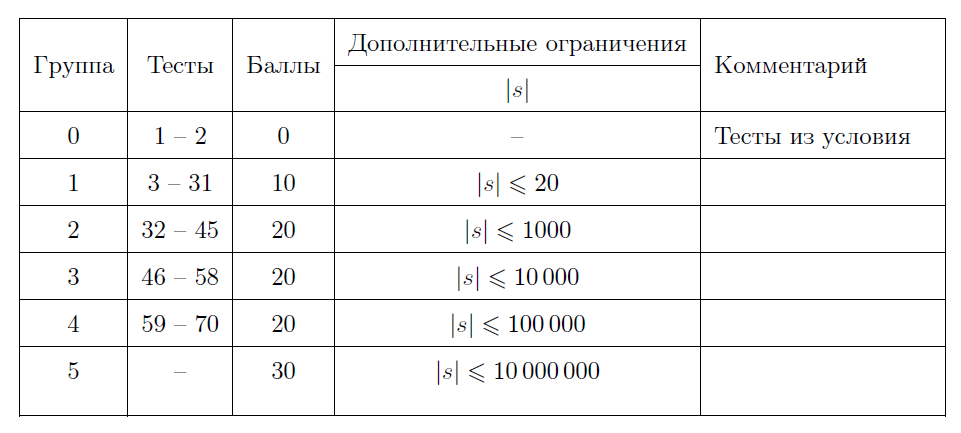
В первом тесте из результирующей строки можно после замены вопросов выделить правильную скобочную подпоследовательность длины 4 : « ()() ».
Во втором тесте из результирующей строки можно выделить правильную скобочную подпоследовательность длины 4 : « (()) ». Обратите внимание, возможны и другие варианты ответа.
?)))?)
()))()
)(???)(
)((())(