В Шахматной Стране всегда пользовались популярностью различные спортивные соревнования: ферзебол, рокировочная борьба, эндшпилевые бега. Но наибольшую популярность в этом году получила спортивная игра «обмен королей».
Суть её заключается в следующем. Двух королей (белого и чёрного) ставят на прямоугольное шахматное поле, некоторые клетки которого отмечены как недостижимые. По правилам игры короли делают ходы по очереди (сначала белый, а затем чёрный), не наступая на недостижимые клетки. Игра считается успешно законченной, если черный и белый короли поменялись местами. В соревновании побеждает та пара королей, которая смогла поменяться местами за минимальное количество ходов.
Напомним, что в шахматах король имеет право переместиться из своей клетки в любую из 8 соседних по вертикали, диагонали или горизонтали, при условии, что она не является соседней для другого короля.
Напишите программу, которая по информации о доске найдет минимальное количество ходов, необходимое для успешного окончания игры.
В первой строке входных данных даны целые числа N и M (1 ≤ N, M ≤ 8) — размеры доски по вертикали и по горизонтали, соответственно. В следующих N строках даны M символов — состояние доски в начале игры. Символ «.» обозначает пустую клетку, символ «*» — недостижимую клетку, символ «W» — белого короля, «B» — черного короля. Гарантируется, что символы «W» и «B» встречаются на поле ровно по одному разу, и короли не находятся в соседних клетках изначально.
В выходной файл необходимо вывести минимальное количество ходов, которое потребуется для того, чтобы белый король поменялся местами с чёрным. В случае, если поменять королей местами невозможно, требуется вывести «Impossible» без кавычек.
4 3
*.*
W.B
...
*.*
8
2 3
W..
..B
Impossible
Последовательность ходов, необходимая для обмена королей в первом тесте, приведена на рисунке:
Во время летних каникул Вася и Петя путешествовали со своими родителями по Одной Очень Гостеприимной Стране. В этой стране всего N городов, пронумерованных числами от 1 до N. Маршрут Васи начинался в городе A и заканчивался в городе B, а маршрут Пети – начинался в городе C и заканчивался в городе D. Поскольку времени у них было немного, то и Васины и Петины родители выбрали самый короткий путь, соединяющий начальный и конечный города их маршрута.
После каникул Вася с Петей встретились и захотели обсудить свои путешествия. Особенно интересно было обсуждать те города, в которых побывали они оба.
Определите, в каких городах побывали и Вася и Петя и выведите их номера в порядке возрастания. Если же маршруты ребят не пересекались, выведите -1.
Обратите внимание на то, что поскольку на некоторых дорогах шел ремонт, то длина пути от города X в город Y может отличаться от длины пути от города Y в город X.
В первой строке вводится число N (1 ≤ N ≤ 100). В следующих N строках вводится по N чисел, не превосходящих 100, j-ое число в i-ой строке равно длине пути между i-м и j-м городом. Известно, что между любыми двумя городами есть дорога и поскольку на некоторых дорогах идет ремонт, то длина пути от города X в город Y может отличаться от длины пути от города Y в город X. В следующих двух строках вводятся пары целых числа от 1 до 100 – номера городов, являющихся началом и концом маршрута Васи (A и B), и аналогичные числа для Пети (C и D).
Выведите их номера в порядке возрастания. Если маршруты ребят не пересекались, выведите одно число - 1. Гарантируется, что кратчайший путь – единственный.
4
0 100 100 1
100 0 3 100
100 4 0 1
100 3 10 0
1 3
2 3
2 3
В сказочной стране, столицей которой является Изумрудный Город, всего N городов. Некоторые города соединены дорогой, целиком вымощеной желтым кирпичем. Элли нужно добраться из города на границе в Изумрудный Город и затем вернуться обратно. Чтобы не было скучно, ей хочется добираться туда и обратно разным маршрутом (а именно так, чтобы ни одна из дорог не была и на маршруте туда и на маршруте обратно). Поскольку зря тратить время она не собирается, то для каждого пути она хочет выбрать самый короткий вариант.
Напишите программу, которая поможет Элли определить, возможно ли такое путешествие, и если оно возможно, то разработает для нее маршрут.
Все города пронумерованы натуральными числами от 1 до N, город на границе имеет номер K, Изумрудный Город имеет номер N.
В первой строке содержатся три числа: N, K и M (1 ≤ N ≤ 100, 1 ≤ K < N,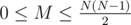 
), где N -– количество городов в Сказочной стране, K – номер города, из которого Элли начинает путешествие, M – количество дорог, мощеных желтым кирпичем. В следующих M строках вводятся по три числа – номера городов, соединенных дорогой из желтого кирпича и длина этой дороги.
В первой строке выведите -1, если желание Элли неосуществимо. В противном случае в первой строке выведите два числа: длину пути туда и длину пути обратно, а в следующих двух строках: номера городов на пути туда и на пути обратно в том порядке, в котором она будет их проходить.
4 1 6
1 4 3
2 4 2
2 3 1
1 2 5
1 3 6
4 3 8
3 7
1 4
4 2 1
4 1 0
-1
В столице одной небольшой страны очень сложная ситуация. Многокилометровые пробки буквально парализовали движение в городе, и власти на многих улицах ввели одностороннее движение, не анализируя, можно ли будет теперь проехать из любого места в городе в любое другое, не нарушая правила. Транспортная система столицы представляет собой N площадей, соединенных M полосами для движения, в том числе круговыми полосами, проходящими по площади. Каждая полоса предназначена для движения только в одну определенную сторону. При этом на магистралях есть полосы, направленные как в одну, так и в другую сторону. По круговой полосе можно двигаться только внутри площади и только против часовой стрелки.
Власти города на каждой полосе разместили видеокамеру, поэтому если Иннокентий едет по встречной полосе (при ее наличии) или, в случае одностороннего движения, в сторону противоположную предписанной знаками, то после поездки против правил по каждой из полос ему придется заплатить штраф в размере одной тысячи тугриков этой страны.
Иннокентий, который торопится купить кафельную плитку со скидкой, решился доехать до магазина в любом случае, даже если для этого придется нарушать правила. Но он хочет выбрать такой маршрут движения, суммарный штраф на котором минимален.
Иннокентий еще не решил, откуда именно и в какой магазин он собирается ехать, поэтому ему необходимо ответить на несколько вопросов вида «Какой минимальный штраф надо заплатить, чтобы добраться из пункта A в пункт B?». Отвечая на потребности жителей столицы, известная поисковая система Индекс разрабатывает соответствующий сервис.
Так как многие из вас рано или поздно будут проходить собеседование на работу в эту фирму, продемонстрируйте, что вы тоже умеете решать эту задачу.
В первой строке входных данных содержатся два числа N и M — количество площадей и полос движения в городе соответственно (1 ≤ N ≤ 5000, 1 ≤ M ≤ 10 000). Далее содержатся описания полос, по которым движение разрешено. Каждая полоса описывается номерами двух площадей, которые она соединяет. Движение разрешено в направлении от первой из указанных площадей ко второй.
В следующей строке содержится одно число K — количество вопросов у Иннокентия (1 ≤ K ≤ 10 000, N·K ≤ 2·107). В следующих строках описываются вопросы, каждый вопрос описывается номерами двух площадей, между которыми требуется найти самый дешевый путь. Путь необходимо проложить от первой из указанных площадей ко второй.
Для каждого вопроса выведите одно число — искомый минимальный размер штрафа в тысячах тугриков. В случае, если пути между выбранной парой площадей не существует, выведите - 1.
Тесты к этой задаче состоят из четырех групп.
Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы.
5 5 2 1 2 4 3 2 4 3 5 4 3 5 1 1 5 2 3
0 2 0
В неориентированном графе требуется найти длину минимального пути между двумя вершинами.
Первым на вход поступает число N –– количество вершин в графе ( 1 ≤ N ≤ 100 ). Затем записана матрица смежности (0 обозначает отсутствие ребра, 1 –– наличие ребра). Далее задаются номера двух вершин –– начальной и конечной.
Выведите L –– длину кратчайшего пути (количество ребер, которые нужно пройти). Если пути не существует, выведите одно число - 1 .
5 0 1 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 3 5
3