Алгоритм Флойда(20 задач)
Обход в ширину(62 задач)
Алгоритм Форда-Беллмана(6 задач)
В одном из уровней компьютерной игры вы попали в лабиринт, состоящий из n строк, каждая из которых содержит m клеток. Каждая клетка либо свободна, либо занята препятствием. Стартовая клетка находится в строке r и столбце c . За один шаг вы можете переместиться на одну клетку вверх, влево, вниз или вправо, если она не занята препятствием. Вы не можете перемещаться за границы лабиринта.
К сожалению, ваша клавиатура крайне близка к поломке, поэтому вы можете переместиться влево не более x раз и вправо не более y раз. При этом ограничений на перемещения вверх и вниз нет, поскольку клавиши, используемые для движения вверх и вниз, всё ещё в идеальном состоянии.
Теперь вы для каждой клетки поля решили установить, можно ли выбрать такую последовательность нажатий, которая приведёт вас из стартовой в эту клетку. Посчитайте, сколько клеток поля обладают таким свойством.
Первая строка содержит два целых числа n , m ( 1 ≤ n , m ≤ 2000 ) — количество строк и столбцов в лабиринте, соответственно.
Вторая строка содержит два целых числа r , c ( 1 ≤ r ≤ n , 1 ≤ c ≤ m ) — номер строки и столбца, на пересечении которых расположена стартовая клетка.
Третья строка содержит два целых числа x , y ( 0 ≤ x , y ≤ 10 9 ) — максимальное количество перемещений влево и вправо, соответственно.
Следующие n строк содержат описание лабиринта. Каждая из этих строк имеет длину m и состоит только из символов ' . ' и ' * '. В i -й строке j -й символ соответствует клетке лабиринта с номерами строки и столбца i и j , соответственно. Символ ' . ' соответствует свободной клетке лабиринта, а символ ' * ' — клетке с препятствием.
Гарантируется, что стартовая клетка не занята препятствием.
Выведите одно число — количество клеток лабиринта, достижимых из стартовой, включая её саму.
Клетки, достижимые в соответствующем примере, отмечены ' + '.
Первый пример
+++..
+***.
+++**
*+++.
Второй пример
.++.
.+*.
.++.
.++.
4 5 3 2 1 2 ..... .***. ...** *....
10
4 4 2 2 0 1 .... ..*. .... ....
7
На дворе \(3020\) год. Король Байтазар правит огромной планетарной системой, в которой насчитывается целых \(n\) планет. В \(3020\) году люди отказались от традиции давать планетам имена и вместо этого используют номера. Дворец Байтазара находится на планете под номером \(1\), в то время как его военная база находится на планете под номером \(2\). Давным давно для Байтазара был построен портал, соединяющий планеты \(1\) и \(2\), который позволяет добираться с планеты номер \(1\) на планету номер \(2\) или обратно за \(250\) минут (немногим больше четырёх часов).
С тех пор технологии шагнули далеко вперёд, и современные порталы позволяют добиратся между планетам всего за \(1\) час (в \(3020\) году в часе всё ещё \(60\) минут). Порталы, разумеется, остались двухсторонними. Некоторые из планет уже соединены современными версиями порталов (но не планеты \(1\) и \(2\) - король Байтазар крайне консервативен). Вообще, уже сейчас возможно добраться от планеты \(1\) до планеты \(2\) используя имеющиеся новые порталы, но личный портал Байтазара остаётся самым быстрым способом добраться между планетами \(1\) и \(2\).
Технология быстрой телепортации продолжает своё распространение и Байтазар хочет это поддержать, не желая между тем менять свой личный портал старого типа на новый. При этом, из соображений безопасности Байтазар не хочет, чтобы был способ добраться с планеты \(1\) на планету \(2\) быстрее, чем его личный портал. Помогите Байтазару. Найдите максимальное число новых порталов, которые можно построить так, чтобы личный портал Байтазара оставался самым быстрым путем перемещения между резиденцией и военной базой.
В первой строке даны два числа \(n\) и \(m\) (\( 2 \le n \le 40000, 1 \le m \le 1000000\)) - количество планет в планетарной системе Байтазара и количество двусторонних порталов нового типа соответственно.
В последующих \(m\) строках дано описания порталов. Каждая строка содержит два целых числа \(v\) и \(u\), (\(1 \le v, u \le n\), \(v \ne u\)), что означает что планеты \(v\) и \(u\) соединены порталом нового типа.
Гарантируется, что существует способ добраться с планеты \(1\) на планету \(2\) используя имеющиеся порталы и что такое путешествие займёт строго больше \(250\) минут.
Выведете единственное число \(ans\) - наибольшее количество порталов которое можно построить в планетарной системы Байтазара, так чтобы личный портал Байтазара оставался самым быстрым путем перемещения между резиденцией и военной базой.
В тестах суммарной стоимостью не менее \(20\) баллов дополнительно гарантируется что \(n \le 8\), \(m \le 9\).
В тестах суммарной стоимостью не менее \(30\) баллов дополнительно гарантируется что \(n \le 12\), \(m \le 20\).
В тестах суммарной стоимостью не менее \(60\) баллов дополнительно гарантируется что \(n \le 150\), \(m \le 4000\).
Иллюстрация к первому примеру:
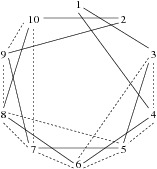
Жирными линиями показаны имеющиеся скоростные порталы, в то время как пунктирными линиями показаны те порталы, которые Байтазар может построить, не подвергнув государство опасности и построив при этом максимально возможное количество скоростных порталов.
10 10 1 3 3 5 5 7 7 9 2 9 1 4 4 6 6 8 8 10 2 10
10