Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.
В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.
Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.
Будем считать, что в городе введена прямоугольная декартова система координат.
Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.
Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10-8). Точки могут лежать как на одной дорожке, так и на разных.
Выведите минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10-4.
Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите число -1.
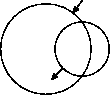
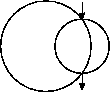
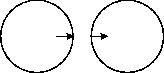
0 0 5 4 0 3 3.0 4.0 1.878679656440357 -2.121320343559643
8.4875540166
0 0 5 4 0 3 4.0 3.0 4.0 -3.0
6.4350110879
0 0 4 10 0 4 4.0 0.0 6.0 0.0
-1
В одном феодальном государстве средневековой Европы было n городов и m дорог, каждая из которых соединяла некоторые два города. Каждая дорога принадлежала правителю одного из городов (не обязательно одного из тех, которые она соединяла). Однажды правитель города S решил объявить войну правителю города T. Перед ним сразу же встала нелегкая задача: как довести армию до города T.
Правитель каждого города требует плату за проход войск через его город. Кроме того, правитель города S может перемещать войска только по дорогам, которые принадлежат ему. При этом он может купить любую дорогу у ее владельца за определенную плату (даже если владелец – правитель города T). К сожалению, все деньги из казны города S были потрачены на предыдущий неудачный военный поход, поэтому сначала правителю придется продать некоторые свои дороги (разумеется, после этого он не сможет провести по ним войска).
Помогите правителю выяснить, какие дороги следует продать, а какие купить, чтобы довести войска от города S до города T и оплатить проход через все промежуточные города. Все операции продажи и покупки дорог надо осуществить до начала похода, пока правители других городов не догадались о воинственных намерениях правителя города S.
В первой строке вводятся целые числа n и m – количество городов и дорог соответственно ( 2
n2 000, 1m50 000). Города нумеруются от 1 до n, города S и T имеют номера 1 и n соответственно.
Следующие n строк содержат под одному целому числу ri – плату за проезд через город i ( 0ri10 000, r1 = rn = 0).
Далее идут m строк, задающих описания дорог. Дорога описывается четырьмя целыми числами: ai, bi, pi и ci. Здесь ai и bi – номера городов, которые соединяет дорога, pi – номер города, правителю которого она принадлежит, ci – ее стоимость ( ai
bi, 1ci10 000). По дороге можно перемещаться в обоих направлениях. Любые два города соединены не более, чем одной дорогой.
В первой строке выведите список дорог, которые нужно продать в следующем формате: сначала число дорог, а затем их номера. Дороги нумеруются с единицы в том порядке, в котором они заданы во входных данных. Во второй строке выведите список дорог, которые нужно купить, в том же формате. В третьей строке выведите маршрут похода – номера городов в порядке следования войска. Если решений несколько, выведите любое.
Если решения нет, выведите число -1.
3 3 0 1 0 1 2 1 10 2 3 1 10 3 1 2 2
2 1 2 1 3 1 3
В точке (0, 0) координатной плоскости расположена лампочка, которая представляет собой точечный источник света. Неподалеку от лампочки находится дом Пети, который представляет собой выпуклый многоугольник с \(N\) вершинами. Сам Петя находится в точке с координатами (\(x\), \(y\)).
Петя хочет увидеть свет. Для этого ему необходимо оказаться в такое точке, что отрезок, соединяющей ее с началом координат, не пересекается с домом Пети (но может его касаться, в частности, проходить вдоль стороны многоугольника дома).
Петя может перемещаться по плоскости со скоростью \(v\). Разумеется, Петя не может проходить сквозь дом (хотя он может двигаться по его границе).
Выясните, какое минимальное время требуется Пете, чтобы оказаться в освещенной точке.
В первой строке вводятся координаты Пети – два неотрицательных вещественных числа, не превышающих 1000, и его скорость v – вещественное число, 10-2\( \le\) v\( \le\) \(10^4\).
Вторая строка содержит \(N\) – число вершин в многоугольнике, задающем Петин дом ( 3\( \le\)N\( \le\)100). Далее в \(N\) строках вводится по два вещественных числа – координаты вершин многоугольника в порядке их обхода против часовой стрелки. Все координаты неотрицательны и не превышают 1000.
Гарантируется, что входные данные корректны, в частности, многоугольник выпуклый, и никакие три его последовательные вершины не лежат на одной прямой. Также гарантируется, что и Петя, и лампочка находятся снаружи от многоугольника, в частности, не находятся на его границе. Расстояние от точки, где находится Петя, до многоугольника и от начала координат до многоугольника не меньше 10-2, расстояние от Пети до начала координат не меньше 10-2.
Выведите минимальное время, за которое Петя сможет попасть в освещенную точку. Ваш ответ должен отличаться от правильного не более чем на 10-4.
3.5 3.5 1.0 4 2.0 0.0 4.0 2.0 2.0 4.0 0.0 2.0
3.58113883008418967000
Между \(N\) населенными пунктами совершаются пассажирские рейсы на машинах времени.
В момент времени 0 вы находитесь в пункте \(A\). Вам дано расписание рейсов. Требуется оказаться в пункте B как можно раньше (то есть в наименьший возможный момент времени).
При этом разрешается делать пересадки с одного рейса на другой. Если вы прибываете в некоторый пункт в момент времени \(T\), то вы можете уехать из него любым рейсом, который отправляется из этого пункта в момент времени \(T\) или позднее (но не раньше).
В первой строке вводится число \(N\) – количество населенных пунктов ( 1\( \le\)N\( \le\)1000). Вторая строка содержит два числа \(A\) и \(B\) – номера начального и конечного пунктов. В третьей строке задается \(K\) – количество рейсов ( 0\( \le\)K\( \le\)1000). Следующие \(K\) строк содержат описания рейсов, по одному на строке. Каждое описание представляет собой четверку целых чисел. Первое число каждой четверки задает номер пункта отправления, второе – время отправления, третье – пункт назначения, четвертое – время прибытия. Номера пунктов – натуральные числа из диапазона от 1 до \(N\). Пункт назначения и пункт отправления могут совпадать. Время измеряется в некоторых абсолютных единицах и задается целым числом, по модулю не превышающим \(10^9\). Поскольку рейсы совершаются на машинах времени, то время прибытия может быть как больше времени отправления, так и меньше, или равным ему.
Гарантируется, что входные данные таковы, что добраться из пункта \(A\) в пункт \(B\) всегда можно.
Выведите минимальное время, когда вы сможете оказаться в пункте \(B\).
2 1 1 2 1 1 2 10 1 10 1 9
0
1 1 1 3 1 3 1 -5 1 -5 1 -3 1 -4 1 -10
-10
5 1 2 6 1 0 3 10 4 2 2 -10 4 14 2 -7 3 10 2 10 2 0 4 2 3 10 4 12
-10
Государство Флатландия представляет собой прямоугольник размером \(M\) × \(N\), состоящий из единичных квадратиков. Флатландия разделена на K провинций (2 <= \(K\) <= 100). Каждая провинция представляет собой связное множество квадратиков, т.е. из каждой точки провинции можно дойти до любой другой ее точки, при этом разрешается переходить с квадратика на квадратик, только если они имеют общую сторону (общей вершины недостаточно). Во Флатландии нет точки, которая граничила бы более чем с тремя провинциями (т.е. четыре квадратика, имеющие общую вершину, не могут принадлежать четырем разным провинциям).
Каждая провинция имеет свой символ. Столица Флатландии находится в провинции, которой принадлежит символ \(A\) (заглавная латинская буква \(A\)). Провинция называется пограничной, если она содержит граничные квадратики. Провинция, в которой находится столица Флатландии, не является пограничной.
Король соседнего с Флатландией королевства Ректилания решил завоевать Флатландию. Для этого он хочет захватить столицу Флатландии. Однако он знает, что сил его армии недостаточно, чтобы сделать это сразу. Поэтому сначала он хочет окружить столичную провинцию, чтобы ослабить силы противника долгой блокадой, а потом захватить столицу.
Чтобы окружить провинцию, требуется захватить все провинции, с которыми она граничит. Две провинции граничат, если существует два квадратика, имеющие общую сторону, один из которых принадлежит первой из них, а другой - второй. Чтобы захватить провинцию, надо чтобы выполнялось одно из двух условий: либо она пограничная, либо граничит с какой-либо уже захваченной провинцией.
Чтобы сберечь силы своей армии, король Ректилании хочет установить блокаду столичной провинции, захватив как можно меньше провинций. Помогите ему выяснить, сколько провинций требуется захватить. Захватывать столичную провинцию нельзя, поскольку для этого сил армии Ректилании пока недостаточно.
В первой строке вводятся числа \(M\) и \(N\) (3 <= \(M\), \(N\) <= 200). Следующие \(M\) строк содержат \(N\) символов каждая и задают карту Флатландии. Символ, находящийся в \(i\) + 1-й строке входных данных на \(j\)-м месте, представляет собой символ провинции, которой принадлежит квадратик (\(i\), \(j\)). Все символы имеют ASCII-код больше 32 (пробела).
Выведите единственное число - количество провинций, которые требуется захватить. Если установить блокаду невозможно, выведите "-1".
3 3 BBB BAB BBB
1