Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах --> Кратчайшие пути в графе --> Алгоритм Дейкстры
---> 33 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#111527
Туда и обратно
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В сказочной стране, столицей которой является Изумрудный Город, всего N городов. Некоторые города соединены дорогой, целиком вымощеной желтым кирпичем. Элли нужно добраться из города на границе в Изумрудный Город и затем вернуться обратно. Чтобы не было скучно, ей хочется добираться туда и обратно разным маршрутом (а именно так, чтобы ни одна из дорог не была и на маршруте туда и на маршруте обратно). Поскольку зря тратить время она не собирается, то для каждого пути она хочет выбрать самый короткий вариант.

Напишите программу, которая поможет Элли определить, возможно ли такое путешествие, и если оно возможно, то разработает для нее маршрут.

Все города пронумерованы натуральными числами от 1 до N, город на границе имеет номер K, Изумрудный Город имеет номер N.

Входные данные

В первой строке содержатся три числа: N, K и M (1 ≤ N ≤ 100, 1 ≤ K < N, 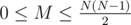), где N -– количество городов в Сказочной стране, K – номер города, из которого Элли начинает путешествие, M – количество дорог, мощеных желтым кирпичем. В следующих M строках вводятся по три числа – номера городов, соединенных дорогой из желтого кирпича и длина этой дороги.

Выходные данные

В первой строке выведите -1, если желание Элли неосуществимо. В противном случае в первой строке выведите два числа: длину пути туда и длину пути обратно, а в следующих двух строках: номера городов на пути туда и на пути обратно в том порядке, в котором она будет их проходить.

Примеры тестов

Входные данные
4 1 6
1 4 3
2 4 2
2 3 1
1 2 5
1 3 6
4 3 8
Выходные данные
3 7
1 4 
4 2 1
Входные данные
4 1 0
Выходные данные
-1

#112600
Не перегораживайте Нил
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

НЛО приземлилось в районе реки, ее вид заворожил инопланетян, потому что на их планете вообще нет рек. Сейчас они хотят построить свой инопланетный поселок на одной из земных рек, но также они знают, что на Земле очень хрупкая экосистема, поэтому нельзя перегораживать реку очень сильно. Но инопланетяне абсолютно не знают, как устроены реки, поэтому они обратились к вам с просьбой написать программу, которая вычислит максимальную пропускную способность реки, после постройки их инопланетного поселка.

Инопланетяне предпочитают строить здания на тех реках, берега которых представляют из себя параллельные прямые, поэтому область реки, где будут строить инопланетяне, можно себе представить как прямоугольную таблицу W × H , у которой каждая клеточка имеет координаты ( X , Y ). Каждая клеточка пропускает через себя 1 кубический метр воды в секунду, и вода может перетекать только между клеточками соседним по стороне. Каждая клеточка на южной стороне реки ( Y = 0 ) имеет приток воды из реки в размере 1 кубический метр воды в секунду. Каждый дом в поселке занимает прямоугольник, состоящий из единичных клеточек; если в клеточке стоит дом, то вода через нее протекать не может. Ваша задача — вычислить, сколько кубических метров за секунду пропускает поселок инопланетян. То есть сколько кубических метров воды вытекает из всех северных клеток поселка ( Y = H - 1 ) в сумме.

Как известно, вода несжимаема, то есть не может накапливаться в клетке, соответственно если в клетку втекло сколько-то воды, то столько же должно и вытечь.

Входные данные

В первой строке содержатся два целых числа W и H — ширина и высота реки соответственно (\(3\leq W \leq 1000;\; 3\leq H \leq 10^{8})\). В следующей строке находится число B — количество домов в поселке инопланетян (\(0 \leq B \leq 1000\)).

Следующие B строк содержат четыре целых координаты X 0 , Y 0 , X 1 , Y 1 . Где X 0 и Y 0 — координаты нижней левой клеточки дома, а X 1 и Y 1 — координаты верхней правой клеточки дома ( 0 ≤ X 0 ≤ X 1 < W и 0 ≤ Y 0 ≤ Y 1 < H ). Домики не перекрываются, но могут касаться по стороне или ребрам.

Выходные данные

Выведите одно число — максимальную пропускную способность поселка в кубических метрах в секунду.

Примечание
Так выглядит поселок для тестов из условия.

Примеры
Входные данные
3 3
2
2 0 2 0
0 2 0 2
Выходные данные
1
Входные данные
5 6
4
1 0 1 0
3 1 3 3
0 2 1 3
1 5 2 5
Выходные данные
2
#113547
Путешествие в Метрополис
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
512 megabytes

Путешествие по стране никогда не бывает простым, особенно когда не существует прямого сообщения между городами. Группа туристов хочет добраться в город Метрополис, используя сеть железных дорог, которая соединяет n городов, пронумерованных от 1 до n. Город, из которого выезжает группа, имеет номер 1, Метрополис имеет номер n.

На железной дороге постоянно функционируют m маршрутов поездов. Каждый маршрут определяется последовательностью городов, перечисленных в том порядке, в каком их проезжает поезд, обслуживающий этот маршрут. В каждом маршруте для каждой пары соседних городов задано время, за которое поезд этого маршрута проезжает перегон между этими городами. При этом поезда разных маршрутов могут проезжать один и тот же перегон за разное время.

По пути в Метрополис группа может садиться на поезд и сходить с поезда в любом городе маршрута, не обязательно в начальном или конечном. При этом, можно сойти с поезда маршрута i, пересесть на поезд маршрута j, возможно сделать еще несколько пересадок, а потом вновь сесть в поезд того же маршрута i.

Туристы предъявляют высокие требования к выбору способа проезда в Метрополис.

Во-первых, суммарное время, проведенное в поездах, должно быть минимальным.

Во-вторых, среди всех способов с минимальным временем нахождения в поездах предпочтительным является тот способ, для которого сумма квадратов промежутков времени, непрерывно проведенных в поезде между двумя пересадками, максимальна. Назовём эту сумму качеством путешествия.

Время, проведенное вне поездов, не учитывается.

Требуется написать программу, которая по описаниям имеющихся маршрутов поездов определит минимальное время, которое группе туристов придется провести в поездах, а также максимальное качество путешествия с таким временем.

Входные данные

В первой строке входных данных заданы два целых числа (2 ≤ n ≤ 106, 1 ≤ m ≤ 106) — количество городов и количество маршрутов соответственно.

Далее в m строках содержится описание маршрутов.

Описание каждого маршрута начинается с целого числа si  — количество перегонов в маршруте с номером i (1 ≤ si ≤ 106). Далее следуют (2si + 1) целых чисел, описывающих города маршрута и время проезда перегона между соседними городами маршрута, в следующем порядке: vi, 1, ti, 1, vi, 2, ti, 2, vi, 3, ..., ti, si, vi, si + 1, где vi, j — номер j-го города маршрута, ti, j — время проезда перегона между j-м и (j + 1)-м городом (1 ≤ vi, j ≤ n, 1 ≤ ti, j ≤ 1000).

Гарантируется, что s1 + s2 + ... + sm ≤ 106. Никакие два города в описании маршрута не совпадают. Гарантируется, что с помощью имеющихся маршрутов можно добраться из города с номером 1 в город с номером n.

Выходные данные

Выходные данные должны содержать два целых числа — минимальное суммарное время, которое придется провести в поездах, и максимальное качество пути с таким временем.

Примечание

В первом примере группа туристов отправится прямым маршрутом в Метрополис.

Во втором примере не оптимально проехать напрямую по первому маршруту, так как время в поезде при этом не будет минимальным возможным. Поэтому они отправятся на поезде по маршруту 1 из города 1 в город 2, затем на поезде по маршруту 2 из города 2 в город 3, а затем снова на поезде по маршруту 1 из города 3 в город 5. При этом сумма квадратов промежутков времени, проведенных в поездах между пересадками, равна 32 + 12 + 52 = 35.

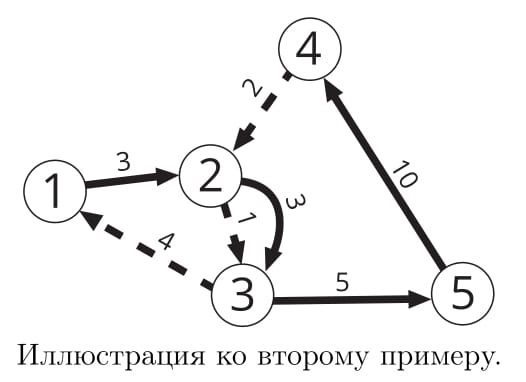
В третьем примере добраться из города 1 в город 4 за минимальное время можно, пересаживаясь с маршрута 1 на маршрут 2 в любом из городов 2, 3 или 4. Максимальное качество путешествия достигается при пересадке в городе 2: 12 + 92 = 82.

Обратите внимание, что второй и третий примеры не удовлетворяют ограничениям первой и второй подзадачи, решение будет протестировано на этих подзадачах, если оно пройдет первый тест из примера. Все тесты из примера подходят под ограничения подзадач 3 – 7, решение будет проверяться на тестах этих подзадач только в случае прохождения всех тестов из примера.

Примеры
Входные данные
2 1
1 1 3 2
Выходные данные
3 9
Входные данные
5 2
4 1 3 2 3 3 5 5 10 4
3 4 2 2 1 3 4 1
Выходные данные
9 35
Входные данные
5 2
3 1 1 2 2 3 3 4
3 2 2 3 3 4 4 5
Выходные данные
10 82
#113935
Лабиринт
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

В одном из уровней компьютерной игры вы попали в лабиринт, состоящий из n строк, каждая из которых содержит m клеток. Каждая клетка либо свободна, либо занята препятствием. Стартовая клетка находится в строке r и столбце c . За один шаг вы можете переместиться на одну клетку вверх, влево, вниз или вправо, если она не занята препятствием. Вы не можете перемещаться за границы лабиринта.

К сожалению, ваша клавиатура крайне близка к поломке, поэтому вы можете переместиться влево не более x раз и вправо не более y раз. При этом ограничений на перемещения вверх и вниз нет, поскольку клавиши, используемые для движения вверх и вниз, всё ещё в идеальном состоянии.

Теперь вы для каждой клетки поля решили установить, можно ли выбрать такую последовательность нажатий, которая приведёт вас из стартовой в эту клетку. Посчитайте, сколько клеток поля обладают таким свойством.

Входные данные

Первая строка содержит два целых числа n , m ( 1 ≤ n , m ≤ 2000 ) — количество строк и столбцов в лабиринте, соответственно.

Вторая строка содержит два целых числа r , c ( 1 ≤ r ≤ n , 1 ≤ c ≤ m ) — номер строки и столбца, на пересечении которых расположена стартовая клетка.

Третья строка содержит два целых числа x , y ( 0 ≤ x , y ≤ 10 9 ) — максимальное количество перемещений влево и вправо, соответственно.

Следующие n строк содержат описание лабиринта. Каждая из этих строк имеет длину m и состоит только из символов ' . ' и ' * '. В i -й строке j -й символ соответствует клетке лабиринта с номерами строки и столбца i и j , соответственно. Символ ' . ' соответствует свободной клетке лабиринта, а символ ' * ' — клетке с препятствием.

Гарантируется, что стартовая клетка не занята препятствием.

Выходные данные

Выведите одно число — количество клеток лабиринта, достижимых из стартовой, включая её саму.

Примечание

Клетки, достижимые в соответствующем примере, отмечены ' + '.

Первый пример 


+++..
+***.
+++**
*+++.

Второй пример 


.++.
.+*.
.++.
.++.
Примеры
Входные данные
4 5
3 2
1 2
.....
.***.
...**
*....
Выходные данные
10
Входные данные
4 4
2 2
0 1
....
..*.
....
....
Выходные данные
7
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест