Темы --> Информатика --> Алгоритмы --> Алгоритмы сортировки
    Квадратичные сортировки(24 задач)
    Сортировка записей(9 задач)
    Использование сортировки(13 задач)
    Быстрая сортировка(55 задач)
    Сортировка слиянием(9 задач)
    Сортировка подсчетом(27 задач)
    Сканирующая прямая(39 задач)
    Сортировка событий(4 задач)
---> 194 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 32 33 34 35 36 37 38 >> Отображать по:
#112125
Коррозия металла
  
ограничение по времени на тест
0.25 second;
ограничение по памяти на тест
256 megabytes

Для хранения двух агрессивных жидкостей \(A\) и \(B\) используется емкость с многослойной перегородкой, которая изготавливается из имеющихся \(N\) листов. Для каждого листа \(i\) (\(i\) = 1, ..., \(N\)) известно время его растворения жидкостью \(A\) - \(a_i\) и жидкостью \(B\) - \(b_i\). Растворение перегородки каждой из жидкостей происходит последовательно лист за листом, с постоянной скоростью по толщине листа. Требуется спроектировать такую перегородку, время растворения которой было бы максимальным.

В первой строке входного файла записано число \(N\) (1 ≤ \(N\) ≤ 256). В каждой из последующих N строк содержатся два положительных вещественных числа \(a_i\) и \(b_i\), разделенные пробелом.

Выходные данные

В первую строку выходного файла записать время растворения перегородки с точностью до 3 цифр после десятичной точки. В следующую строку файла записать номера листов в порядке их расположения от жидкости A к жидкости B, разделяя числа пробелами.

Примеры
Входные данные
4
1 2
1 2
0.5 1.5
7 3.5
Выходные данные
6.00000000
4 2 1 3
#112519
Артемида
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Зевс подарил Артемиде, богине охоты, прямоугольный участок земли, чтобы вырастить лес. Левая сторона этого участка  — это отрезок неотрицательного луча оси ординат, нижняя сторона — отрезок неотрицательного луча оси абсцисс, а (0, 0) — левый нижний угол участка. Зевс сказал Артемиде выращивать деревья только в точках с целыми координатами.

Артемида любит, когда лес выглядит естественно, и поэтому в её лесу любая прямая, проходящая через два дерева, не параллельна ни оси абсцисс, ни оси ординат.

Иногда Зевс хочет, чтобы Артемида вырубила для него деревья. Деревья должны быть вырублены так, чтобы выполнялись следующие условия:

  1. Зевс хочет, чтобы для него было вырублено хотя бы T деревьев.
  2. Чтобы потом построить прямоугольное футбольное поле для будущих футбольных успехов, Артемида должна вырубить все деревья внутри и на границе некоторой прямоугольной площадки, и ни одно дерево вне этой площадки.
  3. Стороны этой площадки должны быть параллельны осям координат.
  4. В двух противоположных углах площадки должны быть расположены деревья (которые будут вырублены).

Так как Артемида любит деревья, она хочет выполнить все условия таким образом, чтобы пришлось вырубить как можно меньше деревьев. Напишите программу, которая по информации о лесе и минимальному количеству деревьев T , которые должны быть вырублены, выбирает площадку, на которой Артемида будет вырубать деревья.

Входные данные

Первая строка ввода содержит единственное число N — количество деревьев в лесу ( 1 < N ≤ 20 000 ). Вторая строка содержит единственное число T — минимальное количество деревьев, которые должны быть вырублены ( 1 < T ≤ N ). Следующие N строк описывают расположение деревьев. Каждая из этих строк содержит по два целых числа X и Y — координаты дерева ( 0 ≤ X , Y ≤ 64 000 ). Решения, работающие только для N < 5000 , будут оцениваться из 50 баллов.

Выходные данные

Вывод должен содержать единственную строку, в которой записано два целых числа I и J , разделённых пробелом: Артемида должна вырубить деревья на площадке, углами которой будут деревья с номерами I и J (это те деревья, которые описаны в строках входного файла с номерами I + 2 и J + 2 ). Эти числа можно выводить в любом порядке. Возможно, есть несколько способов выбрать эти деревья, и в этом случае вы должны вывести любую из подходящих пар. Гарантируется, что во всех тестах жюри существует хотя бы одно решение.

Примеры
Входные данные
3
2
1 1
2 3
5 6
Выходные данные
1 2
#112533
Поразрядная сортировка
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Поразрядная сортировка является одним из видов сортировки, которые работают за линейное от размера сортируемого массива время. Такая скорость достигается за счет того, что эта сортировка использует внутреннюю структуру сортируемых объектов. Изначально этот алгоритм использовался для сортировки перфокарт. Первая его компьютерная реализация была создана в университете MIT Гарольдом Сьюардом (Harold Н. Seward). Опишем алгоритм подробнее. Пусть задан массив строк s 1 , ..., s i причем все строки имеют одинаковую длину m . Работа алгоритма состоит из m фаз. На i -ой фазе строки сортируются па i -ой с конца букве. Происходит это следующим образом. Будем, для простоты, в этой задаче рассматривать строки из цифр от 0 до 9. Для каждой цифры создается «корзина» («bucket»), после чего строки s i распределяются по «корзинам» в соответствии с i -ой с конца цифрой. Строки, у которых i -ая с конца цифра равна j попадают в j -ую корзину (например, строка 123 на первой фазе попадет в третью корзину, на второй — во вторую, на третьей — в первую). После этого элементы извлекаются из корзин в порядке увеличения номера корзины. Таким образом, после первой фазы строки отсортированы по последней цифре, после двух фаз - по двум последним, ..., после m фаз - по всем. При важно, чтобы элементы в корзинах сохраняли тот же порядок, что и в исходном массиве (до начала этой фазы). Например, если массив до первой фазы имеет вид: 111,112,211, 311, то элементы по корзинам распределятся следующим образом: в первой корзине будет. 111,211,311, а второй: 112. Ваша задача состоит в написании программы, детально показывающей работу этого алгоритма на заданном массиве.

Входные данные

Первая строка входного файла содержит целое число n (1 ≤ n ≤ 1000) . Последующие n строк содержат каждая по одной строке s i . Длины всех s i , одинаковы и не превосходят 20. Все s i состоят только из цифр от 0 до 9.

Выходные данные

В выходной файл выведите исходный массив строк в, состояние «корзин» после распределения элементов по ним для каждой фазы и отсортированный массив. Следуйте формату, приведенному в примере.

Примеры
Входные данные
9
12
32
45
67
98
29
61
35
09
Выходные данные
Initial array:
12, 32, 45, 67, 98, 29, 61, 35, 09
**********
Phase 1
Bucket 0: empty
Bucket 1: 61
Bucket 2: 12, 32
Bucket 3: empty
Bucket 4: empty
Bucket 5: 45, 35
Bucket 6: empty
Bucket 7: 67
Bucket 8: 98
Bucket 9: 29, 09
**********
Phase 2
Bucket 0: 09
Bucket 1: 12
Bucket 2: 29
Bucket 3: 32, 35
Bucket 4: 45
Bucket 5: empty
Bucket 6: 61, 67
Bucket 7: empty
Bucket 8: empty
Bucket 9: 98
**********
Sorted array:
09, 12, 29, 32, 35, 45, 61, 67, 98
#112542
Точки и отрезки
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
64 megabytes

Дано n отрезков на числовой прямой и m точек на этой же прямой. Для каждой из данных точек определите, скольким отрезкам они принадлежат. Точка x считается принадлежащей отрезку с концами a и b , если выполняется двойное неравенство min ( a , b ) ≤ x ≤ max ( a , b ) .

Входные данные

Первая строка содержит два целых числа n (1 ≤ n ≤ 10 5 ) – число отрезков и m (1 ≤ m ≤ 10 5 ) – число точек. В следующих n строках по два целых числи a i и b i – координаты концов соответствующего отрезка(например, может быть пара 5 2). В последней строке m целых чисел – координаты точек. Все числа по модулю не превосходят 10 9

Выходные данные

В выходной файл выведите m чисел – для каждой точки количество отрезков, в которых она содержится.

Примеры
Входные данные
3 2
0 5
-3 2
7 10
1 6
Выходные данные
2 0
Входные данные
1 3
-10 10
-100 100 0
Выходные данные
0 0 1
#112550
Интервалы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

В подвале вновь построенного здания на потолке расположен сильный источник света. К сожалению, покрытие на полу очень чувствительно к свету и разрушается под его воздействием. Чтобы этого избежать было решено защитить покрытие от света, однако сделать это не легко, т.к. в подвале проходит много труб и если они уже загораживают часть пола от света, то соответствующие участки было решено дополнительно не защищать.

Поиск решения можно проводить с помощью двухмерной модели. В этой модели ось Ох расположена на уровне пола, источник света считается точкой с целочисленными координатами ( b x , b y ) . Трубы представляют собой окружности. Центр i -й окружности имеет целочисленные координаты ( с x , c y ) , радиус r i также целый. Так как трубы сделаны из твердого материала, окружности не пересекаются. Трубы не отражают и не пропускают свет. Вы должны написать программу, которая найдет непересекающиеся интервалы на оси Ох , которые уже защищены от света благодаря имеющимся трубам.

Входные данные

Входной файл состоит из набора сразу нескольких тестов. Общее число строк в файле не превосходит 20000 . В первой строке каждого теста содержится положительное целое число N ≤ 10000 — обозначающее количество труб. Во второй строке расположены два целых числа b x и b y , разделенных пробелом. Каждая из следующих N строк содержит 3 целых числа через пробел с x , c y и r i , причем c y + r i < b y . Последний тест содержит единственную строку, содержащую N = 0 .

Выходные данные

Для каждого теста выведите набор искомых интервалов по одному в строке. Интервал описывается двумя вещественными координатами. Ответ будет считаться правильным, если его относительная и абсолютная погрешности не будут превосходить \(10^{-6}\). Интервалы должны быть отсортированы в порядке возрастания координаты x . В конце каждого набора интервалов выводите пустую строчку.

Примечание

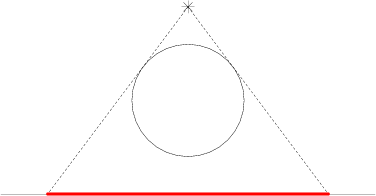
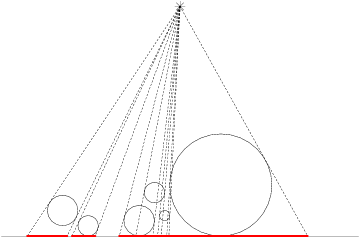
Картинки иллюстрируют тест из условия.

Примеры
Входные данные
1
300 300
300 150 90
6
300 450
70 50 30
120 20 20
270 40 10
250 85 20
220 30 30
380 100 100
0
Выходные данные
75.00 525.00

0.72 78.86
88.50 133.94
181.04 549.93
Страница: << 32 33 34 35 36 37 38 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест