Сортировка записей(9 задач)
Использование сортировки(13 задач)
Быстрая сортировка(55 задач)
Сортировка слиянием(9 задач)
Сортировка подсчетом(27 задач)
Сканирующая прямая(39 задач)
Сортировка событий(4 задач)
Королевские Железные Дороги (КЖД) готовятся открыть новый, скоростной, маршрут из столицы в соседний город NN и обратно. Новые поезда будут добираться до места назначения втрое быстрее обычных ночных поездов. Конкурс на поставку новых составов выиграла зарубежная компания «MacroHard» — производитель локомотивов «Hawk», которые будут использоваться в королевстве под локализованным названием «Ястреб». Расписание уже готово, но до сих пор не решен вопрос, сколько именно составов нужно, чтобы его выполнить. Не требуется покупать по составу на каждый рейс, поскольку поезд, прибывший на станцию, может выполнить и обратный рейс. КЖД обратились к вам и просят написать программу, способную рассчитать минимально необходимое количество поездов на один день. Расписание состоит из N 1 рейсов из столицы в город NN и N 2 обратных рейсов. Для каждого рейса известно время отправления и время прибытия — с точностью до минуты. Любой рейс полностью выполняется в течение одних календарных суток (с 00: 00 до 23: 59 включительно) — то есть никакой рейс не прибывает на следующий день после отправления. Каждый рейс занимает как минимум одну минуту, то есть ни один поезд не прибывает на станцию назначения в ту же минуту, в которую он отправился . КЖД настолько эффективны, что после прибытия поезд готов в ту же минуту отправиться в обратный рейс. Одновременно на станции может находиться, отправляться или прибывать любое количество поездов. Руководство КЖД не одобряет холостые поездки, поэтому поезда не могут перемещаться вне расписания в течение дня. Отметим, что вам не нужно учитывать подготовку к выполнению расписания следующего дня — к моменту начала следующих суток железнодорожники способны обеспечить любое распределение составов по станциям, независимо от того, как они были распределены к концу предыдущих.
В первой строке находится число N 1 (1 ≤ N 1 ≤ 100000) — количество рейсов из столицы в город NN. В следующих N 1 строках находятся описания рейсов, по одному на строке: время прибытия и время отправления, разделенные дефисом («-»). И время прибытия, и время отправления записаны в формате HH : MM ,где HH — час (число от 0 до 23, при необходимости, дополненное ведущим нулем до двух цифр), MM — минута (число от 0 до 59, при необходимости, дополненное ведущим нулем до двух цифр). В N 1 + 2 - й строке находится число N 2 (1 ≤ N 2 ≤ 100000) — количество обратных рейсов: из города NN в столицу. На следующих N 2 строках находятся описания этих рейсов в том же формате.
Выведите единственное число — минимально возможное количество составов, которое нужно для выполнения расписания.
В первом примере семь поездов могут выполнить рейсы, например, следующим образом: 1. обратно 6:35, туда 19:00
2. туда 6:45, обратно 11:00
3. обратно 7:15, туда 20:08
4. туда 7:36, обратно 15:40
5. обратно 14:00
6. обратно 18:35
7. обратно 20:20.
Во втором примере один поезд может выполнить все рейсы.
4 06:45-10:20 07:36-11:26 19:00-22:35 20:08-23:58 7 06:35-10:10 07:15-11:10 11:00-14:48 14:00-17:48 15:40-19:28 18:35-22:23 20:20-23:55
7
2 10:00-12:00 15:00-17:00 2 12:30-14:30 17:30-19:30
1
В далекой стране есть N городов. Был избран новый премьер-министр. В настоящее время в этой стране нет ни одной дороги, поэтому премьер-министр решил модернизировать страну, соединив некоторые города с двусторонними автострадами в транспортные сети. Два города будут расположены в одной и той же сети, если можно добраться до одного города от другого, используя недавно построенные дороги. Каждый город будет расположен в какой-то сети. Каждая сеть состоит из одного или нескольких городов.
Города представлены в виде точек в двумерной системе координат. Дорога между двумя городами представлена в виде отрезка, соединяющего две точки, в которых расположены города. Длина дороги равна длине отрезка в километрах.
В настоящее время страна переживает экономический спад, поэтому премьер-министр решил, что из-за отсутствия бюджета они не будут строить дороги длиннее, чем D километров. Кроме того, премьер-министр радуется мелочам, поэтому он будет счастлив, если по крайней мере в одной сети будет существовать непустое подмножество городов (оно может включать все города в сети), где общая сумма жителей делится на К . Например, если K = 4 и есть сеть с городами, в которых есть 3 , 5 , 7 жителей соответственно, премьер-министр будет счастлив, потому что сумма жителей в первых двух городах равна 8 .
Помогите премьер-министру сократить расходы, определив минимальный уровень D , необходимый для того чтобы премьер-министр мог строить дороги и одновременно быть счастливым.
Первая строка ввода содержит целые числа N и K (1 ≤ N ≤ 50000, 1 ≤ K ≤ 30) . Каждая из следующих N строк содержит три целых числа x i ; y i ; k i (0 ≤ x i , y i , k i ≤ 100000000) , которые представляют координату x города, координату y и количество жителей в этом городе, соответственно. На входных данных не будет двух городов с одинаковыми координатами. Кроме того, не будет ни одного города, в котором число жителей делится на К .
Первая и единственная строка вывода должна содержать минимальную D с точностью до 3 -х знаков после запятой, такую, что можно строить дороги с условием, что премьер-министр будет счастлив. Входные данные будут такими, чтобы всегда было решение.
Объяснение первого примера: единственный способ удержать премьер-министра в счастливом настроение - все города должны находятся в одном округе. Минимальный D , для которого это возможно, равен 1.414 .
Объяснение второго примера: премьер-министр будет рад, если первые 5 городов находятся в одном округе. Если D = 5.657 , премьер-министр может соединить города 1, 2, 3, 5 с городом 4 . В этом случае сумма жителей в городах 1, 2, 3, 4, 5 составит 11 , что делится на 11 , Поэтому премьер-министр будет счастлив.
3 3 0 4 4 1 5 1 2 6 1
1.414
6 11 0 0 1 0 1 2 1 0 3 1 1 4 5 5 1 20 20 10
5.657
6 5 20 20 9 0 0 3 0 1 1 10 0 1 10 1 6 12 0 3
2.000
Компания « Rapid City Dynamics » знаменита её роботами-собаками, роботами-гепардами и даже человекоподобными роботами. Но большие проекты требуют больших денег, так что компания решила создать что-то простое, но популярное (и более востребованное). Так что компания разрабатывает нового робота « Rat-O-Matic », и вы, как работник « Rapid City Dynamics », принимаете участие в этом.
Робот выглядит как механическая крыса, которая может двигаться и генерировать мелодию, наступая на специальные рамки. Плоскость бесконечна во все стороны, и на ней задана декартова система координат.
Есть ровно n рамок. Каждая рамка задана тремя числами: x , y и r . Она задаёт территорию, ограниченую между двух квадратов со сторонами параллельным осям координат и центрами в точке ( x , y ): радиус первого квадрата r , а второго — 2· r . Радиус квадрата — это расстояние между его центром и стороной. Ко всему прочему, каждой рамке соответствует своя нота. Сейчас есть только 3 возможных ноты, обозначим их как « r », « a » и « t ».
Гарантируется, что никакие две рамки не касаются и не пересекаются.
Вы можете взаимодействовать с роботом, вбивая номер рамки на специальной клавиатуре (рамки пронумерованы начиная с 1 ). Изначально, крыса находится снаружи всех рамок. Благодаря патентованной системе навигации, робот выбирает путь до рамки, который пересекает минимальное количество рамок. Когда крыса наступает на рамку в первый раз, соответствующая нота добавляется в мелодию. Робот останавливается после того, как наступит на нужную рамку.
Известно, что людям нравятся похожие мелодии. В вашей базе данных имеются m мелодий. Каждая мелодия задаётся строкой из символов, которая задаёт ноты. Мелодия, сгенерированная крысой, содержится в мелодии из базы данных, если она содержится в ней в качестве подстроки. Популярность сгенерированной мелодии - это число мелодий в базе данных, которые содержат её. Одинаковые мелодии из базы данных должны быть учтены несколько раз.
В попытке создания самого классного расположения рамок, вы совершили q экспериментов. Эксперименты бывают трёх типов:
Твоя задача — провести эти эксперименты, используя только свой компьютер!
В первой строке содержится натуральное число n — количество рамок ( 1 ≤ n ≤ 2·10 5 ).
В следующих
n
строках описаны рамки,
i
-я из них содержит три натуральных числа
x
i
,
y
i
,
r
i
и символ
c
i
, разделённые пробелами (
- 10
8
≤
x
i
,
y
i
≤ 10
8
,
1 ≤
r
i
≤ 10
8
, и
c
i
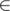 {«
r
», «
a
», «
t
»} — координаты центра рамки, радиус внутреннего квадрата и её нота, соответственно.
{«
r
», «
a
», «
t
»} — координаты центра рамки, радиус внутреннего квадрата и её нота, соответственно.
Следующая строка содержит натуральное число m — количество мелодий в базе ( 1 ≤ m ≤ 2·10 5 ).
Следующие m строк содержат непустые строки из букв « r », « a » или « t », которые задают мелодии. Суммарная длина всех строк не превосходит 2·10 5 .
Следующая строка содержит натуральное число q — количество экспериментов ( 1 ≤ q ≤ 2·10 5 ).
Следующие q строк описывают эксперименты, j -я из них содержит символ t j (« - », « + » или « ? ») и натуральное число x j отделённое пробелом. Символ задаёт тип эксперимента (« - » — 1, « + » — 2 и « ? » — 3), а число обозначает номер рамки.
Гарантируется, что есть хотя бы один эксперимент третьего типа.
Для каждого эксперимента третьего типа, выведите одно число — популярность получившейся мелодии.
10 баллов — (1 ≤ n, m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 2-6) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 7-9) .
10 баллов — ( 1 ≤ n, q ≤ 100, 1 ≤ m ≤ 200 000 , суммарная длина строк не превосходит 200 000, тесты 10-13) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m ≤ 200 000, 1 ≤ q ≤ 100, суммарная длина строк не превосходит 200 000, тесты 14-16) .
10 баллов — ( 1 ≤ n ≤ 200 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 17-19) .
15 баллов — ( 1 ≤ n, q ≤ 200 000, 1 ≤ m ≤ 100, суммарная длина строк не превосходит 100, тесты 20-23) .
35 баллов — полные ограничения, тесты 24-57.
3 3 3 4 r 2 4 1 a 14 4 1 t 3 rat rara aaa 6 ? 3 ? 2 - 1 ? 2 + 1 ? 2
1 2 3 2
Совсем скоро начнётся чемпионат Хорватии по хорватскому хоккею. В хорватском хоккее каждая игра длится по M минут и в каждый момент времени на поле находятся ровно 6 игроков. Так как игра может длиться очень долго, не все игроки могут находится на поле на протяжении всей игры. Поэтому каждая команда привезла на чемпионат большое число запасных игроков.
Сегодня мы будем помогать Анте, тренеру команды Загреба. Анте привёз N игроков на чемпионат, причём у каждого игрока есть своя сила p i и своя выносливость d i . Для каждого игрока известно, что его «суммарное игровое время» не превышает величину его выносливости. «Суммарное игровое время» игрока — это суммарное количество времени, которое игрок провёл на поле. То есть, если игрок сначала провёл на поле X минут, а потом Y минут, то его «суммарное игровое время» равно X + Y минут.
В каждой момент времени у команды есть её сила — сумма сил всех шестерых игроков, находящихся на поле. Общая сила команды Z — это сумма сил команды во все минуты игры. То есть, если игра длилась 3 минуты и в первую минуту сила команды была 15 , во вторую — 12 , а в третью — 14 , то общая сила команды — 15 + 12 + 14 = 41 . Анте знает, что чтобы победить, надо максимизировать общую силу команды. Но Анте — не очень талантливый тренер, поэтому он просит вас помочь ему составить оптимальное расписание выхода команд, чтобы Z было максимально. Гарантируестя, что можно составить расписание так, чтобы в каждый момент на поле было по 6 игроков.
Обратите внимание, что в хорватском хоккее все игроки могут заменять друг друга, и вратаря нет, ведь так игра становиться гораздо веселее.
В первой строке вводится 2 числа M и N ( 1 ≤ M ≤ 5·10 5 , 6 ≤ N ≤ 5·10 5 ) — длительность матча в минутах и число игроков у команды соответственно.
В каждой из следующих N строк даны по 2 числа p i и d i ( 1 ≤ p i ≤ 10 5 , 1 ≤ d i ≤ M ) — сила и выносливость i -го игрока.
Все игроки пронумерованы от 1 до N в порядке, данном во входных данных.
В первой строке выведите Z — максимальную возможную общую силу команды.
Во второй строке выведите 6 чисел — номера игроков, которые должны выйти на поле с самого начала.
В третей строке выведите B — число замен. Обратите внимание, что число замен не должно превосходить 3· N .
В следующих B строках выведите по 3 числа X , Y , Z ( 1 ≤ X < M , 1 ≤ Y , Z ≤ N ), описывающие замену игрока Y на игрока Z в момент времени X . Обратите внимание, что можно проводить несколько замен в один момент времени, но не допускается выход в игру на нулевое время (т.е. выход в игру и замена в один момент времени или наоборот).
Если существует несколько ответов, выведите любой.
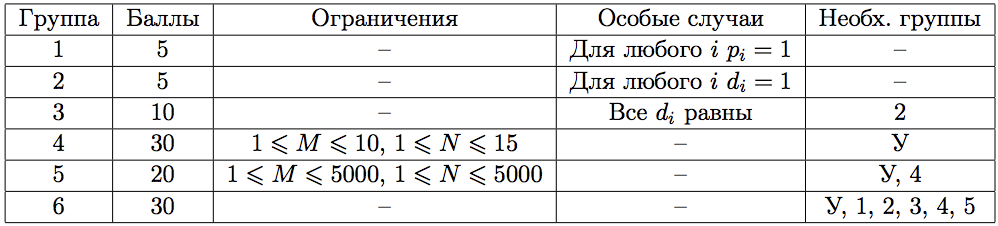
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, что прохождение тестов из условия (обозначается «У») не всегда обязательно для принятия на проверку.
200 6 3 200 4 200 5 200 6 200 7 200 8 200
6600 6 5 4 3 2 1 0
9 9 10 3 9 3 13 9 5 3 15 9 100 9 3 6 2 6 1 6
1260 6 5 3 1 7 8 4 3 8 9 3 1 2 6 7 8 6 2 4
3 9 100 3 100 3 100 3 100 3 100 2 100 1 50 1 30 2 1 1
1610 1 2 3 4 5 7 2 1 7 8 2 5 6
В один прекрасный день маленький Дональд решил вымыть N своих чистых белых простыней. После мытья он положил их на землю во дворе, чтобы их высушить. Дональд помещал простыни так, чтобы никакие две простыни не касались ни сторонами, ни углами, и чтобы их стороны не пересекалась, но возможно, что он разместил меньшие простыни поверх более крупных или что простыня полностью закрывает какие-то другие простыни. Сделав это, Дональд лег спать.
Друг Дональда Ким как-то узнал о том, что Дональд сушит простыни и решил пообщаться с ним. Он нашел пейнтбольный пистолет своего отца на чердаке. Наряду с пистолетом у него было несколько пейнтбольных мячей, каждый из них имел свой цвет (не обязательно уникальный). Как только Дональд заснул, Ким вошёл во двор к Дональду и начал стрелять пр простыням из пейнтбольного пистолета. Простыни Дональда очень тонкие, поэтому, когда Ким попадает в какую-то простыню, она пропускает краску дальше, на простыню ниже (и та тоже, и так происходит, пока не закончатся простыни и краска не попадет на землю). После того, как Ким использовал все шары, он с радостью покинул двор Дональда. Дональд был очень расстроен, увидев, что случилось с его простынями. Дональд очень заинтересован в правильных данных о преступлении Кима, но он в шоке и не способен думать, поэтому просит вас сказать ему количество цветов на каждой простыне.
Мы можем представлять двор Дональда как бесконечную систему координат, а простыни - как прямоугольники, параллельные осям координат. Выстрелы Кима могут быть представлены как точки в этой системе.
Когда-то в детстве дедушка рассказал Киму, что снаряд никогда не попадает в одну воронку дважды, так что координаты всех выстрелов попарно различны.
Первая строка ввода содержит два числа - количество простынь N ( 1 ≤ N ≤ 80000 ), и количество шаров M ( 1 ≤ M ≤ 80 000 ).
i -я из следующих N строк содержит четыре числа: координаты нижнего левого угла A i , B i ( 1 ≤ A i , B i ≤ 10 9 ) и верхнего правого угла C i , D i , ( 1 ≤ C i , D i ≤ 10 9 ) i -й простыни.
j -я из следующих M строк содержит три числа, где X j , Y j ( 1 ≤ X j , Y j ≤ 10 9 ) - координаты j -го выстрела Кима и K j ( 1 ≤ K j ≤ 10 9 ) - цвет j -го пейнтбольного шара.
i -я из N выходных строк должна содержать количество цветов на i -м листе.
Тесты к данной задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп.

2 2 1 1 3 3 5 6 10 10 3 3 1 5 1 2
1 0
3 3 1 1 7 7 2 2 6 6 3 3 5 5 4 4 1 2 6 2 4 7 3
3 2 1
1 3 1 1 7 7 2 6 2 4 7 3 4 4 1
3