Массивы(232 задач)
Типы данных(356 задач)
Циклы(177 задач)
Условный оператор (if)(164 задач)
Python(260 задач)
Standard Template Library(2 задач)
Строка s называется супрефиксом для строки t, если t начинается с s и заканчивается на s. Например, «abra» является супрефиксом для строки «abracadabra». В частности, сама строка t является своим супрефиксом. Супрефиксы играют важную роль в различных алгоритмах на строках.
В этой задаче требуется решить обратную задачу о поиске супрефикса, которая заключается в следующем. Задан словарь, содержащий n слов t1, t2, …, tn и набор из m строк-образцов s1, s2, …, sm. Необходимо для каждой строки-образца из заданного набора найти количество слов в словаре, для которых эта строка-образец является супрефиксом.
Требуется написать программу, которая по заданному числу n, n словам словаря t1, t2, …, tn, заданному числу m и m строкам-образцам s1, s2, …, sm вычислит для каждой строки-образца количество слов из словаря, для которых эта строка-образец является супрефиксом.
Первая строка входного файла содержит целое число n (1 ≤ n ≤ 200 000).
Последующие n строк содержат слова t1, t2, …, tn, по одному слову в каждой строке. Каждое слово состоит из строчных букв латинского алфавита. Длина каждого слова не превышает 50. Суммарная длина всех слов не превышает 106. Словарь не содержит пустых слов.
Затем следует строка, содержащая целое число m (1 ≤ m ≤ 200 000).
Последующие m строк содержат строки-образцы s1, s2, …, sm, по одной на каждой строке. Каждая строка-образец состоит из строчных букв латинского алфавита: Длина каждой строки-образца не превышает 50. Суммарная длина всех строк-образцов не превышает 106. Никакая строка-образец не является пустой строкой.
Выходной файл должен содержать m чисел, по одному на строке.
Для каждой строки-образца в порядке, в котором они заданы во входном файле, следует вывести количество слов словаря, для которых она является супрефиксом.
Решения, работающие при \(n\), \(m\) не превосходящими 100 оцениваются из 30 баллов.
4 abacaba abracadabra aa abra 3 a abra abac
4 2 0
Отправившись в заброшенные руины старого замка, герой нашел в подземелье сундук, наполненный сокровищами. Особенно ему понравился меч из валирийской стали, с рукоятью, украшенной изумрудами.
Все свои вещи герой носит в рюкзаке. Единственное ограничение на содержимое рюкзака — чтобы вес его содержимого не превышал s единиц. У героя в рюкзаке уже лежит n предметов, причем i-й весит wi единиц. Меч весит m единиц.
Определите, сможет ли герой взять с собой меч, не выкидывая ничего из рюкзака.
Дано число s — максимальный вес, который можно поместить в рюкзак. Далее дано число n — количество вещей у героя в рюкзаке. В следующей строчке перечислены n чисел — веса всех предметов, лежащих в рюкзаке. В последней строчке записано число m — вес меча.
Выведите "YES", если герой сможет унести меч, и "NO", если не сможет (без кавычек).
10 3 2 1 4 3
YES
10 3 2 1 3 10
NO
Фирма, в которой всё ещё работает ваш друг, решила установить в своих маршрутках автоматы по продаже чая и кофе, чтобы во время поездок и, особенно, во время ожидания в пробках, пассажиры могли с толком провести время.
Стоимость стакана чая и кофе в автомате предполагается установить равной пяти рублям. Автоматы будут принимать монеты по 5 и 10 рублей, а также купюры в 10, 50 и 100 рублей. Когда пассажиру надо выдавать сдачу (т.е. когда пассажир бросил в автомат десятирублёвую монету или 10-, 50- или 100-рублёвую купюру), автомат выдаёт сдачу пятирублёвыми монетами; если же пассажир бросил в автомат пятирублёвую монету, то автомат её сохраняет и может использовать для сдачи следующим пассажирам.
Ясно, что, чтобы обеспечить возможность выдачи сдачи всем покупателям, может потребоваться изначально загрузить в автомат некоторое количество пятирублёвых монет. Сейчас на маршрутках фирмы проходят испытания с целью определить минимальное количество монет, которые надо загрузить в автомат перед выездом маршрутки в рейс. Вам дан протокол одного из таких испытаний: известен порядок, в котором пассажиры оплачивали свои покупки различными монетами и купюрами. Определите, какое минимальное количество пятирублёвых монет должно было изначально находиться в автомате, чтобы всем пассажирам хватило сдачи.
В первой строке входного файла находится одно натуральное число \(N\) — количество покупок в автомате, которые были совершены в ходе испытания (\(1\leq N\leq 50\,000\)). Во второй строке находятся \(N\) натуральных чисел, каждое из которых равно номиналу монеты или купюры, которую использовал очередной покупатель для оплаты; каждый номинал может принимать одно из четырёх значений: 5, 10, 50 или 100.
В выходной файл выведите одно число — минимальное количество пятирублёвых монет, которые надо было загрузить в автомат изначально, чтобы всем покупателям хватило сдачи.
В первом примере одна пятирублёвая монета потребуется для сдачи первому покупателю и 19 монет — третьему, но при сдаче третьему можно будет использовать ту монету, которую бросит второй покупатель, поэтому изначально в автомате достаточно 19 монет.
Во втором примере сдачу третьему покупателю можно выдать, используя монету первого или второго покупателя, и поэтому не требуется загружать монеты в автомат изначально.
В третьем примере первому же покупателю требуются девять монет сдачи, и все они должны изначально находится в автомате.
3 10 5 100
19
3 5 5 10
0
4 50 5 5 5
9
 Фирма, в которой работает ваш друг, решила установить на конечной остановке своих маршруток
большую абстрактную скульптуру со своим логотипом. Скульптура будет представлять собой
прямоугольную сетку из \(N\) строк и \(M\) столбцов, в некоторых узлах которой будут располагаться разноцветные шары.
Для обеспечения жёсткости конструкции шары, расположенные в узлах, соседних по вертикали,
горизонтали или диагонали, необходимо соединить металлическими стержнями. Более строго, два шара
должны быть соединены стержнем, если разность номеров строк, в которых расположены эти шары, не
превосходит по модулю единицы, и разность номеров столбцов тоже не превосходит по модулю единицы.
Фирма, в которой работает ваш друг, решила установить на конечной остановке своих маршруток
большую абстрактную скульптуру со своим логотипом. Скульптура будет представлять собой
прямоугольную сетку из \(N\) строк и \(M\) столбцов, в некоторых узлах которой будут располагаться разноцветные шары.
Для обеспечения жёсткости конструкции шары, расположенные в узлах, соседних по вертикали,
горизонтали или диагонали, необходимо соединить металлическими стержнями. Более строго, два шара
должны быть соединены стержнем, если разность номеров строк, в которых расположены эти шары, не
превосходит по модулю единицы, и разность номеров столбцов тоже не превосходит по модулю единицы.
Напишите программу, которая по заданному расположению шаров позволит определить, как будет выглядеть скульптура после установки стержней.
В первой строке входного файла находятся два натуральных числа \(N\) и \(M\) — размеры конструкции (\(1\leq
N,M\leq 100\)). Далее следуют \(N\) строк по \(M\) символов в каждой. Каждый символ — это или
“#” (решетка), обозначающий, что в соответствующем узле будет находиться шарик, или “.” (точка),
обозначающий, что соответствующий узел будет пустой.
Выведите в выходной файл \(2N-1\) строку по \(2M-1\) символов в каждой,
изображающие как сами шары, так и соединяющие их стержни. А именно,
в нечётных позициях нечётных строк выведите символ “#”
или “.”, в зависимости от того, заполнен этот узел шариком или нет,
а в остальных позициях выведите один из символов “ ” (пробел),
“-” (минус), “|” (вертикальная
палочка, ASCII #124),
“/” (дробь, ASCII #47), “\” (обратный слеш, ASCII #92) или “X”
(латинская заглавная буква X, ASCII #88), отражающий конфигурацию стержней в соответствующем месте структуры.
Если какая-то строка выходного файла должна заканчиваться на пробелы, их можно не выводить.
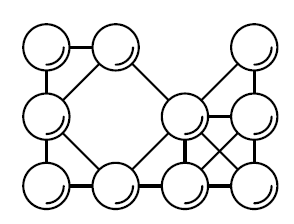
Первый пример соответствует рисунку.
3 4 ##.# #.## ####
#-# . # |/ \ /| # . #-# |\ /|X| #-#-#-#
3 4 .#.. #.#. .#..
. # . . / \ # . # . \ / . # . .
... но нужен ли на самом деле кому-нибудь 6\(1\over7\)-пунктовый шрифт, который на три четверти — шрифт Baskerville, и на четверть — Helvetica?
Дональд Э. Кнут. Идея Мета-фонта1
Маленькая девочка Оля добралась до полки, на которой стоят флаконы с мамиными любимыми духами, и начала заниматься своим любимым занятием — переливанием жидкостей из одного флакона в другой. Когда наконец мама застала её за этим занятием, прекрасная коллекция духов была уже безнадёжно утрачена.
К счастью, Оля — аккуратная девочка, поэтому все свои действия она записывала на бумажку. Помогите ей успокоить маму: определите, каков состав духов в первом (мамином любимом) флаконе, чтобы мама смогла придумать этой смеси новое название и рассказывать всем, какие прекрасные духи она смогла сделать вместе с дочерью.
Считайте, что Оля не пролила ни одной капли, а также что она тщательно встряхивала флаконы после каждого переливания. Учтите, что в маминых флаконах порой не видно, есть ли там жидкость, и потому Оля иногда могла пытаться переливать духи из пустого флакона (в результате, естественно, ничего не переливалось). Вы можете также считать, что после каждого переливания в каждом флаконе каждый тип духов либо полностью отсутствует, либо содержится в объеме не меньшем чем \(10^{-10}\).
На первой строке входного файла находятся два числа \(N\) и \(M\) — количество флаконов и число типов маминых любимых духов соответственно (\(2 \leq N \leq 100\); \(1 \leq M \leq 100\)). Далее следуют \(N\) строк, на \(i\)-ой из которых находятся два числа — тип \(L_i\) и объем \(V_i\) духов, находившихся изначально в \(i\)-ом флаконе (\(1\leq L_i \leq M\); \(0 \leq V_i \leq 1000\)). Возможно, что в нескольких флаконах находились духи одного и того же типа; возможно, что какого-то типа вообще не было на полке.
Далее во входном файле следует строка с числом \(K\) — количеством совершённых переливаний (\(1 \leq K \leq 1000\)). За ней следуют \(K\) строк, на \(k\)-ой из которых находятся три числа \(S_k\), \(T_k\) и \(A_k\) — номера флаконов, откуда и куда переливала Оля при \(k\)-ом переливании, и количество перелитой жидкости (в процентах от количества жидкости в \(S_k\)-ом флаконе перед переливанием). Гарантируется, что \(1\leq S_k,T_k\leq N\), что \(S_k\neq T_k\), и что \(0\leq A_k\leq 100\). Все числа во входном файле целые.
В выходной файл выведите \(M\) чисел — процентное содержание всех видов духов (от первого до \(M\)-ого) в первом флаконе после последнего переливания. Выводите результат с точностью не меньше двух знаков после запятой. Гарантируется, что после последнего переливания первый флакон оказался непустым.
1... but does anybody really need a 6\(1\over7\)-point font that is one fourth of the way between Baskerville and Helvetica? — Donald E. Knuth, The Concept of a Meta-Font
3 2 1 100 2 200 1 500 2 3 2 20 2 1 50
60.00 40.00