Темы --> Информатика --> Структуры данных
    Деревья(174 задач)
    Линейные структуры(59 задач)
    Корневая эвристика (sqrt декомпозиция)(14 задач)
    Разреженные таблицы (sparse table)(2 задач)
    Система непересекающихся множеств(16 задач)
    Хеш(35 задач)
    Персистентные структуры данных(2 задач)
---> 279 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 13 14 15 16 17 18 19 >> Отображать по:
#1376
Вес компоненты
  
ограничение по времени на тест
5.0 second;
ограничение по памяти на тест
256 megabytes

В неориентированный взвешенный граф добавляют ребра. Напишите программу, которая в некоторые моменты находит сумму весов ребер в компоненте связности.

Входные данные

В первой строке записано два числа n и m (1≤n,m≤106) - количество вершин в графе и количество производимых добавлений и запросов. Далее следует m строк с описанием добавления или запроса. Каждая строка состоит из двух или четырех чисел. Первое из чисел обозначает код операции. Если первое число 1, то за ним следует еще три числа x, y, w. Это означает, что в граф добавляется ребро из вершины x в вершину y веса w. (1≤x<y≤n, 1≤w≤103). Кратные ребра допустимы. Если первое число 2, то за ним следует ровно одно число x. Это означает, что необходимо ответить на вопрос, какова сумма ребер в компоненте связности, которой принадлежит вершина x (1≤x≤n).

Выходные данные

Для каждой операции с кодом 2 выведите ответ на поставленную задачу. Ответ на каждый запрос выводите на отдельной строке.

Примеры
Входные данные
6 10
2 1
1 1 2 1
2 1
1 2 4 2
2 1
1 1 4 3
2 1
1 3 5 3
2 5
2 6
Выходные данные
0
1
3
6
3
0
#1380
Умный чертежник
  
Линия задается набором вертикальных и горизонтальных отрезков единичной длины. Требуется изменить порядок отрезков так, чтобы линия не имела самопересечений (замена на самокасания).

Фирма "Макрохард" изобрела новое устройство с целью облегчить труд людей, кому по долгу службы приходится чертить много чертежей, а также школьников, изучающих черчение. Это устройство представляет собой крошечного робота, который умеет ползать по клетчатому листу бумаги. При этом в начале он обязательно должен быть расположен на пересечении линий сетки.

Этот робот умеет выполнять программу, которая может состоять из команд E,W,N,S — переместиться по листу в соседнюю вершину сетки вправо, влево, вперед, назад соответственно. Перемещаясь в соседний узел сетки, робот оставляет за собой ровную линию. При этом по правилам техники безопасности ему категорически запрещается проводить дважды одну и ту же линию, так как при попытке провести линию второй раз, он очень сильно пачкается в своих же собственных чернилах (они очень долго сохнут), и выходит из строя.

При этом, правда, через одну и ту же вершину сетки робот может проходить дважды. Возможно два случая (более толстой линией показано, как мы проезжаем через вершину в первый раз, более тонкой - во второй).

В первом случае мы оба раза проезжаем через вершину "прямо" (будем называть это самопересечением маршрута), а во втором случае — оба раза "поворачиваем" (это будем называть самокасанием).

Разработчики также установили, что в случае самопересечения маршрута робот пачкается в своих чернилах сильнее, чем в случае самокасания, и, если самопересечения встречаются часто, быстро выходит из строя. Поэтому они решили написать для него внутренний оптимизатор программы.

Вам дается программа для робота. Требуется изменить ее так, чтобы узор, получающийся в конце ее работы, был таким же, но при этом при работе робота не возникало самопересечений маршрута.

Входные данные

В первой строке входного файла содержится программа для робота. Таким образом, в первой строке входного файла могут встречаться только символы E,W,N,S, а также пробельные символы, которые должны игнорироваться. Общая длина строки (включая пробельные символы) не превышает 200 символов.

Выходные данные

В выходной файл вы должны вывести одну строку с оптимизированной программой. Эта строка должна удовлетворять тем же условиям, что и входная строка.

Примеры
Входные данные
EENWSSWNN
Выходные данные
ENESWSWNN
#1388
Сообщающиеся сосуды
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Сегодня на уроке физики рассказывали удивительные вещи. Придя домой, Витя решил проверить слова учителя о том, что если взять два одинаковых сосуда, соединенных тонкой трубкой на уровне основания, то уровень жидкости при любом ее количестве также будет одинаковым для обоих сосудов.

Способ убедиться в правильности утверждения Витя избрал довольно оригинальный. Он взял аквариум с основанием длиной N и шириной 1, очень высокими стенками, и поставил N –1 перегородку параллельно узкой боковой стенке аквариума, тем самым, разделив аквариум на N одинаковых отсеков. Каждая перегородка имеет ширину 1 и очень большую высоту. Толщиной перегородки можно пренебречь. В каждой из перегородок есть точечное отверстие на высоте Hi, диаметром которого также можно пренебречь. После всех этих приготовлений Витя медленно наливает в первый отсек (между стенкой и 1ой перегородкой) C литров воды. В часть аквариума размером 1x1x1 вмещается ровно один литр воды. Так как стенки и перегородки в аквариуме были очень высокими, то через край вода не переливалась. После установления стационарного состояния он замерил уровень жидкости в каждом из N сосудов.

Теперь он хочет убедиться, что его экспериментальные данные не опровергают законы, рассказанные на уроке. Он обратился к вам с просьбой выяснить, какой должна быть высота жидкости в каждом из сосудов с теоретической точки зрения.

Рассмотрим подробно случай N = 3. Пусть сначала H1 < H2. Как только жидкость в первом отсеке достигнет уровня первого отверстия, вода станет поступать во второй отсек до тех пор, пока уровни в обоих отсеках не сравняются (или уровень воды в первом отсеке окажется равным H1, тогда во втором отсеке он будет на уровне С – H1). Далее уровень жидкости в первых двух частях будет увеличиваться равномерно (или не будет меняться). Как только вода достигнет второго отверстия, вся она будет поступать в третий отсек, опять же до тех пор, пока уровни жидкости во всех трех частях не сравняются или вода в первых двух отсеках достигнет уровня H2. После этого, если воды оказалось достаточно, весь аквариум будет заполняться равномерно.

Пусть теперь H1 > H2. Как только жидкость в первом отсеке достигнет уровня первого отверстия, вся вода станет поступать во второй отсек. Если после этого уровень во втором отсеке сравняется с уровнем второго отверстия, то вода станет выливаться в третий до тех пор, пока высоты жидкостей во втором и третьем отсеках не станут равными. Далее уровень воды в них будет равномерно увеличиваться, пока не достигнет первого отверстия. После этого весь аквариум будет заполняться равномерно.

Входные данные

В первой строке записаны целые N и C (1 ≤ N ≤ 100000, 0 ≤ C ≤ 2*109). В следующих N –1 строках содержится по одному целому числу Hi (0 ≤ Hi ≤ 2*109), обозначающему высоту отверстия в i-й перегородке.

Выходные данные

Выведите N чисел, каждое на новой строке, с точностью до шести знаков после десятичной точки —уровень жидкости в 1, 2, ..., N отсеке соответственно.

Частичные ограничения

Первая группа состоит из тестов, в которых N ≤ 100. Оценивается в 30 баллов.

Вторая группа состоит из тестов, в которых N ≤ 10000. Оценивается в 30 баллов.

Примеры
Входные данные
4 4
3
2
1
Выходные данные
3.00000000000000000000
1.00000000000000000000
0.00000000000000000000
0.00000000000000000000
Входные данные
4 10
1
2
3
Выходные данные
3.00000000000000000000
3.00000000000000000000
3.00000000000000000000
0.99999999999999911000
#1390
Симпатичные прямоугольники
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Знаменитый художник Вася только что закончил работу над своим новым шедевром и хочет знать, сколько он сможет получить за свой труд.

Картина представляет собой прямоугольник N на M сантиметров, разделенный на маленькие квадратики 1 на 1 сантиметр со сторонами, параллельными сторонам картины. Для достижения гармонии каждый из этих квадратиков Вася покрасил одним из 26 особых цветов, обозначаемых маленькими латинскими буквами.

Стоимость картины в точности равна количеству «симпатичных» частей в ней. Частью картины называется любой прямоугольник, который может быть вырезан из нее по границам квадратиков. Часть называется «симпатичной», если при выполнении симметрии относительно ее центра получается прямоугольник, раскрашенный также, как и исходная часть. Например, в картине, раскрашенной так:

abc
acb

симпатичными являются все части, состоящие из одного квадратика (их 6), а также части

bc и a

cb и a

Напишите программу, которая по информации о шедевре Васи определит его стоимость.

Входные данные

В первой строке содержатся два числа N и M (1 ≤ N, M ≤ 100). В следующих N строках идут строки, состоящие из M маленьких латинских символов. Символ в i-й строке j-м столбце определяет цвет соответствующего квадратика картины.

Выходные данные

Выведите стоимость шедевра — количество частей, симметричных относительно своего центра.

Комментарии к примерам тестов

Этот пример разобран в условии

Симпатичными являются шесть частей 1x1, одна часть 1x2 и сама картина.

Частичные ограничения

Первая группа состоит из тестов, в которых N, M ≤ 15. Данная группа оценивается в 30 баллов.

Вторая группа состоит из тестов, в которых N, M ≤ 50. Данная группа оценивается в 30 баллов.

Примеры
Входные данные
2 3
abc
acb
Выходные данные
8
Входные данные
3 2
ab
cc
ba
Выходные данные
8
#1396
Эволюция
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

>Во время исследований, посвященных появлению жизни на планете Олимпия, учеными было сделано несколько сенсационных открытий:

  1. Все живые организмы планеты происходят от бактерии Bitozoria Programulis.
  2. Эволюция происходила шаг за шагом (по предположению ученых – во время изменения климата на планете).
  3. На каждом шаге эволюции из каждого вида образовывались ровно два подвида, а предыдущий вид исчезал.
  4. Если считать появление бактерии Bitozoria Programulis первым шагом эволюции, то существующие сейчас живые организмы находятся на N-ом шаге.

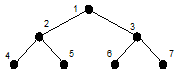
Чтобы не придумывать названия во время исследований, ученые пронумеровали все виды организмов, которые когда-либо существовали на планете. Для этого они нарисовали дерево эволюции с корнем Bitozoria Programulis, которая получила номер 1. Далее нумеровали виды каждого шага эволюции слева направо. Таким образом непосредственные подвиды Bitozoria Programulis получили номера 2 и 3. Следующими были занумерованы виды третьего шага эволюции – подвиды вида 2 получили номера 4 и 5, а вида 3 – номера 6 и 7, и т.д.

Напишите программу, которая по номерам двух видов вычислит номер вида их ближайшего общего предка в дереве эволюции.

Входные данные

Первая строка входного файла содержит целое число N (1≤N≤100) – количество этапов эволюции, которые произошли на планете Олимпия до текущего времени. Вторая и третья строки файла содержат по одному натуральному числу, которые представляют номера видов, для которых требуется найти номер их ближайшего общего предка.

Выходные данные

Единственная строка выходного файла должна содержать натуральное число – номер ближайшего предка для двух видов.

Примеры
Входные данные
4
15
12
Выходные данные
3
Входные данные
18
233016
233008
Выходные данные
14563
Страница: << 13 14 15 16 17 18 19 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест