Линейные структуры(59 задач)
Корневая эвристика (sqrt декомпозиция)(14 задач)
Разреженные таблицы (sparse table)(2 задач)
Система непересекающихся множеств(16 задач)
Хеш(35 задач)
Персистентные структуры данных(2 задач)
Юная программистка Агнесса недавно узнала на уроке информатики об арифметических выражениях. Она заинтересовалась вопросом, что случится, если из арифметического выражения удалить всё, кроме скобок. Введя запрос в своём любимом поисковике, она выяснила, что математики называют последовательности скобок, которые могли бы встречаться в некотором арифметическом выражении, правильными скобочными последовательностями.
Так, последовательность ()(()) является правильной скобочной последовательностью, потому что она может, например, встречаться в выражении (2+2) : (3–(5–2)+4), а последовательности (() и ())( не являются таковыми. Легко видеть, что существует пять правильных скобочных последовательностей, состоящих ровно из шести скобок (по три скобки каждого типа — открывающих и закрывающих): ((())), (()()), (())(), ()(()) и ()()().
Агнесса заинтересовалась простейшими преобразованиями правильных скобочных последовательностей. Для начала Агнесса решила ограничиться добавлением скобок в последовательность. Она очень быстро выяснила, что после добавления одной скобки последовательность перестаёт быть правильной, а вот добавление двух скобок иногда сохраняет свойство правильности. Например, при добавлении двух скобок в различные места последовательности ()() можно получить последовательности (()()), (())(), ()(()) и ()()(). Легко видеть, что при любом способе добавления двух скобок с сохранением свойства правильности одна из новых скобок должна быть открывающей, а другая — закрывающей.
Агнесса хочет подсчитать количество различных способов добавления двух скобок в заданную правильную скобочную последовательность так, чтобы снова получилась правильная скобочная последовательность. К сожалению, выяснилось, что это количество может быть в некоторых случаях очень большим. Агнесса различает способы получения последовательности по позициям добавленных скобок в полученной последовательности. Например, даже при добавлении скобок в простейшую последовательность () можно получить другую правильную скобочную последовательность семью способами: ()(), (()), (()), (()), (()), ()(), ()(). Здесь добавленные скобки выделены жирным шрифтом.
Таким образом, если в полученной последовательности добавленная открывающая скобка стоит в позиции \(i\), а добавленная закрывающая — в позиции \(j\), то два способа, соответствующие парам \((i_1, j_1)\) и \((i_2, j_2)\), считаются различными, если \(i_1\neq i_2\) или \(j_1\neq j_2\).
Требуется написать программу, которая по заданной правильной скобочной последовательности определяет количество различных описанных выше способов добавления двух скобок.
Входной файл состоит из одной непустой строки, содержащей ровно \(2n\) символов: \(n\) открывающих и \(n\) закрывающих круглых скобок. Гарантируется, что эта строка является правильной скобочной последовательностью.
Выведите в выходной файл количество различных способов добавления в заданную последовательность двух скобок таким образом, чтобы получилась другая правильная скобочная последовательность.
Данная задача содержит три подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
Величина \(n\) (количество скобок каждого типа) не превосходит 50.
Величина \(n\) (количество скобок каждого типа) не превосходит 2500.
Величина \(n\) (количество скобок каждого типа) не превосходит 50 000.
()
7
()()
17
(())
21
К 50-летию первого пилотируемого полета в космос решено создать новый тип космического корабля многоразового использования “Восторг”. Прямоугольная часть его корпуса (далее прямоугольник) должна быть облицована квадратными термозащитными плитками разных цветов одного и того же размера. Прямоугольник состоит из \(r\) рядов по \(c\) плиток в каждом. Плитки должны образовывать заданный рисунок.
Облицовка космического корабля отдельными плитками очень трудоемка, поэтому для выкладывания заданного рисунка используются одинаковые прямоугольные панели, состоящие из плиток. Панели крепятся на корпусе одна за другой, заполняя ряд за рядом сверху вниз. Каждый ряд панелей может быть сдвинут относительно предыдущего на одно и то же число плиток. При этом панели могут выходить за пределы прямоугольника. Панели должны быть одинаково ориентированы, то есть при параллельном переносе одной панели на место другой цвета образующих эти панели плиток должны совпадать.
Главный конструктор хочет выбрать такой размер панели \(a\times b\) и сдвиг \(s\), чтобы этими панелями можно было выложить заданный рисунок, и площадь панели была минимальна.
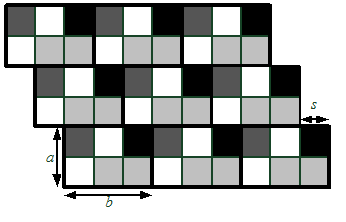
Требуется написать программу, которая по заданному расположению плиток в прямоугольнике рассчитывает размеры минимальной по площади панели, которую можно использовать при его облицовке, а также величину сдвига вправо (\(0 \leq s < b\)) каждого следующего ряда относительно предыдущего.
Первая строка входного файла содержит два целых числа: \(r\) и \(c\) – размеры прямоугольника в плитках. В последующих \(r\) строках указаны цвета плиток фрагмента. Каждый из \(k \leq 26\) цветов обозначен одной из первых \(k\) прописных букв латинского алфавита. Гарантируется, что для этого прямоугольника можно подобрать панель размера \(a\times b\), такую, что \(2a \leq r\) и \(2b \leq c\).
ВВ выходной файл необходимо вывести три целых числа \(a\), \(b\) и \(s\), удовлетворяющих условиям задачи. Если решений несколько, разрешается вывести любое из них.
Во втором примере облицовка прямоугольника соответствуют следующему рисунку (выступающие за границы прямоугольника части панелей не показаны):

Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 20.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 200.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 1961.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 20.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 200.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 500.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 1961.
2 4 ABAB ABAB
1 2 0
5 7 DCADCAD BABBABB ADCADCA BBABBAB CADCADC
2 3 1
Игорь работает младшим лаборантом в НИИ ихтиологии. Ему вверены \(n\) аквариумов, стоящих в ряд, в каждом из которых живет колония рыбок гуппи. Про каждую колонию заранее известна ее численность.
В лабораторных условиях НИИ ихтиологии колония рыбок гуппи растет по следующему правилу: достигнув популяции в \(f\) рыбок, колония живет в течении \(max(1000 - f, 1)\) секунд, после чего на свет появляется новая рыбка. От начального момента времени до рождения первой рыбки колония размера \(f\) также ждет \(max(1000 - f, 1)\) секунд.
Например, колония с начальным размером 996 будет размножаться следующим образом:
| момент времени | размер колонии | время до очередной рыбки |
|---|---|---|
| 0 | 996 | 4 |
| 4 | 997 | 3 |
| 7 | 998 | 2 |
| 9 | 999 | 1 |
| 10 | 1000 | 1 |
| 11 | 1001 | 1 |
| 12 | 1002 | 1 |
| ... | ... | ... |
Появление на свет каждой новой рыбки Игорь должен фиксировать в специальном журнале. Будем считать, что запись он делает мгновенно, но при этом он должен в момент рождения новой рыбки находиться рядом с аквариумом, в котором это произошло.
На перемещение от одного аквариума к соседнему у Игоря уходит одна секунда. В начальный момент времени Игорь стоит около первого аквариума.
Вычислите, в течение какого наибольшего периода времени Игорь сможет добросовестно выполнять свою работу.
В первой строке входного файла содержится целое число \(n\) (\(2 \le n \le 50\)) - количество аквариумов с рыбками гуппи в НИИ ихтиологии. Каждая из следующих \(n\) строк содержит одно целое число \(a_i\) (\(1 \le a_i \le 2007\)) - численность \(i\)-й колонии.
В выходной файл выведите момент времени, когда родится первая рыбка гуппи, запись о рождении которой Игорь сделать не сможет.
В приведенном примере Игорь сначала ждет у первого аквариума появления рыбки на 4-й секунде. После этого он бежит к третьему аквариуму (на это у него уходит 2 секунды) и как раз успевает к рождению рыбки на 6-й секунде. Однако вернуться к первому аквариуму, где следующая рыбка родится на 7-й секунде, он уже не успевает.
3 996 1 994
7
Дана строка, составленная из круглых скобок. Определите, какое наименьшее количество символов необходимо удалить из этой строки, чтобы оставшиеся символы образовывали правильную скобочную последовательность.
Во входном файле записана строка из круглых скобок. Длина строки не превосходит \({100\,000}\) символов.
Выведите единственное целое число — ответ на поставленную задачу.
())(()
2
))(((
5
Напишите программу, которая будет обрабатывать последовательность запросов таких видов:
CLEAR — сделать пирамиду пустой (если в пирамиде уже были какие-то элементы, удалить все). Действие происходит только с данными в памяти, на экран ничего не выводится.
ADD n — добавить в пирамиду число n. Действие происходит только с данными в памяти, на экран ничего не выводится.
EXTRACT — вынуть из пирамиды максимальное значение. Следует и изменить данные в памяти, и вывести на экран или найденное максимальное значение, или, если пирамида была пустой, слово "CANNOT" (большими буквами).
Во входных данных записано произвольную последовательность запросов CLEAR, ADD и EXTRACT — каждый в отдельной строке, согласно вышеописанному формату.
Суммарное количество всех запросов не превышает 200000.
Для каждого запроса типа EXTRACT выведите на стандартный выход (экран) его результат (в отдельной строке).
Задачу следует решить двумя способами. Один — использовать стандартную реализацию пирамиды в STL; она называется priority_queue, для её использования необходимо подключить заголовочный файл queue. Другой способ — реализовать пирамиду самому, использовать разрешено лишь некоторые из следующих заголовочных файлов: iostream, fstream, сstdio, stdio.h, string, string.h, vector.
ADD 192168812 ADD 125 ADD 321 EXTRACT EXTRACT CLEAR ADD 7 ADD 555 EXTRACT EXTRACT EXTRACT
192168812 321 555 7 CANNOT