Темы --> Информатика --> Структуры данных
    Деревья(174 задач)
    Линейные структуры(59 задач)
    Корневая эвристика (sqrt декомпозиция)(14 задач)
    Разреженные таблицы (sparse table)(2 задач)
    Система непересекающихся множеств(16 задач)
    Хеш(35 задач)
    Персистентные структуры данных(2 задач)
---> 279 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 33 34 35 36 37 38 39 >> Отображать по:
#111240
Переворот
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Дан массив. Надо научиться обрабатывать два типа запросов.

* 1 L R - перевернуть отрезок \([L,\,R]\)

* 2 L R - найти минимум на отрезке \([L,\,R]\)

Входные данные

Первая строка файла содержит два числа \(n\), \(m\). (\(1 \le n,m \le 10^5\)) Во второй строке находится \(n\) чисел \(a_i\) (\(1 \le a_i \le 10^9\)) — исходный массив. Остальные \(m\) строк содержат запросы, в формате описанном в условии. Для чисел \(L\), \(R\) выполняется ограничение (\(1 \le L \le R \le n\)).

Выходные данные

На каждый запрос типа 2, во входной файл выведите ответ на него, в отдельной строке.

Примеры
Входные данные
10 7
5 3 2 3 12 6 7 5 10 12
2 4 9
1 4 6
2 1 8
1 1 8
1 8 9
2 1 7
2 3 6
Выходные данные
3
2
2
2
#111253
Гистограмма
  
Темы: [Стек]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Гистограмма является многоугольником, сформированным из последовательности прямоугольников, выровненных на общей базовой линии. Прямоугольники имеют равную ширину, но могут иметь различные высоты. Например, фигура слева показывает гистограмму, которая состоит из прямоугольников с высотами 2, 1, 4, 5, 1, 3, 3. Все прямоугольники на этом рисунке имеют ширину, равную 1.

Обычно гистограммы используются для представления дискретных распределений, например, частоты символов в текстах. Отметьте, что порядок прямоугольников очень важен. Вычислите область самого большого прямоугольника в гистограмме, который также находится на общей базовой линии. На рисунке справа заштрихованная фигура является самым большим выровненным прямоугольником на изображенной гистограмме.

Входные данные

В первой строке входного файла записано число \(N\) (\(0\) < \(N\) ≤ \(10^6\)) - количество прямоугольников гистограммы. Затем следует \(N\) целых чисел \(h_1 ... h_n\), где \(0\) ≤ \(h_i\) ≤ \(10^9\). Эти числа обозначают высоты прямоугольников гистограммы слева направо. Ширина каждого прямоугольника равна \(1\)

Выходные данные

Выведите площадь самого большого прямоугольника в гистограмме. Помните, что этот прямоугольник должен быть на общей базовой линии.

Примеры
Входные данные
7 2 1 4 5 1 3 3
Выходные данные
8
#111491
Березовая аллея
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

На краю деревни растет старая березовая аллея. Аллея имеет форму прямой полосы шириной \(W\) метров. Вдоль левой стороны аллеи растет \(N\) берез, а вдоль правой — \(M\) берез, при этом \(i\)-я береза с левой стороны аллеи находится на расстоянии \(a_i\) метров от начала аллеи, а \(j\)-я береза с правой стороны — на расстоянии \(b_j\) метров от начала аллеи.

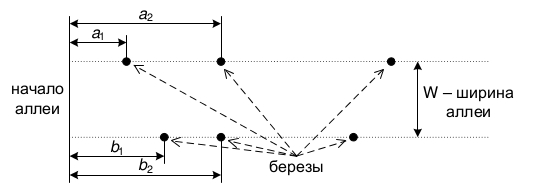
Отдыхая в деревне прошедшим летом, один юный информатик обнаружил, что кору берез стали грызть зайцы. Чтобы защитить деревья от зайцев, мальчик решил окружить березы красной лентой (зайцы не любят красный цвет и не станут заходить на огражденную лентой территорию. К сожалению, в его распоряжении оказалась только лента длиной \(L\) метров, которую, к тому же, нельзя было разрезать. Единственное, что можно было делать в этом случае — окружить этой лентой как можно больше берез. При этом, чтобы сохранить аллею, необходимо окружить на каждой стороне аллеи хотя бы одну березу.

Требуется написать программу, которая по заданной длине ленты, ширине аллеи и положению берез на ней определяет максимальное число берез, которое можно окружить этой лентой. Считается, что березы представляются точками, толщиной берез и шириной ленты следует пренебречь.

Входные данные

Первая строка входного файла содержит два разделенных пробелом целых числа: длину ленты \(L\) и ширину аллеи \(W\) (\(1 \leq L \leq 2 \times 10^5\), \(1 \leq W \leq 10^4\)).

Вторая и третья строки описывают березы вдоль левой стороны аллеи. Вторая строка содержит число \(N\) — количество берез (\(1 \leq N \leq 2000\)), а третья строка содержит \(N\) различных целых чисел \(a_1\), \(a_2\), …, \(a_N\) (\(0 \leq a_i \leq 10^5\)), заданных по возрастанию.

Четвертая и пятая строки описывают березы вдоль правой стороны аллеи. Четвертая строка содержит число \(M\) — количество берез (\(1 \leq M \leq 2000\)), а пятая строка содержит \(M\) различных целых чисел \(b_1\), \(b_2\), …, \(b_M\) (\(0 \leq b_i ≤ 10^5\)), заданных по возрастанию.

Выходные данные

Выходной файл должен содержать одно целое число: максимальное количество берез, которое можно оградить заданной лентой.

Гарантируется, что если максимальное число берез, которое можно оградить лентой длины L, равно X, то нет способа оградить (X + 1) березу лентой длины (L + \(10^{-5}\)).

Система оценивания

Правильные решения для тестов, в которых 1 ≤ N + M ≤ 50, будут оцениваться из 30 баллов.

Правильные решения для тестов, в которых 1 ≤ N + M ≤ 500, будут оцениваться из 60 баллов.

Примеры
Входные данные
18 4
3
0 3 6
4
0 3 6 10
Выходные данные
5
Входные данные
5 3
1
0
1
0
Выходные данные
0
#111572
Военный полигон
  
Ограничение по времени, сек0.75
Ограничение по памяти, мегабайт256





Министерство обороны Флатландии планирует построить новый военный полигон. Полигон должен иметь форму круга.

Поскольку генералы в министерстве волнуются о секретности проводимых на полигоне испытаний, он должен быть надежно защищен. Флатландия защищена сверху несколькими специальными силовыми щитами, каждый из них имеет форму прямоугольника со сторонами, параллельными осям координат. Генералы хотят выбрать такое место для полигона, где он был бы полностью защищен хотя бы двумя конкретными силовыми щитами (недостаточно, чтобы каждая точка просто была защищена хотя бы двумя щитами, должно быть два щита, каждый из которых защищает полигон полностью).

Конечно, генералы хотят построить полигон максимального возможного размера. Помогите им выбрать такое место для полигона, чтобы он имел максимальный возможный радиус.

Входные данные

Первая строка входного файла содержит число \(N\) — количество силовых щитов. Каждая из следующих N строк описывает силовой щит (\(1 \leq N \leq 200000\)). Описание представляет собой четверку координат: \(x_{min}\), \(y_{min}\), \(x_{max}\), \(y_{max}\). Все координаты целые и не превышают 100000 по абсолютной величине.

Выходные данные

Выведите три вещественных числа — координаты центра полигона и его радиус. Все числа следует выводить ровно с одним знаком после десятичной точки.

Если построить полигон невозможно, выведите “Impossible” на первой строке выходного файла.

Примеры тестов
Входные данные
4
0 0 2 3
1 -1 4 1
1 1 4 4
2 0 5 5
Выходные данные
3.0 2.0 1.0
Входные данные
1
0 0 1 1
Выходные данные
Impossible
Входные данные
2 
0 0 3 3
0 0 3 3
Выходные данные
1.5 1.5 1.5
Решения, работающие при \(1 \leq N \leq 5 000\), будут набирать не менее 50 баллов
#111582
Гарри Поттер и Зал Пророчеств
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Отряд Дамблдора готовится к полёту в Отдел Тайн Министерства Магии. Так как на их пути за Пророчеством могут встретиться слуги Волан-де-Морта, Гарри с Невиллом решили потренироваться в дуэльных боях.

Они решили провести \(n\) раундов дуэли, а после каждого раунда выпивать восстанавливающее зелье, чтобы не тратить лишних сил. Всего у ребят \(2n\) зелий. После каждого раунда дуэли они выбирают два наиболее близких по мощности восстанавливающих зелья. Из нескольких таких пар они выбирают ту, у которой сумма мощностей наибольшая. Затем Невилл выпивает более мощное зелье из пары, а Гарри - менее мощное.

Помогите Гарри с Невиллом определить, какие зелья и в каком порядке выпьет каждый из них.

Формат входного файла

Первая строка входного файла содержит одно целое число \(n\) (\(1 \le n \le 100\,000\)) - количество раундов дуэли. Во второй строке входного файла содержится \(2n\) целых чисел \(a_1, a_2, \ldots, a_{2n}\) (\(1\le a_i \le 10^9\)), где \(a_i\) - мощность \(i\)-го восстанавливающего зелья.

Формат выходного файла

В первой строке выведите \(n\) чисел - мощности зелий, которые выпьет Невилл. Во второй строке выведите \(n\) чисел - мощности зелий, которые выпьет Гарри. Зелья надо выводить в том порядке, в котором Невилл и Гарри должны их выпивать.

Примеры
Входные данные
1
3 6
Выходные данные
6
3
Входные данные
2
11 43 56 22
Выходные данные
22 56
11 43
Страница: << 33 34 35 36 37 38 39 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест