Темы --> Информатика --> Структуры данных
    Деревья(174 задач)
    Линейные структуры(59 задач)
    Корневая эвристика (sqrt декомпозиция)(14 задач)
    Разреженные таблицы (sparse table)(2 задач)
    Система непересекающихся множеств(16 задач)
    Хеш(35 задач)
    Персистентные структуры данных(2 задач)
---> 279 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 49 50 51 52 53 54 55 >> Отображать по:
#113784
Количество соседних цветов
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
512 megabytes

Дан неориентированный граф без петель и кратных ребер, у которого n вершин и m ребер. У каждой вершины есть цвет. Требуется ответить на q запросов. Каждый запрос имеет один из двух типов:

1 v c – перекрасить вершину v в цвет c

2 v – вычислить количество различных цветов у соседей вершины v .

Входные данные

В первой строке даны три целых числа n , m и q ( 1 ≤ n ≤ 10 5 , 1 ≤ m , q ≤ 2·10 5 ).

Во второй строке через пробел даны n целых чисел 1 ≤ c 1 , ..., c n ≤ n – цвета вершин.

В следующих m строках заданы по два целых числа u и v – номера вершин, которые соединяет очередное ребро ( 1 ≤ u , v ≤ n , u ≠ v ).

В следующих q строках заданы запросы. Каждый запрос имеет один из двух типов:

1 v c – перекрасить вершину v в цвет c , 1 ≤ v , c ≤ n .

2 v – вычислить количество различных цветов у соседей вершины v , 1 ≤ v ≤ n .

Выходные данные

Для каждого запроса второго типа выведите в отдельной строке ответ на него.

Примеры
Входные данные
4 3 3
1 2 3 4
1 2
1 3
1 4
2 1
1 4 3
2 1
Выходные данные
3
2
#113785
Количество элементов < x и инкремент на отрезке
  
ограничение по времени на тест
8.0 second;
ограничение по памяти на тест
256 megabytes

Для заданного массива требуется выполнить ряд запросов. Все запросы делятся на два типа. Запрос первого типа – вычислить количество элементов массива на отрезке от l до r меньших заданного числа x . Запрос второго типа – увеличить все элементы массива на отрезке от l до r на заданное число x .

Входные данные

В первой строке заданы два целых числа n и q – размер массива и количество запросов ( 1 ≤ n , q ≤ 2·10 5 ).

Во второй строке через пробел заданы n целых чисел - 10 9 ≤ a 1 , ..., a n ≤ 10 9 – элементы массива.

В следующих q строках содержатся запросы. Каждый из запросов имеет один из двух видов:

1 l r x – запрос количества элементов на отрезке от l до r меньших заданного числа x ( 1 ≤ l ≤ r ≤ n , - 10 9 ≤ x ≤ 10 9 ).

2 l r x – запрос инкремента на величину x на отрезке от l до r ( 1 ≤ l ≤ r ≤ n , - 10 6 ≤ x ≤ 10 6 ).

Выходные данные

На каждый запрос первого типа выведите в отдельной строке ответ на этот запрос.

Примеры
Входные данные
5 3
1 2 3 4 5
1 1 5 5
2 2 4 2
1 1 5 5
Выходные данные
4
2
#113809
Простыни
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

В один прекрасный день маленький Дональд решил вымыть N своих чистых белых простыней. После мытья он положил их на землю во дворе, чтобы их высушить. Дональд помещал простыни так, чтобы никакие две простыни не касались ни сторонами, ни углами, и чтобы их стороны не пересекалась, но возможно, что он разместил меньшие простыни поверх более крупных или что простыня полностью закрывает какие-то другие простыни. Сделав это, Дональд лег спать.

Друг Дональда Ким как-то узнал о том, что Дональд сушит простыни и решил пообщаться с ним. Он нашел пейнтбольный пистолет своего отца на чердаке. Наряду с пистолетом у него было несколько пейнтбольных мячей, каждый из них имел свой цвет (не обязательно уникальный). Как только Дональд заснул, Ким вошёл во двор к Дональду и начал стрелять пр простыням из пейнтбольного пистолета. Простыни Дональда очень тонкие, поэтому, когда Ким попадает в какую-то простыню, она пропускает краску дальше, на простыню ниже (и та тоже, и так происходит, пока не закончатся простыни и краска не попадет на землю). После того, как Ким использовал все шары, он с радостью покинул двор Дональда. Дональд был очень расстроен, увидев, что случилось с его простынями. Дональд очень заинтересован в правильных данных о преступлении Кима, но он в шоке и не способен думать, поэтому просит вас сказать ему количество цветов на каждой простыне.

Мы можем представлять двор Дональда как бесконечную систему координат, а простыни - как прямоугольники, параллельные осям координат. Выстрелы Кима могут быть представлены как точки в этой системе.

Когда-то в детстве дедушка рассказал Киму, что снаряд никогда не попадает в одну воронку дважды, так что координаты всех выстрелов попарно различны.

Входные данные

Первая строка ввода содержит два числа - количество простынь N ( 1 ≤ N ≤ 80000 ), и количество шаров M ( 1 ≤ M ≤ 80 000 ).

i -я из следующих N строк содержит четыре числа: координаты нижнего левого угла A i , B i ( 1 ≤ A i , B i ≤ 10 9 ) и верхнего правого угла C i , D i , ( 1 ≤ C i , D i ≤ 10 9 ) i -й простыни.

j -я из следующих M строк содержит три числа, где X j , Y j ( 1 ≤ X j , Y j ≤ 10 9 ) - координаты j -го выстрела Кима и K j ( 1 ≤ K j ≤ 10 9 ) - цвет j -го пейнтбольного шара.

Выходные данные

i -я из N выходных строк должна содержать количество цветов на i -м листе.

Система оценки

Тесты к данной задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп.

Примеры
Входные данные
2 2
1 1 3 3
5 6 10 10
3 3 1
5 1 2
Выходные данные
1
0
Входные данные
3 3
1 1 7 7
2 2 6 6
3 3 5 5
4 4 1
2 6 2
4 7 3
Выходные данные
3
2
1
Входные данные
1 3
1 1 7 7
2 6 2
4 7 3
4 4 1
Выходные данные
3
#113813
Небоскрёбы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

Вы когда-нибудь мечтали стать главным героем компьютерной игры? Главный герой этой истории, Бранимир, мечтает сейчас именно об этом.

Мир в мечте Бранимира состоит из N небоскребов, пронумерованных слева направо. Для i -го небоскреба, известна его высота H i и количество золотых монет G i на крыше этого небоскреба. Игра начинается с прыжка на любой из небоскребов и состоит из нескольких ходов. На каждом ходу Бранимир может прыгнуть на любой небоскрёб, находящийся справа от него, но так, чтобы высота нового небоскрёба была не меньше того небоскрёба, на котором сейчас сидит Бранимир. Оказавшись на крыше небоскреба, Бранимир собирает все золотые монеты на ней. Бранимир может закончить игру после любого количества шагов (возможно, нулевого), но он должен собрать не менее K золотых монет, чтобы перейти на следующий уровень.

Бранимир хочет узнать, сколько существует способов сыграть в эту игру так, чтобы перейти на следующий уровень. Две игры называются разными, если существует небоскреб который был посещен в одной игре, но не был посещён в другой.

Входные данные

Первая строка содержит 2 натуральных числа N и K ( 1 ≤ N ≤ 40 , 1 ≤ K ≤ 4·10 10 ) — число небоскрёбов и количество монет, которые надо набрать соответственно.

Следующие N строк содержат информацию о небоскрёбах. В i -й строке даны 2 числа H i и G i ( 1 ≤ H i , G i ,  ≤ 10 9 ) — высота и количество монет на i -м небоскрёбе.

Выходные данные

В единственной строке вывода выведите число возможных игр, в которых Бранимир сможет пройти на следующий уровень.

Система оценки

Решение, корректно работающее при n ≤ 20 будет оцениваться в 40 баллов.

Примеры
Входные данные
4 6
2 1
6 3
7 2
5 6
Выходные данные
3
Входные данные
2 7
4 6
3 5
Выходные данные
0
Входные данные
4 15
5 5
5 12
6 10
2 1
Выходные данные
4
#113894
Сжатие таблицы
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
256 megabytes

Петя увлёкся алгоритмами сжатия данных. Он уже изучил форматы gz , bz , zip и несколько других. Воодушевившись новыми знаниями, Петя собрался разработать свой формат сжатия и назвать его dis .

Петя решил сжимать таблицы. У него есть таблица, состоящая из n строк и m столбцов, заполненная целыми положительными числами. Он хочет заменить значения элементов таблицы на целые положительные числа так, чтобы отношение элементов в каждой строке и каждом столбце не изменилось. То есть, если в некоторой строке исходной таблицы a i , j < a i , k , то и в сжатой таблице a ' i , j < a ' i , k , и если a i , j = a i , k , то a ' i , j = a ' i , k . Аналогично, если в некотором столбце исходной таблицы a i , j < a p , j , то и в сжатой таблице a ' i , j < a ' p , j , и если a i , j = a p , j , то a ' i , j = a ' p , j .

Поскольку б'{о}льшие значения требуют больше места для хранения, максимальное значение элемента получившейся матрицы должно быть как можно меньше.

В теории Петя мастер, но вот писать код он не любит. Помогите ему реализовать формат сжатия dis .

Входные данные

В первой строке входных данных содержатся два числа n и m ( 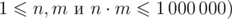— количество строк и столбцов таблицы соответственно.

В следующих n строках содержится по m целых чисел a i , j (1 ≤ a i , j ≤ 10 9 ) — значения элементов таблицы.

Выходные данные

Выведите сжатую таблицу: n строк, содержащих по m чисел.

Если существует несколько ответов, минимизирующих максимальное число, то разрешается вывести любой из них.

Система оценки

Тесты к этой задаче состоят из восьми групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

Примечание

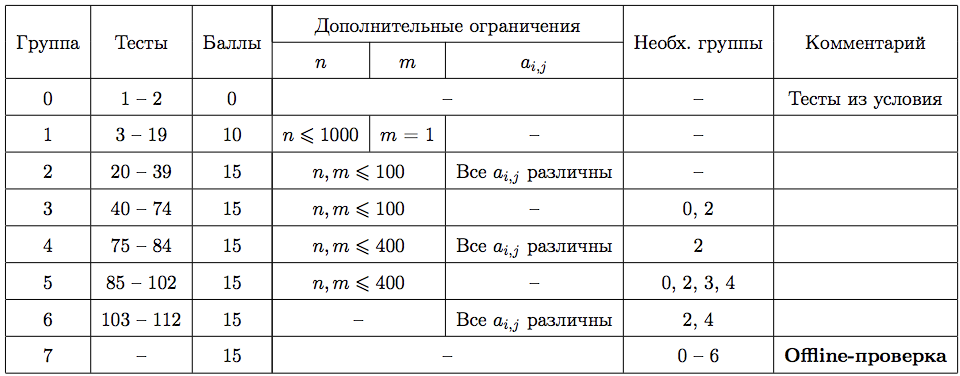
В первом примере a 1, 2 ≠ a 2, 1 , но, поскольку они не располагаются в одной строке или в одном столбце, при сжатии их можно сделать равными.

Примеры
Входные данные
2 2
1 2
3 4
Выходные данные
1 2
2 3
Входные данные
4 3
20 10 30
50 40 30
50 60 70
90 80 70
Выходные данные
2 1 3
5 4 3
5 6 7
9 8 7
Страница: << 49 50 51 52 53 54 55 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест