--->
78 задач
<---
Источники
#586
Для N человек известно 3 параметра: время надувания шарика, сколько шариков можно надуть до отдыха и время отдыха. Требуется определить, за какое минимальное время эти люди надуют N шариков.
Организаторы детского праздника планируют надуть для него \(M\) воздушных шариков. С этой целью они пригласили \(N\) добровольных помощников, \(i\)-й среди которых надувает шарик за \(T_i\) минут, однако каждый раз после надувания \(Z_i\) шариков устает и отдыхает \(Y_i\) минут. Теперь организаторы праздника хотят узнать, через какое время будут надуты все шарики при наиболее оптимальной работе помощников, и сколько шариков надует каждый из них. (Если помощник надул шарик, и должен отдохнуть, но больше шариков ему надувать не придется, то считается, что он закончил работу сразу после окончания надувания последнего шарика, а не после отдыха).
Входные данные
В первой строке входных данных задаются числа \(M\) и \(N\) (0 <= \(M\) <= 15000, 1 <= \(N\) <= 1000). Следующие \(N\) строк содержат по три целых числа - \(T_i\), \(Z_i\) и \(Y_i\) соответственно (1 <= \(T_i\), \(Y_i\) <= 100, 1 <= \(Z_i\) <= 1000).
Выходные данные
Выведите в первой строке число \(T\) - время, за которое будут надуты все шарики. Во второй строке выведите \(N\) чисел - количество шариков, надутых каждым из приглашенных помощников. Разделяйте числа пробелами. Если распределений шариков несколько, выведите любое из них.
Примеры
Входные данные
2 2 1 1 1 1 1 1
Выходные данные
1 1 1
Входные данные
3 2 2 2 5 1 1 10
Выходные данные
4 2 1
#598
Темы:
[Задачи на моделирование]
[Очередь]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Окружная олимпиада,
2007,
1 тур,
Задача A
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Петя недавно узнал о существовании игры маджонг. Она ему показалась настолько интересной, что он играет в нее целыми днями. Для этой игры необходима прямоугольная доска размером m n полей и набор фишек разных цветов. При этом фишек каждого цвета в наборе должно быть ровно две. В начале игры фишки располагаются на доске произвольным образом.
После этого за один ход разрешается снять пару фишек одного цвета, если они обе являются самыми правыми в своих горизонталях, либо самыми левыми в своих горизонталях, либо самыми нижними в своих вертикалях, либо самыми верхними в своих вертикалях. Если соответствующей пары фишек нет, то игра закончена.
Цель игры состоит в том, чтобы сделать как можно больше ходов.
Задана начальная расстановка фишек на доске. Требуется найти самую длинную последовательность ходов, которую может сделать Петя из заданной позиции.
Входные данные
Первая строка входного файла содержит размеры доски: два целых числа \(m\) и \(n\) (1 ≤ \(m\), \(n\) ≤ 300, хотя бы одно из этих чисел четно). Далее следуют \(m\) строк по \(n\) чисел в каждой, \(j\)-е число в \(i\)-й из этих строк представляет собой номер цвета \(j\)-й слева фишки в \(i\)-й горизонтали. Цвета пронумерованы натуральными числами от 1 до \(n\)*\(m\) / 2. На доске ровно две фишки каждого цвета.
Выходные данные
В первой строке выходного файла выведите \(k\) — максимальное количество ходов, которое может сделать Петя из заданной начальной позиции. Во второй строке выходного файла выведите разделенные пробелами \(k\) чисел — номера цветов фишек в том порядке, в котором они должны сниматься с доски. Если возможных ответов несколько, выведите любой.
Примеры
Входные данные
1 2 1 1
Выходные данные
1 1
Входные данные
4 1 1 2 2 1
Выходные данные
2 2 1
#855
Темы:
[Стек]
[Задачи на моделирование]
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2008,
Лига А,
Задача B
]
Необходимо упорядочить числа с помощью стека.
К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.
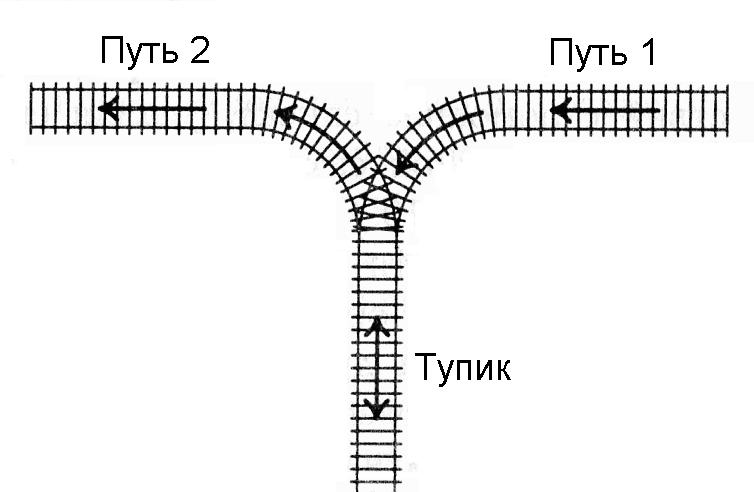
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).
Входные данные
Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.
Выходные данные
Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:
- если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
- если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).
Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.
Если выстроить вагоны по порядку невозможно, выведите одно число 0.
Примеры
| Входные данные | Выходные данные |
| 3 3 2 1 | 1 3 2 3 |
| 4 4 1 3 2 | 1 2 2 1 1 2 2 3 |
| 3 2 3 1 | 0 |
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Имя входного файла: fitness.in
Имя выходного файла: fitness.out
В последнее время фитнесс-клубы стали очень популярны среди жителей столицы Флатландии. В такие клубы люди ходят после работы для того, чтобы поддерживать себя в хорошей физической форме. В фитнесс-клубe «Флат» каждому из посетителей на время посещения выделяется один из \(k\) шкафчиков, в который он может убрать свои вещи на время тренировки.
В течение дня в фитнесс-клубе проходит \(n\) тренировок, причем каждый из посетителей приходит к началу какой-либо из этих тренировок (в этот момент он получает ключ от шкафчика) и уходит сразу после ее окончания (в этот момент он сдает ключ от шкафчика). При этом можно считать, что все посетители, закончившие тренировку, уходят раньше, чем все посетители, пришедшие на следующую тренировку.
Некоторые из посетителей уходя закрывают шкафчик, а другие не закрывают. Так как все посетители фитнесс-клуба посещают его уже достаточно давно, то про каждого из них персонал клуба знает, закроет ли он свой шкафчик, когда будет уходить. Таким образом, для каждой трени- ровки известно два числа: число \(a_i\) посетителей, которые закроют шкафчик, и число \(b_i\) посетителей, которые не закроют.
В начале дня все \(k\) шкафчиков закрыты. Разумеется, персоналу клуба хочется, чтобы в конце дня также как можно больше шкафчиков были закрыты тогда надо будет меньше работать при подготовке к очередному дню. Для того, чтобы достичь этой цели, персонал может выдавать ключи от шкафчиков посетителям произвольным образом. Например, имеет смысл выдавать ключ от открытого шкафчика тому, кто его точно закроет.
Необходимо найти максимальное число шкафчиков, которые окажутся закрытыми, в случае оптимальных действий персонала фитнесс-клуба.
Входные данные
Первая строка входного файла содержит два целых числа: \(n\) (\(1 \leq n \leq 100\)) и \(k\) (\(1 \leq k \leq 1000\)) Каждая из последующих \(n\) строк содержит по два целых числа \(a_i\) и \(b_i\) (\(0 \leq a_i, b_i \leq k\), \(a_i + b_i \leq k\)).
Выходные данные
В выходной файл выведите одно число — ответ на задачу.
Примечание
Пронумеруем шкафчики числами от 1 до 4. Посетителям, пришедшим на первую тренировку
выдадим ключи так: тому, кто закроет, от шкафчика 1, тем, кто не закроет, от 2 и 3. Посетителям, пришедшим на вторую тренировку, выдадим ключи так: тому, кто закроет, номер 2,
тому, кто не закроет, номер 3. В итоге открытым после окончания дня останется только шкафчик
номер 3.
Примеры
Входные данные
2 4 1 2 1 1
Выходные данные
3
Черепаха стоит на краю грядки. На грядки растут одуванчики, для каждого из них задано время и место всхода. Одуванчики прорастают последовательно, также задана скорость черепахи и время съедания одуванчика. Необходимо определить минимальное время, за которое можно съесть все одуванчики и вернуться.
Домик черепахи расположен в начале прямой узкой грядки, на которой должны прорасти одуванчики – ее любимое лакомство. И вот черепахе приснился вещий сон. Из него она узнала, что наконец-то после полуночи начнут расти одуванчики. Ей даже приснилось, в какой момент времени, и в какой точке грядки вырастет каждый одуванчик. Ровно в полночь черепаха выползла из домика, чтобы съесть все одуванчики и до следующей полуночи вернуться домой.
Черепаха может ползти со скоростью, не превосходящей величины vmax. Одуванчик она съедает, остановившись на время d. Если одуванчик начать есть, но не доесть до конца, то он засыхает, поэтому его надо съедать за один прием. Одуванчики прорастают тем позже, чем дальше они расположены от начала грядки. В одной точке не могут прорастать несколько одуванчиков, а также несколько одуванчиков не могут прорастать в один момент времени.
Требуется определить, в какой момент времени черепаха сможет вернуться домой, съев все одуванчики и затратив на путешествие наименьшее время.
Входные данные
В 1-й строке входного файла находятся 2 целых числа, разделенные пробелом: vmax (в см/мин) и d (в минутах), 0 < vmax ≤ 200, 0 ≤ d ≤ 500.
Во 2-й строке находится число N – количество одуванчиков (в штуках). 0 ≤ N ≤ 1400 при d = 0, в противном случае 0 ≤ N ≤ 200.
В каждой из последующих N строк расположены: целое число xi – расстояние от одуванчика до начала грядки (в сантиметрах), 0 ≤ xi ≤ 32767, и через пробел ti – момент прорастания одуванчика (в формате hh:mm). Пары приведены в порядке возрастания расстояний.
Выходные данные
Выходной файл должен содержать момент времени возвращения черепахи домой (в формате hh:mm), округленный до целых минут в большую сторону.
Примечания
1. В часе – 60 минут, в сутках – 24 часа.
2. Время в сутках изменяется от 00:00 до 23:59.
3. Можете считать, что черепаха не меняет направления движения до тех пор, пока не доползет до последнего одуванчика.
Примеры
Входные данные
3 1 1 100 00:01
Выходные данные
01:08
Выбрано
:
|