Создатели модного гаджета iDishwasher (обычная посудомоечная машина с нарисованной на ней надкусанной грушей и продающаяся по баснословной цене) решили добавить в стандартную прошивку игру, которая поможет развлечься домохозяйкам, скучающим во время мытья посуды. Игра похожа на шахматы, правда играют в нее не фигурами, а шахматными клетками. В настольной версии игры дается набор черных и белых полей, из которых необходимо составить квадратную шахматную доску максимального размера. В посудомоечной версии игры дается не набор, а количество полей черного и белого цветов. И в качестве ответа нужно не составить доску, а вывести сторону максимального «шахматного» квадрата, который можно составить из данных клеток. Поскольку не вся целевая аудитория справляется с этой интеллектуальной игрой, вам требуется написать программу, которая поможет отчаявшимся пользователям гаджета.

На шахматной доске стоит несколько офицеров и ладей. Требуется посчитать количество свободных клеток, которые не находятся под боем ни одной из фигур.

Замечание для тех, кто не умеет играть в шахматы:

Шахматная доска имеет размеры 8*8. Ладья бьет все клетки горизонтали и вертикали, проходящих через клетку, где она стоит, до первой встретившейся фигуры. Офицер бьет все клетки обеих диагоналей, проходящих через клетку, где он стоит, до первой встретившейся фигуры.

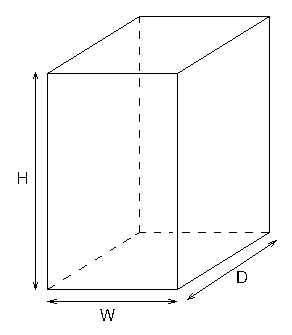
Игра в трехмерный тетрис происходит на поле, имеющем вид прямоугольного параллелепипеда размером W×D×H единичных кубиков. Введем координатную систему так, чтобы один из углов параллелепипеда находится в точке (0, 0, 0), противоположный ему – в точке (W, D, H), а ребра параллелепипеда были параллельны осям координаты. Каждый единичный кубик поля можно задать максимальными координатами его углов, тогда кубики будут иметь координаты от (1, 1, 1) до (W, D, H).

В процессе игры на поле последовательно появляются фигуры. Каждая фигура представляет собой множество единичных кубиков и обладает следующим свойством: от любого кубика можно добраться до любого другого, переходя через общую грань.

Игрок может сделать несколько действий с фигурой. Каждое действие является либо перемещением ее на один в направлении одной из осей координат, либо поворотом ее на 90 градусов вокруг одной из координатных осей. Один из кубиков в фигуре является базовым – при поворотах он остается на месте. При повороте фигура сначала исчезает с игрового поля, и затем появляется снова, уже в новом положении. Направления поворотов показаны на рисунке, при повороте вокруг оси OX ось OY переходит в ось OZ, при повороте вокруг оси OY ось OZ переходит в ось OX, при повороте вокруг оси OZ ось OX переходит в ось OY. Базовый кубик при повороте остается на месте.

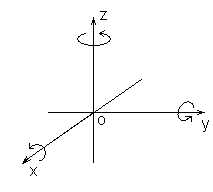Требуется написать программу модуля, ответственного за определение кубиков, которые в результате игры окажутся заняты фигурами. Заранее известна последовательность появления фигур на поле и действия с этими фигурами, которые произвел игрок. Гарантируется, что каждое из действий допустимо, то есть не происходит выхода фигуры за границу поля, и не происходит появления у двух фигур общего кубика.