Известно, что запись числа A в позиционных системах счисления с основанием p и q имеет вид бесконечной периодической дроби с периодом 2:

Написать программу, которая для введенных натуральных чисел p и q находит и выводит все возможные пары значений цифр a и b, удовлетворяющих соотношению ( * ).

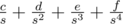
Определим множества K[i] рекуррентно. Пусть K[0] = [0, 1]. Разделим сегмент [0, 1] на три части точками и и удалим из него интервал 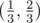. Получим множество K[1], состоящее из двух оставшихся сегментов 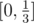и .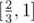

Каждый из них разделим на три части (точками и для первого сегмента, и точками и - для второго) и удалим средние интервалы 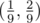и 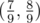. Таким образом получаем множество K[2], и т.д.

Пусть мы построим множество K[i]. Поделим каждый оставшийся сегмент из K[i] на 3 части и удалим из этих сегментов средние интервалы. Получим, таким образом, из K[i] множество K[i + 1].

Вводятся 3 целых числа n, a, b. Необходимо определить, принадлежит ли точка с координатой множеству K[n].

Заданы натуральные числа e, k, m, t в записи химической реакции

Вводятся целые числа a и b. Пусть у треугольника ABC координаты A = (0, 0), B = (a, b), а обе координаты C = (x, y) - целые числа, и площадь треугольника ABC не равна нулю.

Какую минимальную площадь может иметь треугольник ABC?

Имеется n банок с целочисленными объемами V₁, ..., V_n литров, пустой сосуд и кран с водой. Можно ли с помощью этих банок налить в сосуд ровно V литров воды?