Системы счисления(36 задач)
"Длинная" арифметика(58 задач)
Простые числа и разложение на множители(45 задач)
Остатки(21 задач)
Быстрое возведение в степень(3 задач)
Быстрое преобразование Фурье(3 задач)
Многочлен
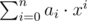
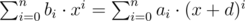
В первой строке даны два целых числа n и d (1 ≤ n ≤ 500, |d| ≤ 2000). Во второй строке даны коэффициенты многочлена a0, ..., an (|ai| ≤ 2000, an ≠ 0).
Выведите n + 1 строку — коэффициенты b0, ..., bn, по одному в каждой строке.
2 -2 21 14 3
5 2 3
Вычислить значение полинома
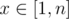 Требуется написать оптимальное решение, то есть нужно использовать не более 3, 001, 000 операций сложения и умножения
Требуется написать оптимальное решение, то есть нужно использовать не более 3, 001, 000 операций сложения и умноженияВ первой строке содержится одно число n (1 ≤ n ≤ 6·105). Во второй строке содержится пять чисел — e, d, c, b, a ( - 100 ≤ a, b, c, d, e ≤ 100).
Выведите n строк — значения полинома f(i), где i — номер строки.
3 5 4 3 2 1
15 57 179
Назовем натуральное число почти простым, если оно раскладывается на произведение каких-нибудь двух неравных простых.
Дано одно натуральное число n ( 2 ≤ n ≤ 2·10 9 ).
Выведите «YES», если n почти простое. Иначе выведите «NO»
10
YES
9
NO
Два юных шамана Егор и Саша отправились на Всероссийский Конкурс Опытных Шаманов Профессионалов. До места проведения ВКОШП можно добраться только на поезде. Всего в вагоне поезда восемь купе по четыре места в каждом. Схема нумерации мест первого купе представлена на рисунке.
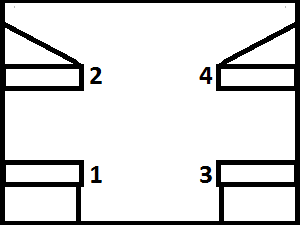
Вам известны номера мест Егора и Саши. В данный момент друзья находятся на перроне и хотят узнать, попадут ли они в одно купе и на каких полках (верхних или нижних) будут ехать.
В единственной строке содержатся два натуральных числа — номера мест Саши и Егора соответственно. Гарантируется, что они не будут превышать количество мест в вагоне, описанном в условии. Также гарантируется, что у Егора и Саши билеты на разные места.
В первой строке выведите "YES", если друзья попадут в одно купе, и "NO" — иначе. Во второй строке выведите "LOW", если Саша будет ехать на нижнем месте, и "HIGH", если на верхнем. В третьей строке выведите положение места Егора в том же формате
В этой задаче всего 50 тестов, каждый оценивается в 2 балла независимо от других.
1 2
YES LOW HIGH
1 5
NO LOW LOW
Несколько школьников решили отпраздновать Новый Год вместе. Для празднования они закупили гору продуктов, и в том числе батон колбасы. Количество еды было настолько велико, что об этом батоне вспомнили только через два с лишним часа после боя курантов. И, конечно, в честь столь знаменательного момента времени школьники решили как можно быстрее съесть этот батон. Но на этом пути их поджидала одна трудность: батон надо разрезать на N (по числу школьников) равных частей, причём как можно быстрее, чтобы не упустить момент. Для этой цели нашёлся очень длинный и острый нож, который смог бы при необходимости разрезать даже N батонов колбасы за один раз. Кроме того, нашлась линейка, с помощью которой можно отмерять любую наперёд заданную часть батона, выбирая место будущего разреза с достаточной точностью. Батон колбасы оказался настолько тонким и длинным, что резать его имело смысл только перпендикулярно его оси.
Конечно, школьники быстро сообразили, что для ускорения процесса можно резать несколько кусков батона одновременно. Батон колбасы оказался прямым и негнущимся, поэтому сэкономить число действий за счёт складывания батона перед разрезанием нельзя. Им осталось определить минимальное количество движений ножом, с помощью которых можно осуществить их намерения. Помогите им в этом. В процессе разрезания школьник может приложить некоторые имеющиеся у него куски батона колбасы друг к другу как он хочет (напомним, что батон очень длинный и тонкий, поэтому имеет смысл прикладывать куски только параллельно друг другу), и одним движением ножа разрезать все куски. Изначально у школьника есть один кусок — сам батон; в конце у него должно быть N одинаковых по длине кусков (каждый длиной в 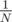 начального батона). Например, разрезать батон на 6 частей (N = 6) школьник может всего за 3 действия ножом:
начального батона). Например, разрезать батон на 6 частей (N = 6) школьник может всего за 3 действия ножом:
 длины всего батона и в этом месте разрезать батон.
длины всего батона и в этом месте разрезать батон. Чтобы разрезать батон на 5 равных частей (N = 5), также необходимо 3 действия ножом, например:
 длины батона и разрезаем батон в этом месте.
длины батона и разрезаем батон в этом месте.  всего батона и один — длиной
всего батона и один — длиной  .
. Во входном файле находится одно число N (1 ≤ N ≤ 2 000 000 000).
Выведите в выходной файл одно число — минимальное количество движений ножом.
6
3
5
3