Системы счисления(36 задач)
"Длинная" арифметика(58 задач)
Простые числа и разложение на множители(45 задач)
Остатки(21 задач)
Быстрое возведение в степень(3 задач)
Быстрое преобразование Фурье(3 задач)
Мы создали бесконечный кроссворд, взяв прямоугольник размера \(\)\(N \times M\)\(\), заполненный буквами и замостили им бесконечную плоскость. Например, прямоугольник
hsin
...hsinhsinhsinhsin...
...honihonihonihoni...
...hsinhsinhsinhsin...
В данном кроссворде нами случайно (равновероятно) выбирается одна клетка и одно из восьми направлений. Затем начиная с данной клетки в данном направлении выписывается слово длины \(\)\(K\)\(\). Описанный процесс повторяется (независимо от первого раза) второй раз. Вам требуется вычислить вероятность того, что два выписанных слова совпадут.
Первая строка содержит три числа \(\)\(M, N, K\)\(\) (\(\)\(1 \leq N, M \leq 500\)\(\), \(\)\(1 \leq K \leq 10^9\)\(\)) — размеры блока и длина выбираемого слова соответственно.
Следующие \(\)\(M\)\(\) строк содержат по \(\)\(N\)\(\) латинских строчных букв, задавая блок, коим замощается доска. Гарантируется, что в данных есть хотя бы две различные буквы.
Выведите требуемую вероятность в виде сокращённой дроби «p/q» без пробелов и кавычек.
Решение, правильно работающее на тестах, в которых \(\)\(N = M\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
1 2 2 ab
5/16
2 4 3 honi hsin
19/512
3 3 10 ban ana nab
2/27
Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.
Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.
Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.
Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)).
В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\)) — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.
Выведите искомое число способов ударить по окну, не задев ни одной мухи.
Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
Пояснение к третьему примеру:
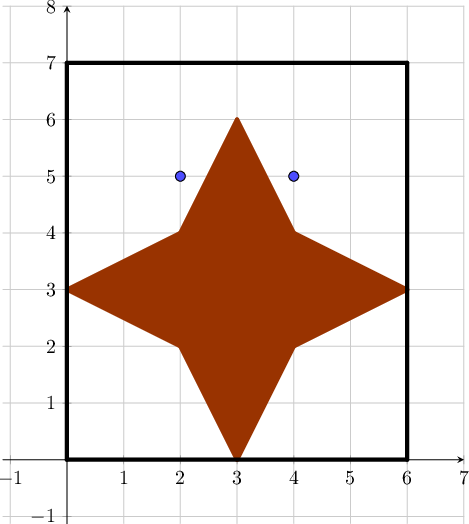
4 5 2 1 3 3 4 4 0 0 2 0 2 2 0 2
4
5 5 3 1 4 1 3 2 2 3 4 7 6 3 7 6
3
6 7 2 2 5 4 5 8 1 4 3 3 4 1 5 3 7 4 5 5 4 7 3 5
1
Рассмотрим следующую операцию, определённую на целых положительных числах. Операция состоит в умножении числа \(q\) на простое число \(p\), либо в делении числа \(q\) на простое число \(p\), если \(q\) делится на \(p\) без остатка. Назовем расстоянием между числами \(a\) и \(b\) минимальное количество операций, необходимое для того чтобы получить из числа \(a\) число \(b\). Обозначим расстояние как \(d(a, b)\).
Дана последовательность из \(n\) положительных чисел \(a_1, a_2, ... a_n\). Для каждого индекса \(i\) (\( 1 \le i \le n\)) необходимо найти индекс \(j\), такой что \(1 \le j \le n\) и \(i \ne j\), и что \(d(a_i, a_j)\) минимально.
Первая строка входных данных содержит одно целое число \(n\) — количество элементов в последовательности \(a\) (\(1 \le n \le 100 000\)).
В последующих \(n\) строках входных данных даны \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) — элементы последовательности (\(1 \le a_i \le 10^{6}\)) (\(i\)-е число в \(i + 1\) строке).
Выведете \(n\) строк. В \(i\) строке выведете такой минимальный индекс \(j\), такой что \(1 \le j \le n\) и \(i \ne j\), и что \(d(a_i, a_j)\) минимально.
В тестах суммарной стоимостью не менее \(30\) баллов дополнительно гарантируется что \(n \le 1000\), \(a_i \le 10000\).
6 1 2 3 4 5 6
2 1 1 2 1 2
2 1 1
2 1
Байтазар планирует заняться производством солнечных панелей. Он получил \(n\) заказов, каждый заказ характеризуется минимальной \(w_{min}\) и максимальной \(w_{max}\) шириной солнечной панели, а также минимальной \(l_{min}\) и максимальной \(l_{max}\) длиной солнечной панели. Выполняя заказ, Байтзар может изготовить солнечную панель любого размера \(a \times b\), такого что \(w_{min} \le a \le w_{max}, l_{min} \le b \le l_{max}\). Солнечная панель состоит из квадратных ячеек. Ячейка может иметь любой размер \(c \times c\), где \(c\) — целое число. Байтазар хотел бы использовать для каждого заказа как можно большие по размеру ячейки. Помогите ему найти для каждого заказа максимальное \(c\), такое что он сможет выполнить заказ, используя ячейки \(c \times c\).
Первая строка ввода содержит число \(n\) (\(1 \le n \le 1000\)) — количество заказов. Следующие \(n\) строк содержит по четыре целых числа \(w_{min}, w_{max}, l_{min}, l_{max}\) и описывают заказы (\(1 \le w_{min} \le w_{max} \le 10^9, 1 \le l_{min} \le l_{max} \le 10^9\) ).
Для каждого заказа выведите одно число: максимальную длину стороны квадратной ячейки, из которых можно изготовить панель для этого заказа.
Подзадача 1 (10 баллов): \(1 \le n \le 10\)
Подзадача 2 (40 баллов): \(1 \le l_{max}, w_{max} \le 10 ^ 7\)
Подзадача 3 (50 баллов): Нет дополнительных ограничений. Зависит от подзадач 1 и 2.
4 3 9 8 8 1 10 11 15 4 7 22 23 2 5 19 24
8 7 2 5
Легенда этой задачи слишком велика, чтобы она уместилась на этой странице, поэтому ее здесь не будет.
Вам дан массив \(V\) длины \(n\), и вы хотите уметь осуществлять над ним следующие операции:
1) get(\(a\), \(b\)) - узнать наибольший общий делитель чисел на отрезке от \(a\) до \(b\).
2) update(\(a\), \(b\), \(k\)) - для всех \(j\) от \(a\) до \(b\) увеличить \(j\)-е число на \(k \cdot (j - a + 1)\), т.е.
\(V_a += k\)
\(V_{a+1} += 2 \cdot k\)
...
\(V_b += (b - a + 1) \cdot k\)
Первая строка входного файла содержит два числа \(1 \le n \le 10^5\) - кол-во числе в массиве и \(1 \le q \le 10^5\) - кол-во запросов. Следующая строка содержит \(n\) чисел - массив \(V\) \(1 \le V_i \le 2 \cdot 10^8\).
Далее в \(q\) строках идет информация о запросах:
Каждый запрос get задается тремя числами 0 \(a\) \(b\)
Каждый запрос update задается четырьмя числами 1 \(a\) \(b\) \(k\) (\(1 \le k \le 2 \cdot 10^8\))
Для каждого запроса get выведите наибольший общий делитель чисел на отрезке от \(a\) до \(b\)
Подзадача 1(20 баллов) \(1 \le n \le 1000\), \(1 \le q \le 1000\)
Подзадача 2(20 баллов) нет запросов update
Подзадача 3(60 баллов) нет дополнительных ограничений
8 3 2 8 12 24 66 33 21 7 0 2 4 1 1 4 2 0 2 4
4 2