--->
3 задач
<---
Источники
Страница:
1
Отображать по:
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Дано целое положительное число в десятичной записи. Рассмотрим числа, полученные из него циклическим сдвигом на 0, 1, ..., N - 1 цифр, и каждое из этих N чисел умножим на его первую цифру цифру. Требуется вывести сумму полученных произведений.
Входные данные
На вход подается одна строка, содержащая десятичную запись целого положительного числа, без ведущих нулей, длиной не более 250 000 цифр.
Выходные данные
Выведите одно число — ответ к задаче.
Примеры
Входные данные
22
Выходные данные
88
#113774
ограничение по времени на тест
6.0 second;
ограничение по памяти на тест
512 megabytes
Жюри не гарантирует существование решения, выполняющегося на всех тестах с двукратным запасом времени работы.
Для числа k рассмотрим все такие различные мультимножества положительных чисел, что их сумма в точности k . Например для k = 3 эти множества {1, 1, 1} , {1, 2} , {3} .
Интересностью числа назовем сумму кубов размеров всех различных мультимножеств. Например интересность числа k = 3 равна 3 3 + 2 3 + 1 3 = 27 + 8 + 1 = 36 .
Поскольку задача должна быть интересной, вам нужно посчитать интересность всех чисел от 1 до n по модулю MOD .
Входные данные
В единственной строке входных данных задаются два числа n и MOD ( 1 ≤ n ≤ 10 5 , 1 ≤ MOD ≤ 10 9 + 7 ) — максимальное число, для которого надо посчитать интересность, и модуль.
Модуль не обязательно простой.
Выходные данные
Выведите n строк, в i -й строке должна содержаться интересность числа i по модулю MOD .
Система оценки
Данная задача содержит 8 групп тестов, баллы за группу выставляются только при прохождении всех тестов группы.
- 1 ≤ n ≤ 5 , 5 баллов.
- 1 ≤ n ≤ 10 , 5 баллов.
- 1 ≤ n ≤ 20 , 10 баллов.
- 1 ≤ n ≤ 100 , 10 баллов.
- 1 ≤ n ≤ 1000 , 10 баллов.
- 1 ≤ n ≤ 5000 , 10 баллов.
- 1 ≤ n ≤ 50 000 , 25 баллов.
- 1 ≤ n ≤ 100 000 , 25 баллов.
Примеры
Входные данные
3 998244353
Выходные данные
1 9 36
Входные данные
10 3
Выходные данные
1 0 0 0 2 2 0 2 2 0
#114061
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.
Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.
Входные данные
Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.
Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)).
В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\)) — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.
Выходные данные
Выведите искомое число способов ударить по окну, не задев ни одной мухи.
Система оценки
Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
Примечание
Пояснение к третьему примеру:
Примеры
Входные данные
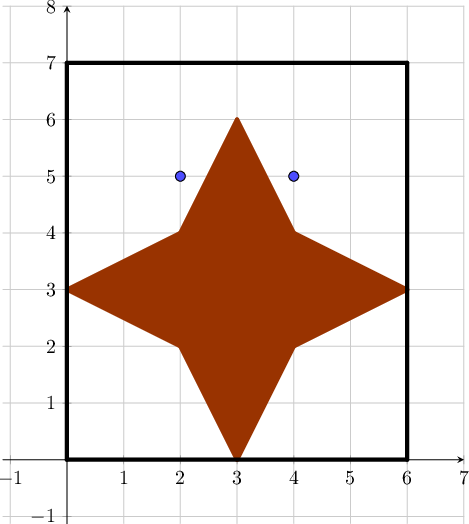
4 5 2 1 3 3 4 4 0 0 2 0 2 2 0 2
Выходные данные
4
Входные данные
5 5 3 1 4 1 3 2 2 3 4 7 6 3 7 6
Выходные данные
3
Входные данные
6 7 2 2 5 4 5 8 1 4 3 3 4 1 5 3 7 4 5 5 4 7 3 5
Выходные данные
1
Страница:
1
Отображать по:
Выбрано
:
|