--->
45 задач
<---
Источники
#1088
Темы:
[НОД и алгоритм Евклида]
[Цикл for]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Петя решил зашифровать свой дневник, чтобы никто без его ведома не смог его прочитать. Для этого он воспользовался следующим шифром.
Он изготовил трафарет NxN клеток (N — четное), в котором вырезал клеток так, что при наложении трафарета на лист бумаги четырьмя возможными способами (трафарет можно поворачивать, но нельзя переворачивать) каждая клетка листа видна ровно один раз.
Пример такого трафарета показан на рисунке ниже:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С помощью этого трафарета шифруется текст из N2 символов следующим образом. Сначала в прорези трафарета вписываются первые букв шифруемого текста (буквы вписываются в вырезанные клетки по строкам сверху вниз, в каждой строке — слева направо). Например, если Петя шифрует слово ОЛИМПИАДА, то оно будет вписано в клетки следующим образом:
| О |
|
|
| Л |
|
|
| И |
| М |
|
|
|
|
|
|
| П |
|
|
|
| И |
|
| А |
| Д |
|
|
|
|
|
|
|
|
| А |
|
|
Далее трафарет поворачивается на 90 градусов по часовой стрелке, и в вырезанные клетки в том же порядке вписываются следующие букв шифруемого текста. И так далее. Если шифруемый текст состоит меньше, чем из N2 символов, то (когда текст кончается) оставшиеся клетки остаются пустыми.
Например, если Петя шифрует текст ОЛИМПИАДА ПО ИНФОРМАТИКЕ 2006 ГОДА при помощи приведенного трафарета, то процесс шифрования будет устроен так. Как зашифровать слово ОЛИМПИАДА, мы уже показали. Для удобства здесь и далее пробел будем обозначать знаком подчеркивания. При втором прикладывании трафарета Пете удастся зашифровать _ПО_ИНФОР:
| О | _ |
|
| Л | П |
|
| И |
| М | О |
|
|
|
| _ |
| П |
|
| И |
| И |
| Н | А |
| Д |
|
| Ф |
| О |
|
|
| Р | А |
|
|
При третьем прикладывании трафарета Петя зашифрует МАТИКЕ_20:
| О | _ | М |
| Л | П |
|
| И |
| М | О | А |
| Т |
| _ | И | П |
|
| И | К | И |
| Н | А |
| Д |
| Е | Ф | _ | О |
|
| 2 | Р | А |
| 0 |
При четвертом прикладывании трафарета Петя зашифрует 06_ГОДА. Остальные клетки окажутся пустыми (будем считать, что в них записан пробел, который мы обозначаем подчеркиванием):
| О | _ | М | 0 | Л | П |
| 6 | И | _ | М | О | А |
| Т | Г | _ | И | П | О |
| И | К | И | Д | Н | А |
| Д | А | Е | Ф | _ | О |
| _ | 2 | Р | А | _ | 0 |
После этого получившийся текст Петя выписывает в строчку:
О М0ЛП6И МОАТГ ИПОИКИДНАДАЕФ О 2РА 0
Для повышения надежности Петя решил зашифрованный текст зашифровать тем же методом с помощью того же трафарета еще раз, затем получившийся текст — еще раз и т.д. После нескольких повторов Петя с удивлением заметил, что зашифрованный текст совпал с исходным.
Напишите программу, которая для данного трафарета определит, после какого наименьшего количества процедур шифрования Петя получит исходный текст независимо от содержания текста?
Входные данные
Сначала во входном файле записано число N — размер трафарета (2≤N≤150). Затем идет N2 чисел (каждое из которых 0 или 1), описывающих трафарет. 1 обозначает вырезанную клетку, 0 — не вырезанную. Гарантируется, что данная последовательность описывает корректный трафарет для данного способа шифрования.
Выходные данные
В выходной файл выведите одно число — через какое минимальное количество повторов операции шифрования Петя получит исходный текст независимо от его содержания.
Примеры
Входные данные
2 1 0 0 0
Выходные данные
2
Входные данные
6 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0
Выходные данные
120
#1133
Темы:
[НОД и алгоритм Евклида]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
«Что наша жизнь? Игра!»
Вася в казино играет в интересную игру.
Сначала он платит вступительный взнос за игру и в обмен на деньги получает право играть. Более того, за уплаченные деньги он сразу получает X очков.
На автомате, в который он играет, есть три кнопки. Когда он нажимает первую, к его очкам добавляется A очков. Когда нажимает вторую — добавляется B. Когда нажимает третью — добавляется C очков.
Ему разрешается сначала несколько раз (или ни разу) нажать третью кнопку, и затем несколько раз (или ни разу) — первую. Нажимать вторую кнопку Васе запрещено.
Если после этого он набрал ровно Y очков, то Вася считается выигравшим, и ему выплачивается премия. Если же Y очков набрать не удается, Вася считается проигравшим, и ничего не получает.
Если Вася выиграл, то считается, что он разгадал одну из волшебных последовательностей нажатий, которые приводят к выигрышу. Он имеет право и дальше играть в эту игру, и искать другие такие последовательности, которые X очков превращают в Y, но ему категорически запрещено использовать одну и ту же выигрышную последовательность более одного раза.
Напишите программу, которая посчитает, сколько различных выигрышных последовательностей существует, то есть сколько раз Вася может выиграть в эту замечательную игру.
Входные данные
Во входном файле записаны числа X, A, B, C, Y. Каждое из этих чисел — целое из диапазона [–109, 109].
Выходные данные
В выходной файл выведите одно число — количество различный выигрышных последовательностей. Если таких последовательностей бесконечно много, выведите –1.
Примеры
Входные данные
0 0 -1 0 1
Выходные данные
0
#1202
Темы:
[Конечные автоматы]
[НОД и алгоритм Евклида]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Окружная олимпиада,
2006,
2 тур,
Задача A
]
#1222
Темы:
[НОД и алгоритм Евклида]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
Московская областная олимпиада,
2007,
Задача B
]
Андрей недавно начал изучать информатику. Одним из первых алгоритмов, который он изучил, был алгоритм Евклида для нахождения наибольшего общего делителя (НОД) двух чисел. Напомним, что наибольшим общим делителем двух чисел a и b называется наибольшее натуральное число x, такое, что и число a, и число b делится на него без остатка.
Алгоритм Евклида заключается в следующем:
1.Пусть a, b — числа, НОД которых надо найти.
2.Если b = 0, то число a — искомый НОД.
3.Если b > a, то необходимо поменять местами числа a и b.
4. Присвоить числу a значение a – b.
5.Вернуться к шагу 2.
Андрей достаточно быстро освоил алгоритм Евклида и вычислил с его помощью много наибольших общих делителей. Поняв, что надо дальше совершенствоваться, ему пришла идея решить новую задачу. Пусть заданы числа a, b, c и d. Требуется узнать, наступит ли в процессе реализации алгоритма Евклида для заданной пары чисел (a, b) такой момент, когда перед исполнением шага 2 число a будет равно c, а число b будет равно d.
Требуется написать программу, которая решает эту задачу.
Входные данные
Первая строка входных данных содержит количество наборов входных данных K (1 ≤ K ≤ 100). Далее идут описания этих наборов. Каждое описание состоит из двух строк. Первая из них содержит два целых числа: a, b (1 ≤ a, b ≤ 1018). Вторая строка – два целых числа: c, d (1 ≤ c, d ≤ 1018).
Все числа в строках разделены пробелом.
Выходные данные
Для каждого набора входных данных выведите слово «YES», если в процессе применения алгоритма Евклида к паре чисел (a, b) в какой-то момент получается пара (c, d). В противном случае выведите слово «NO».
Примеры
Входные данные
2 20 10 10 10 10 7 2 4
Выходные данные
YES NO
#1346
Темы:
[НОД и алгоритм Евклида]
[Элементарная геометрия]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
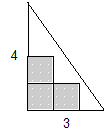Территория Великой Треугольной Области (ВТО) представляет собой прямоугольный треугольник. Длины его катетов равны M и N государственных единиц длины (ГЕД). Правительство ВТО решило покрыть как можно большую часть территории области квадратными плитами размером 11 ГЕД. Плиты должны плотно прилегать друг к другу и к катетам ВТО. Разрезать плиты нельзя.
Согласно межгосударственным соглашениям, правительство ВТО не имеет права покрыть частью своей плиты чужую территорию. Производитель поставляет плиты только контейнерными партиями — по P плит. Правительство заказывает столько контейнеров, сколько необходимо для реализации проекта.
Заведующий центральным складом, узнав про проект, решил, что его интересует количество плит, которые останутся на складе из последнего контейнера после покрытия территории ВТО.
Напишите программу, которая по длинам катетов ВТО и вместимости контейнера находит количество плит, которые останутся на складе после осуществления проекта.
Входные данные
Единственная строка входного файла содержит три целых числа: M, N (2≤M, N≤2 000 000 000) и P (100≤P≤10 000).
Выходные данные
Единственная строка выходного файла должна содержать целое число — количество неиспользованных плит из последнего контейнера.
Примеры
Входные данные
4 3 100
Выходные данные
97
Выбрано
:
|