--->
45 задач
<---
Источники
#3880
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
На досуге вы любите почитать сборники занимательных задач по математике. Недавно вы наткнулись в одном из таких сборников на следующую задачу:
Есть бесконечный резервуар с водой и два пустых сосуда объёмом 5 и 12 литров. Можно наливать воду из резервуара в любой сосуд до его заполнения, переливать воду из —одного сосуда в другой до заполнения второго или опустошения первого (смотря что будет раньше) и выливать воду из сосуда на землю до полного опустошения сосуда. Как таким образом можно отмерить 3 литра?
Вы решили написать программу, которая будет решать подобные задачи для произвольных объёмов сосудов.
Входные данные
Во входном файле находятся три целых числа — \(V_1\), \(V_2\) и \(V\) — объёмы двух сосудов и объем воды, который нужно отмерить. Гарантируется, что \(1\leq V_1,V_2\leq 32767\) и \(0\leq V\leq \max(V_1,V_2)\).
Выходные данные
В первую строку выходного файла выведите одно число — количество действий в вашем решении. Далее выведите соответствующее количество строк, описывающих действия в вашем решении. Для каждого действия выведите два числа:
- если это действие — переливание из одного сосуда в другой, то первое число должно быть номером сосуда, откуда надо переливать воду, а второе — номером сосуда, куда переливать;
- если это действие — набор воды из резервуара, то первое число должно быть нулём, а второе — номером сосуда, куда наливать;
- если это действие — выливание воды “на землю”, то первое число должно быть номером сосуда, а второе — нулём.
После выполнения всех операций хотя бы в одном сосуде должна находиться вода в объёме \(V\).
Если существует несколько решений, то вы можете вывести любое. Ваше решение не обязано быть оптимальным, единственное ограничение — размер выходного файла не должен превосходить 3 Мб.
Если решений не существует, выведите одно число -1.
Примеры
Входные данные
5 12 3
Выходные данные
10 0 1 1 2 2 1 1 2 0 1 1 0 0 1 1 2 0 1 1 2
#3887
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
В городе N строят метро. Вася, житель города N, хочет знать, сколько станций окажутся недалеко от его дома. Помогите ему.
Город N отличается очень строгой планировкой улиц: каждая улица идёт либо строго с юга на север, либо строго с востока на запад; при этом расстояние между соседними параллельными улицами одинаково. Соответственно, в городе есть много перекрёстков, расположенных в вершинах квадратной сетки. По планам, первая линия метро будет прямой и будет иметь станции на каждом перекрёстке, через который она пройдёт. Вася считает, что станция находится недалеко от его дома, если расстояние по прямой от его дома до станции не превосходит некоторой фиксированной величины \(R\).
Входные данные
Введём систему координат с осью \(x\), направленной с востока на запад, и осью \(y\), направленной с юга на север, с началом координат на одном из перекрёстков и с единицей длины, равной расстоянию между соседними параллельными улицами. Таким образом, улицы будут прямыми с уравнениями ..., \(x=-2\), \(x=-1\), \(x=0\), \(x=1\), \(x=2\), ..., а также ..., \(y=-2\), \(y=-1\), \(y=0\), \(y=1\), \(y=2\), ...
Во первой строке входного файла находятся целые числа \(x_0\), \(y_0\) — координаты Васиного дома (считаем, что он находится на некотором перекрёстке), — и расстояние \(R\) в тех же единицах измерения, в которых введены координаты. Во второй строке находятся четыре числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты некоторых двух различных перекрёстков, через которые пройдёт линия метро. Все координаты во входном файле не превосходят \(100\,000\,000\) по модулю; расстояние \(R\) целое, положительное и не превосходит \(100\,000\,000\).
Можете считать, что линия метро будет бесконечной в обоих направлениях.
Выходные данные
В выходной файл выведите одно число — количество станций, расположенных недалеко от Васиного дома.
Примечание
Первый пример соответствует рисунку; на рисунке дом Васи и станции метро обозначены жирными
точками.
Примеры
Входные данные
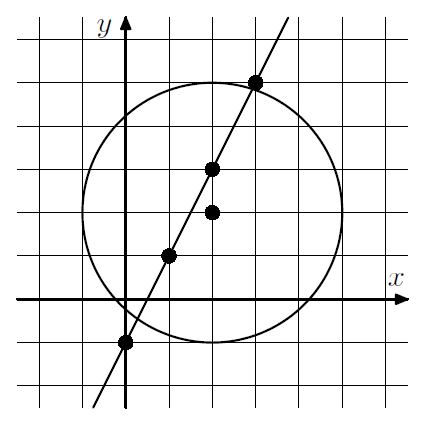
2 2 3 0 -1 1 1
Выходные данные
2
Входные данные
0 0 1 -5 0 -3 0
Выходные данные
3
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Даны натуральные числа \(a\), \(b\), \(c\). Если уравнение \(ax+by=c\) имеет
решения в целых числах, то выберите то решение, в котором число \(x\) имеет
наименьшее неотрицательное значение и выведите это решение (два числа \(x\) и \(y\) через один пробел).
Если решения не существует, то выведите слово Impossible.
Входные данные
Вводятся три натуральных числа.
Выходные данные
Выведите ответ на задачу.
Примечание
Сложность алгоритма должна быть равна сложности алгоритма Евклида + константа.
Примеры
Входные данные
1 2 3
Выходные данные
1 1
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дано натуральное число \(n \le 10^8\). Подсчитайте количество таких пар чисел \((a, b)\), что:
- \(a\) и \(b\) — делители \(n\).
- \(a < b\).
- \(a\) и \(b\) — взаимно простые.
- \(ab\le n\).
Входные данные
Вводится натуральное число.
Выходные данные
Выведите количество таких пар.
Примеры
Входные данные
10
Выходные данные
4
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Найдите НОД двух чисел.
Входные данные
Вводятся два натуральных числа, не превосходящих 10 000, разделенные пробелом.
Выходные данные
Выведите одно число - их наибольший общий делитель.
Примеры
Входные данные
2 4
Выходные данные
2
Выбрано
:
|