Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Во время недавних раскопок на Марсе были обнаружены листы бумаги с таинственными символами на них. После долгих исследований учёные пришли к выводу, что надписи на них на самом деле могли быть обычными числовыми равенствами. Если бы этот вывод оказался верным, это доказало бы не только то, что на Марсе много лет назад были разумные существа, но и то, что они уже умели считать…
Ученые смогли понять, что в этом случае означают найденные символы, и перевели эти равенства на обычный язык – язык цифр, скобок, знаков арифметических действий и равенства. Кроме того, из других источников было получено веское доказательство того, что марсиане знали только три операции – сложение, умножение и вычитание (марсиане никогда не использовали «унарный минус»: вместо «-5» они писали «0-5»). Также ученые доказали, что марсиане не наделяли операции разным приоритетом, а просто вычисляли выражения (если в них не было скобок) слева направо: например, 3+3*5 у них равнялось 30, а не 18.
К сожалению, символы арифметических действий марсиане почему-то наносили специальными чернилами, которые, как оказалось, были не очень стойкими, и поэтому в найденных листках между числами вместо знаков действий были пробелы. Если вся вышеизложенная теория верна, то вместо этих пробелов можно поставить знаки сложения, вычитания и умножения так, чтобы равенства стали верными. Например, если был найден лист бумаги с надписью «18=7 (5 3) 2», то возможна такая расстановка знаков: «18=7+(5-3)*2» (помните про то, в каком порядке марсиане вычисляют выражения!). В то же время, если попался лист с надписью «5=3 3», то марсиане явно не имели в виду числового равенства, когда писали это…
Вы должны написать программу, находящую требуемую расстановку знаков или сообщающую, что таковой не существует.
Первая строка входного файла состоит из натурального (целого положительного) числа, не превосходящего 230, знака равенства, и последовательности натуральных чисел (не более десяти), произведение которых также не превосходит 230. Некоторые группы чисел (одно или более) могут быть окружены скобками. Длина входной строки не будет превосходить 80 символов, и других ограничений на количество и вложенность скобок нет. Между двумя соседними числами, не разделенными скобками, всегда будет хотя бы один пробел, во всех остальных местах может быть любое (в том числе и 0) число пробелов (естественно, внутри числа пробелов нет).
В выходной файл необходимо вывести одну строку, содержащую полученное равенство (т.е., исходное равенство со вставленными знаками арифметических действий). В случае если требуемая расстановка знаков невозможна, вывести строку, состоящую из единственного числа \(-1\). Выходная строка не должна содержать пробелов.
Пример ответа для первого теста (ответ 1 - неправильный): 18=7+(5-3)*2
Пример ответа для второго теста (ответ 0 - неправильный): -1
18 = 7 (5 3) 2
1
5 = 3 3
0
Склад конторы MacroHard представляет собой прямоугольную комнату размером NxM. На складе нарисована разметка, состоящая из линий, параллельных стенам склада, которые разбивают его на NxM квадратов 1x1.
Фирма выпускает высокотехнологичное оборудование, используемое в самых различных областях жизнедеятельности. Исторически сложилось так, что все изделия, выпускаемые этой компанией, имеют форму равнобедренного прямоугольного треугольника. При этом ассортимент изделий столь велик, что бывают изделия практически любых размеров.
Размещать изделия на складе разрешается только так, чтобы хотя бы одна сторона изделия была параллельна какой-то из стен склада, и, вдобавок, все углы изделия находились в точках пересечения линий разметки склада. Рисунки 1,2,3 иллюстрируют неправильное положение изделий, а 4,5 – правильное.
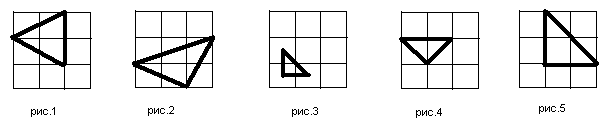
Руководство фирмы узнало, что склад планирует посетить Комиссия по неэффективному использованию складских помещений. Чтобы избежать выплаты крупного штрафа, фирма решила в срочном порядке поместить на склад изделия так, чтобы на складе не осталось свободного места. При этом было решено, что продукция, которая уже находится на складе, перемещаться не будет.
Напишите программу, которая определит, какое минимальное количество изделий можно добавить на склад, чтобы на нем не осталось свободного места.
В первой строке входного файла записаны три целых числа: N, M (размеры склада) и K (количество изделий, которые уже находятся на складе). Следующие K строк содержат по 6 целых чисел — координаты углов соответствующего изделия. Система координат введена так, что оси координат параллельны стенам склада и при этом один из углов склада имеет координаты (0,0), а противоположный — (N,M).
Ограничения
1N4, 1M4
Первая строка выходного файла должна содержать одно число T — минимальное количество изделий, которые необходимо добавить, чтобы полностью заполнить склад. Каждая из следующих T строк должна содержать по 6 чисел — координаты углов изделий.
3 2 0
5 0 0 0 2 2 0 0 2 2 0 2 2 2 0 2 2 3 1 2 0 3 0 3 1 2 2 3 1 3 2
В связи с проведением межпланетного шашечного турнира было принято решение о строительстве орбитальной гостиницы. Она должна была представлять собой большой куб из N×N×N блоков – маленьких кубиков 1×1×1, и каждый блок должен был быть окрашен снаружи со всех сторон в какой-то один цвет. При этом некоторые блоки могли быть покрашены в один и тот же цвет.
Через год были сделаны фотографии гостиницы с каждой из 6 сторон: спереди, слева, сзади, справа, сверху, снизу. За год эксплуатации могло случиться так, что из-за непрочного крепления некоторые блоки, из которых была построена гостиница, оторвались и улетели в открытый космос. Комиссия по восстановлению гостиницы хочет по сделанным снимкам установить максимальное возможное количество оставшихся блоков.
Итак, вам необходимо по видам гостиницы (куба N×N×N, из которого, возможно, выкинуты некоторые кубики 1×1×1) с 6 сторон определить, из какого максимального количества блоков 1×1×1 она может состоять. Может оказаться так, что гостиница состоит из двух или более не связанных между собой частей.
В первой строке входного файла находится число N — размер гостиницы (1≤N≤10). На следующих N строках записаны виды гостиницы с 6 сторон (в следующем порядке: спереди, слева, сзади, справа, сверху, снизу). Каждый такой вид представляет собой таблицу N×N, в которой различными заглавными латинскими буквами обозначены различные цвета, а символом «.» (точка) — то, что в этом месте можно будет смотреть прямо сквозь гостиницу. Два последовательных вида отделяются друг от друга ровно одним пробелом в каждой из N строк.
Нижняя граница вида сверху соответствует верхней границе вида спереди, а верхняя граница вида снизу — нижней границе вида спереди. Для видов спереди, сзади и с боков верх и низ вида соответствуют верху и низу гостиницы.
Входные данные корректны, то есть во входном файле описано состояние, которое может получиться.
Выведите в выходной файл одно число — искомое максимальное количество оставшихся блоков в гостинице.
3 .R. YYR .Y. RYY .Y. .R. GRB YGR BYG RBY GYB GRB .R. YRR .Y. RRY .R. .Y.
11
2 ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ
8
Бригада скорой помощи выехала по вызову в один из отделенных районов. К сожалению, когда диспетчер получил вызов, он успел записать только адрес дома и номер квартиры K1, а затем связь прервалась. Однако он вспомнил, что по этому же адресу дома некоторое время назад скорая помощь выезжала в квартиру K2, которая расположена в подъезда P2 на этаже N2. Известно, что в доме M этажей и количество квартир на каждой лестничной площадке одинаково. Напишите программу, которая вычилсяет номер подъезда P1 и номер этажа N1 квартиры K1.
Во входном файле записаны пять положительных целых чисел K1, M, K2, P2, N2. Все числа не превосходят 1000.
Выведите два числа P1 и N1. Если входные данные не позволяют однозначно определить P1 или N1, вместо соответствующего числа напечатайте 0. Если входные данные противоречивы, напечатайте два числа –1 (минус один).
89 20 41 1 11
2 3
11 1 1 1 1
0 1
3 2 2 2 1
-1 -1